Add chapter about complex numbers
This commit is contained in:
parent
b570a6f958
commit
3bfb6d2400
6 changed files with 177 additions and 0 deletions
Notes/Semester 3/HM1 - Höhere Mathematik
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/ComplexNumberMath.png
Normal file
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/ComplexNumberMath.png
Normal file
Binary file not shown.
|
After 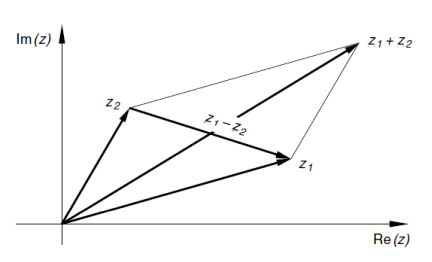
(image error) Size: 21 KiB |
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/ComplexNumbers.png
Normal file
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/ComplexNumbers.png
Normal file
Binary file not shown.
|
After 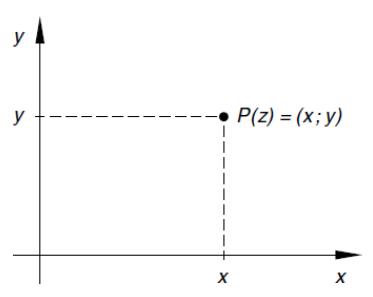
(image error) Size: 8.5 KiB |
Binary file not shown.
|
After 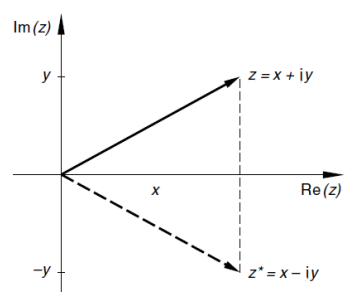
(image error) Size: 15 KiB |
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/RootComplexNumber.png
Normal file
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/RootComplexNumber.png
Normal file
Binary file not shown.
|
After 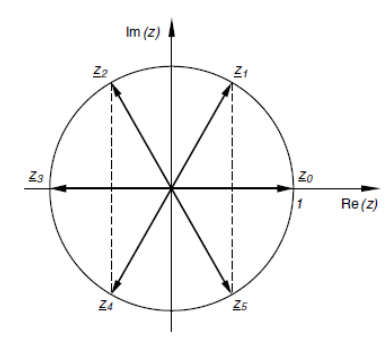
(image error) Size: 26 KiB |
Binary file not shown.
|
After 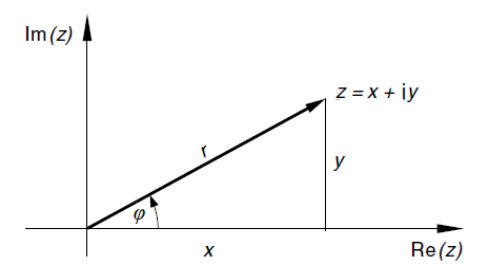
(image error) Size: 15 KiB |
|
|
@ -64,6 +64,8 @@
|
||||||
- [Jacobi-Verfahren](#jacobi-verfahren)
|
- [Jacobi-Verfahren](#jacobi-verfahren)
|
||||||
- [Gauss-Seidel-Verfahren](#gauss-seidel-verfahren)
|
- [Gauss-Seidel-Verfahren](#gauss-seidel-verfahren)
|
||||||
- [Konvergenz](#konvergenz)
|
- [Konvergenz](#konvergenz)
|
||||||
|
- [Komplexe Zahlen](#komplexe-zahlen)
|
||||||
|
- [Rechen-Regeln](#rechen-regeln)
|
||||||
- [Formelbuchstaben](#formelbuchstaben)
|
- [Formelbuchstaben](#formelbuchstaben)
|
||||||
- [Glossar](#glossar)
|
- [Glossar](#glossar)
|
||||||
|
|
||||||
|
|
@ -1213,6 +1215,179 @@ Für alle Matrizen, die diagonal-dominant sind gilt, dass sie für das Jacobi- u
|
||||||
|
|
||||||
</div>
|
</div>
|
||||||
|
|
||||||
|
## Komplexe Zahlen
|
||||||
|
Der Bereich der Komplexen Zahlen dient dazu, Werte abzubilden, die es eigentlich nicht geben kann.
|
||||||
|
|
||||||
|
Beispiel einer komplexen Zahl:
|
||||||
|
|
||||||
|
$$x^2 = -1$$
|
||||||
|
|
||||||
|
Es gibt keinen Wert, der $-1$ ergibt, wenn er quadriert wird. Es handelt sich also um eine komplexe Zahl.
|
||||||
|
|
||||||
|
Dafür wird die imaginäre Einheit $i$ eingeführt mit folgender Eigenschaft:
|
||||||
|
|
||||||
|
$$i^2 = -1$$
|
||||||
|
|
||||||
|
Für diese Definition wäre das Resultat von $x^2= -1$ also $x = \plusmn{i}$
|
||||||
|
|
||||||
|
In Python und in der Elektrotechnik wird der Buchstabe $j$ verwendet.
|
||||||
|
|
||||||
|
Komplexe Zahlen $z$ mit $z = x + i \cdot y$ können nicht auf einem Zahlenstrahl dargestellt werden.
|
||||||
|
|
||||||
|
Sie können in einem Koordinaten-System eingezeichnet werden, wobei $x$ der reale und $y$ der imaginäre Anteil sind:
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
Dieses Koordinaten-System nennt sich auch **Gaussche Zahlenebene**.
|
||||||
|
|
||||||
|
<div class="formula">
|
||||||
|
|
||||||
|
***Komplexe Zahlen:***
|
||||||
|
|
||||||
|
Imaginäre Einheit $i$:
|
||||||
|
|
||||||
|
$$i^2 = -1$$
|
||||||
|
|
||||||
|
Komplexe Zahlen $z$:
|
||||||
|
|
||||||
|
$$z = x + i \cdot y$$
|
||||||
|
|
||||||
|
**Konjugierte** komplexe Zahl:
|
||||||
|
|
||||||
|
$$z^* = x - i \cdot y$$
|
||||||
|
|
||||||
|
Betrag von $z$:
|
||||||
|
|
||||||
|
$$|z| = \sqrt{x^2 + y^2}$$
|
||||||
|
|
||||||
|
Menge aller komplexen Zahlen $\mathbb{C}$:
|
||||||
|
|
||||||
|
$$\mathbb{C} = \{ z | z = x + i \cdot y \text{ mit } x, y \in \mathbb{R}\}$$
|
||||||
|
|
||||||
|
</div>
|
||||||
|
|
||||||
|
Veranschaulichung einer konjugierten komplexen Zahl $z^*$:
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
<div class="letters">
|
||||||
|
|
||||||
|
- $\mathbb{C}$: Menge aller komplexen Zahlen
|
||||||
|
- $x$: Realteil einer komplexen Zahl
|
||||||
|
- $y$: Imaginärteil einer komplexen Zahl
|
||||||
|
- $z$: Komplexe Zahl
|
||||||
|
|
||||||
|
</div>
|
||||||
|
|
||||||
|
<div class="formula">
|
||||||
|
|
||||||
|
***Darstellungsformen:***
|
||||||
|
|
||||||
|
Es gibt diverse Darstellungsformen für komplexe Zahlen:
|
||||||
|
|
||||||
|
- Normalform (auch "algebraische" oder "kartesische" Form):
|
||||||
|
$$z = x + i \cdot y$$
|
||||||
|
- Trigonometrische Form:
|
||||||
|
$$z = r \cdot (\cos(\varphi) + i \cdot \sin(\varphi))$$
|
||||||
|
- Exponential-Form:
|
||||||
|
$$z = re^{i \cdot \varphi}$$
|
||||||
|
|
||||||
|
</div>
|
||||||
|
|
||||||
|
Beispiel einer komplexen Zahl $z$ in der Normalform und der Trigonometrischen Form:
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
<div class="letters">
|
||||||
|
|
||||||
|
- $r$: Die Länge des Vektors einer komplexen Zahl $z$ ($r = |z|$)
|
||||||
|
- $\varphi$: Der Winkel zwischen der x-Achse und dem Vektor der komplexen Zahl $z$
|
||||||
|
|
||||||
|
</div>
|
||||||
|
|
||||||
|
### Rechen-Regeln
|
||||||
|
|
||||||
|
<div class="formula">
|
||||||
|
|
||||||
|
***Rechen-Regeln für komplexe Zahlen:***
|
||||||
|
|
||||||
|
Addition:
|
||||||
|
|
||||||
|
$$z_1 + z_2 = (x_1 + x_2) + i \cdot (y_1 + y_2)$$
|
||||||
|
|
||||||
|
Subtraktion:
|
||||||
|
|
||||||
|
$$z_1 - z_2 = (x_1 - x_2) + i \cdot (y_1 - y_2)$$
|
||||||
|
|
||||||
|
Multiplikation:
|
||||||
|
|
||||||
|
$$z_1 \cdot z_2 = (x_1 \cdot x_2 - y_1 \cdot y_2) +
|
||||||
|
i \cdot(x_1 \cdot y_2 + x_2 \cdot y_2)$$
|
||||||
|
|
||||||
|
Division:
|
||||||
|
|
||||||
|
$$\begin{aligned}
|
||||||
|
\frac{z_1}{z_2} &=
|
||||||
|
\frac{z_1 \cdot z_2^*}{z_2 \cdot z_2^*} =
|
||||||
|
\frac{(x_1 + i \cdot y_1) \cdot (x_2 - i \cdot y_2)}{(x_2 + i \cdot y_2) \cdot (x_2 - i \cdot y_2)} \\
|
||||||
|
&= \frac{(x_1 \cdot x_2 + y_1 \cdot y_2) + i \cdot (y_1 \cdot x_2 - x_1 \cdot y_2)}{x_2^2 + y_2^2} \\
|
||||||
|
&= \frac{(x_1 \cdot x_2 + y_1 \cdot y_2)}{x_2^2 + y_2^2} + i \cdot \frac{(y_1 \cdot x_2 - x_1 \cdot y_2)}{x_2^2 + y_2^2}
|
||||||
|
\end{aligned}$$
|
||||||
|
|
||||||
|
</div>
|
||||||
|
|
||||||
|
Visualisierung von Addition und Subtraktion zwei komplexer Zahlen $z_1$ und $z_2$:
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
<div class="formula">
|
||||||
|
|
||||||
|
***Potenzieren in der Polarform:***
|
||||||
|
|
||||||
|
Für komplexe Zahlen in der Normalform gilt folgendes:
|
||||||
|
|
||||||
|
- Sei $n \in \mathbb{N}$:
|
||||||
|
$$z^n = (r \cdot e^{i \cdot \varphi})^n = r^n \cdot e^{i \cdot n \cdot \varphi} =
|
||||||
|
r^n \cdot (\cos(n \cdot \varphi) + i \cdot \sin(n \cdot \varphi))$$
|
||||||
|
|
||||||
|
</div>
|
||||||
|
|
||||||
|
<div class="formula">
|
||||||
|
|
||||||
|
***Fundamentalsatz der Algebra:***
|
||||||
|
|
||||||
|
Eine algebraische Gleichung $n$-ten Grades mit komplexen Koeffizienten und Variablen $a_i, z \in \mathbb{C}$
|
||||||
|
|
||||||
|
$$a_n \cdot z^n + a_{n - 1} \cdot z^{n - 1} + \dots + a_1 \cdot z + a_0 = 0$$
|
||||||
|
|
||||||
|
besitzt in der Menge $\mathbb{C}$ der komplexen Zahlen genau $n$ Lösungen.
|
||||||
|
|
||||||
|
</div>
|
||||||
|
|
||||||
|
<div class="formula">
|
||||||
|
|
||||||
|
***Ziehen der Wurzel einer komplexen Zahl:***
|
||||||
|
|
||||||
|
Die Gleichung für das Ziehen einer Wurzel $n$ der komplexen Zahl $a$ lautet: $z^n = a$.
|
||||||
|
|
||||||
|
Für die Lösung dieser Gleichung existieren genau $n$ verschiedene Lösungen in der Menge $\mathbb{C}$:
|
||||||
|
|
||||||
|
$$z_k = r \cdot (\cos(\varphi_k + i \cdot \sin(\varphi_k)) = r \dot e^{i \cdot \varphi_k}$$
|
||||||
|
|
||||||
|
für $k = 0, 1, 2, \dots, n - 1$:
|
||||||
|
mit
|
||||||
|
|
||||||
|
$$r = \sqrt[n]{r_0}$$
|
||||||
|
$$\varphi_k = \frac{\varphi + k \cdot 2 \cdot \pi}{n}$$
|
||||||
|
|
||||||
|
Die Bildpunkte der Ergebnisse liegen in der komplexen Zahlenebene auf einem Kreis um den Nullpunkt mit dem Radius $r = \sqrt[n]{r_0}$ und bilden die Ecken eines regelmässigen $n$-Ecks.
|
||||||
|
|
||||||
|
</div>
|
||||||
|
|
||||||
|
Visualisierung des Ziehens der $6$-ten Wurzel einer komplexen Zahl $z$:
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
## Formelbuchstaben
|
## Formelbuchstaben
|
||||||
<div class="letters">
|
<div class="letters">
|
||||||
|
|
||||||
|
|
@ -1226,6 +1401,8 @@ Für alle Matrizen, die diagonal-dominant sind gilt, dass sie für das Jacobi- u
|
||||||
- $e$: Exponent der Maschinenzahl
|
- $e$: Exponent der Maschinenzahl
|
||||||
- $H$: Housholder-Matrix (siehe $QR$-Zerlegung)
|
- $H$: Housholder-Matrix (siehe $QR$-Zerlegung)
|
||||||
- $I$: Identitäts-Matrix (Matrix, überall den Wert $0$ und auf der Diagonalen den Wert $1$ hat)
|
- $I$: Identitäts-Matrix (Matrix, überall den Wert $0$ und auf der Diagonalen den Wert $1$ hat)
|
||||||
|
- $i$: Imaginäre Einheit für die Darstellung komplexer Zahlen
|
||||||
|
- $j$: Alternative Schreibweise für $i$ in Python und in der Elektrotechnik
|
||||||
- $K$: Konditionszahl
|
- $K$: Konditionszahl
|
||||||
- $L$: Untere Dreiecksmatrix/Normierte Matrix
|
- $L$: Untere Dreiecksmatrix/Normierte Matrix
|
||||||
- $m$: Mantisse (Darstellbarer Bereich der Maschinenzahl)
|
- $m$: Mantisse (Darstellbarer Bereich der Maschinenzahl)
|
||||||
|
|
|
||||||
Loading…
Reference in a new issue