Add illustrations
This commit is contained in:
parent
318198177c
commit
5f4cc5e678
4 changed files with 8 additions and 0 deletions
Notes/Semester 3/HM1 - Höhere Mathematik
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/FixedPointIteration.png
Normal file
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/FixedPointIteration.png
Normal file
Binary file not shown.
|
After 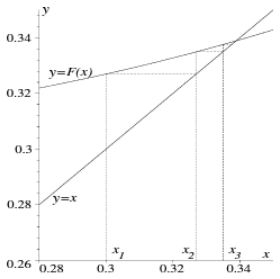
(image error) Size: 18 KiB |
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/NewtonMethod.png
Normal file
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/NewtonMethod.png
Normal file
Binary file not shown.
|
After 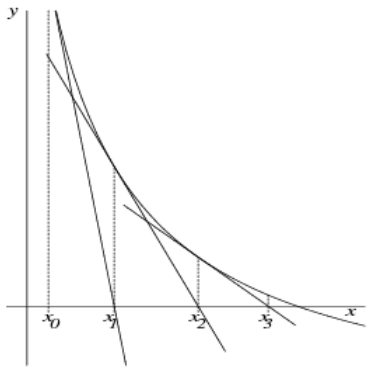
(image error) Size: 24 KiB |
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/SecantMethod.png
Normal file
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/SecantMethod.png
Normal file
Binary file not shown.
|
After 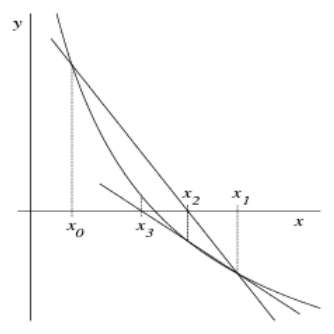
(image error) Size: 18 KiB |
|
|
@ -192,6 +192,9 @@ Es wird der korrekte Wert $x$ für eine Aufgabe gesucht.
|
||||||
> - Ein Threshold von $0$ ergibt das genaue Resultat
|
> - Ein Threshold von $0$ ergibt das genaue Resultat
|
||||||
|
|
||||||
### Fixpunktiteration
|
### Fixpunktiteration
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
Ein möglicher Ansatz für ein solches Problem ist eine Fixpunktiteration.
|
Ein möglicher Ansatz für ein solches Problem ist eine Fixpunktiteration.
|
||||||
|
|
||||||
Der Vorgang für eine solche ist folgende:
|
Der Vorgang für eine solche ist folgende:
|
||||||
|
|
@ -309,6 +312,9 @@ Folgendermassen kann dieser aufgestellt werden:
|
||||||
4. Die a-priori und die a-posteriori Abschätzung kann nun beliebig angewendet werden. Hierbei wird für $x_0$ der Wert $a$ verwendet.
|
4. Die a-priori und die a-posteriori Abschätzung kann nun beliebig angewendet werden. Hierbei wird für $x_0$ der Wert $a$ verwendet.
|
||||||
|
|
||||||
### Newton-Verfahren
|
### Newton-Verfahren
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
Das Newton-Verfahren erreicht die Konvergenz (d.h. das (approximierte) Resultat) um einiges schneller.
|
Das Newton-Verfahren erreicht die Konvergenz (d.h. das (approximierte) Resultat) um einiges schneller.
|
||||||
|
|
||||||
Hierfür wird die Funktion $f$ in der Nullstellenform benötigt ($f(x) = \text{[...]} = 0$).
|
Hierfür wird die Funktion $f$ in der Nullstellenform benötigt ($f(x) = \text{[...]} = 0$).
|
||||||
|
|
@ -342,6 +348,8 @@ Das Ergebnis ist wahr, wenn mit dem gewählten $x$ eine Konvergenz erreicht werd
|
||||||
|
|
||||||
### Sekantenverfahren
|
### Sekantenverfahren
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
<div class="formula">
|
<div class="formula">
|
||||||
|
|
||||||
$$x_{n + 1} = x_n - \frac{x_n - x_{n - 1}}{f(x_n) - f(x_{n - 1})} \cdot f(x_n)$$
|
$$x_{n + 1} = x_n - \frac{x_n - x_{n - 1}}{f(x_n) - f(x_{n - 1})} \cdot f(x_n)$$
|
||||||
|
|
|
||||||
Loading…
Reference in a new issue