Add summary about $QR$-decomposition
This commit is contained in:
parent
5965f0e783
commit
ddf2fcbd36
2 changed files with 166 additions and 0 deletions
Notes/Semester 3/HM1 - Höhere Mathematik
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/ExpandHouseholder.png
Normal file
BIN
Notes/Semester 3/HM1 - Höhere Mathematik/ExpandHouseholder.png
Normal file
Binary file not shown.
|
After 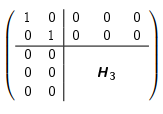
(image error) Size: 3.1 KiB |
|
|
@ -5,6 +5,7 @@
|
|||
color: black;
|
||||
padding: 0.5rem;
|
||||
padding-bottom: 1px;
|
||||
margin-bottom: 0.5rem;
|
||||
}
|
||||
|
||||
.formula p:last-child, .letters p:last-child {
|
||||
|
|
@ -52,6 +53,9 @@
|
|||
- [Fehlerfortpflanzung und Pivotisierung](#fehlerfortpflanzung-und-pivotisierung)
|
||||
- [Determinanten-Bestimmung](#determinanten-bestimmung)
|
||||
- [Die $LR$-Zerlegung](#die-lr-zerlegung)
|
||||
- [$QR$-Zerlegung](#qr-zerlegung)
|
||||
- [Housholder-Matrizen](#housholder-matrizen)
|
||||
- [Vorgang](#vorgang)
|
||||
- [Formelbuchstaben](#formelbuchstaben)
|
||||
- [Glossar](#glossar)
|
||||
|
||||
|
|
@ -721,6 +725,164 @@ Wenn die $LR$-Zerlegung, wie in diesem Code, Zeilenaustausch und das Berechnen v
|
|||
2. Mit Hilfe des Gauss-Algorithmus $L \cdot y = P \cdot b$ nach $y$ auflösen
|
||||
3. Mit Hilfe des Gauss-Algorithmus $R \cdot x = y$ nach $x$ auflösen
|
||||
|
||||
### $QR$-Zerlegung
|
||||
|
||||
- Die Matrix $A$ wird in eine orthogonale Matrix $Q$ und eine obere Dreiecksmatrix $R$ zerlegt.
|
||||
- Orthogonal-Matrizen beschreiben Drehungen, Spiegelungen oder Kombinationen daraus.
|
||||
- Eine $QR$-Zerlegung erfordert ca. $\frac{5}{3}n^3$ Punktoperationen - ca. doppelt so viel wie die $LR$-Zerlegung.
|
||||
|
||||
<div class="formula">
|
||||
|
||||
***Orthogonal-Matrix:***
|
||||
|
||||
Eine Matrix $Q$ ist orthogonal, wenn folgendes gilt:
|
||||
|
||||
$$Q^T \cdot Q = I_n$$
|
||||
|
||||
($x^T$ steht hierbei für eine **T**ransformation)
|
||||
|
||||
</div>
|
||||
|
||||
#### Housholder-Matrizen
|
||||
|
||||
Im Rahmen der Berechnung der Matrizen $Q$ und $R$ werden sogenannte "Housholder-Matrizen" berechnet.
|
||||
|
||||
<div class="formula">
|
||||
|
||||
***Housholder-Matrizen:***
|
||||
|
||||
Sei $u$ ein Vektor mit beliebig vielen Dimensionen, für den gilt:
|
||||
|
||||
$$|u| = \sqrt{u_1^2 + u_2^2 + \dots + u_n^2} = 1$$
|
||||
|
||||
Die Householder-Matrix hat folgende Eigenschaft:
|
||||
|
||||
$$H := I_n - 2 \cdot u \cdot u^T$$
|
||||
|
||||
Für Housholder-Matrizen gilt zudem folgendes:
|
||||
|
||||
$$H = H^T = H^{-1}$$
|
||||
|
||||
und
|
||||
|
||||
$$H \cdot H = I_n$$
|
||||
|
||||
</div>
|
||||
|
||||
***Berechnung einer Housholder-Matrix***
|
||||
|
||||
Beispiel der Berechnung einer Housholder-Matrix zur ersten Spalte der Matrix $A$.
|
||||
|
||||
> Für die Berechnung wird ein Einheitsvektor $e$ benötigt, welcher genauso viele Werte hat, wie die Matrix Dimensionen. Ein Einheitsvektor hat im ersten Feld den Wert $1$ und in allen anderen Feldern der Wert $0$.
|
||||
>
|
||||
> Für eine Matrix $A$ mit der Dimension $n = 3$ lautet der Einheitsvektor $e$ also wie folgt:
|
||||
> $$e = \left(\begin{matrix}
|
||||
> 1 \\
|
||||
> 0 \\
|
||||
> 0
|
||||
> \end{matrix}\right)
|
||||
|
||||
1. Vektor $v$ bestimmen
|
||||
$$v = a_1 + sign(a_{11}) \cdot |a_1| \cdot e$$
|
||||
2. Vektor normieren:
|
||||
$$u = \frac{1}{|v|} \cdot v =
|
||||
\frac{1}{\sqrt{1^2 + 2^2 + 3^2}} \cdot
|
||||
\left(\begin{matrix}
|
||||
1 \\
|
||||
2 \\
|
||||
3
|
||||
\end{matrix}\right) =
|
||||
\frac{1}{\sqrt{14}} \cdot
|
||||
\left(\begin{matrix}
|
||||
1 \\
|
||||
2 \\
|
||||
3
|
||||
\end{matrix}\right)$$
|
||||
2. Die Housholder-Matrix $H = I_n - 2 \cdot u \cdot u^T$ berechnen.
|
||||
$$H =
|
||||
\left(\begin{matrix}
|
||||
1 & 0 & 0 \\
|
||||
0 & 1 & 0 \\
|
||||
0 & 0 & 1
|
||||
\end{matrix}\right) -
|
||||
2 \cdot \frac{1}{\sqrt{14}} \cdot
|
||||
\left(\begin{matrix}
|
||||
1 \\
|
||||
2 \\
|
||||
3
|
||||
\end{matrix}\right) \cdot
|
||||
\frac{1}{\sqrt{14}} \cdot
|
||||
\left(\begin{matrix}
|
||||
1 & 2 & 3
|
||||
\end{matrix}\right) \\
|
||||
H =
|
||||
\left(\begin{matrix}
|
||||
1 & 0 & 0 \\
|
||||
0 & 1 & 0 \\
|
||||
0 & 0 & 1
|
||||
\end{matrix}\right) -
|
||||
2 \cdot \frac{1}{14} \cdot
|
||||
\left(\begin{matrix}
|
||||
1 & 2 & 3 \\
|
||||
2 & 4 & 6 \\
|
||||
3 & 6 & 9
|
||||
\end{matrix}\right) =
|
||||
-\frac{1}{7} \cdot
|
||||
\left(\begin{matrix}
|
||||
-6 & 2 & 3 \\
|
||||
2 & -3 & 6 \\
|
||||
3 & 6 & 2
|
||||
\end{matrix}\right)$$
|
||||
|
||||
<div class="letters">
|
||||
|
||||
- $H$: Housholder-Matrix
|
||||
- $I$: Identitäts-Matrix
|
||||
- $n$: Anzahl Dimensionen der Matrix
|
||||
|
||||
</div>
|
||||
|
||||
#### Vorgang
|
||||
Im Rahmen des Vorgangs entspricht $A_1$ der Matrix $A$.
|
||||
|
||||
Die $QR$-Zerlegung kann folgendermassen durchgeführt werden:
|
||||
|
||||
1. $R = A$
|
||||
2. $Q = I_n$
|
||||
3. Für $i$ von $1$ bis $n - 1$
|
||||
1. Gemäss vorheriger Anleitung Householder-Matrix $H_i$ für die erste Spalte von $A_i$ berechnen
|
||||
2. Householder-Matrix um Identitäts-Matrix erweitern. Beispiel:
|
||||

|
||||
3. Erweiterte Householder-Matrix als $Q_i$ speichern
|
||||
4. $R = Q_i \cdot R$
|
||||
5. $Q = Q \cdot Q_i^T$
|
||||
|
||||
***Code-Beispiel:***
|
||||
|
||||
```py
|
||||
from numpy import array, identity, sign, sqrt, square, sum, zeros
|
||||
|
||||
def qrDecomposition(A):
|
||||
A = array(A)
|
||||
n = A.shape[0]
|
||||
R = A.reshape((n, n))
|
||||
Q = identity(n)
|
||||
|
||||
for i in range(n - 1):
|
||||
I = identity(n - i)
|
||||
Qi = identity(n)
|
||||
e = zeros((n - i, 1))
|
||||
e[0][0] = 1
|
||||
a = R[i:,i:i + 1]
|
||||
v = a + sign(a[0]) * sqrt(sum(square(a))) * e
|
||||
u = (1 / sqrt(sum(square(v)))) * v
|
||||
H = I - 2 * u @ u.T
|
||||
Qi[i:,i:] = H
|
||||
R = Qi @ R
|
||||
Q = Q @ Qi.T
|
||||
return [Q, R]
|
||||
```
|
||||
|
||||
## Formelbuchstaben
|
||||
<div class="letters">
|
||||
|
||||
|
|
@ -728,14 +890,18 @@ Wenn die $LR$-Zerlegung, wie in diesem Code, Zeilenaustausch und das Berechnen v
|
|||
- $[a,b]$: Das Untersuchungs-Interval für den Banachschen Fixpunktsatz
|
||||
- $A$: Matrix eines linearen Gleichungssystems
|
||||
- $\tilde{A}$: Umgewandelte Version der Matrix $A$
|
||||
- $A^T$: Transformierte Matrix $A$
|
||||
- $b$: Das gewünschte Resultat eines linearen Gleichungssystems
|
||||
- $B$: Basis der Maschinenzahl
|
||||
- $e$: Exponent der Maschinenzahl
|
||||
- $H$: Housholder-Matrix (siehe $QR$-Zerlegung)
|
||||
- $I$: Identitäts-Matrix (Matrix, überall den Wert $0$ und auf der Diagonalen den Wert $1$ hat)
|
||||
- $K$: Konditionszahl
|
||||
- $L$: Untere Dreiecksmatrix/Normierte Matrix
|
||||
- $m$: Mantisse (Darstellbarer Bereich der Maschinenzahl)
|
||||
- $n$: Anzahl möglicher Stellen der Mantisse $m$
|
||||
- $q$: Konvergenz-Ordnung
|
||||
- $Q$: Orthogonal-Matrix in der $QR$-Zerlegung
|
||||
- $R$: Obere Dreiecksmatrix
|
||||
- $x$: Darzustellender Wert
|
||||
- $x_n$: Die $n$-te Approximation von $x$
|
||||
|
|
|
|||
Loading…
Reference in a new issue