# Höhere Mathematik
## Inhalt
- [Höhere Mathematik](#höhere-mathematik)
- [Inhalt](#inhalt)
- [Einführung](#einführung)
- [Einsatzgebiet](#einsatzgebiet)
- [Arten von Lösungen](#arten-von-lösungen)
- [Verbindung zur Informatik](#verbindung-zur-informatik)
- [Typische Fragestellungen](#typische-fragestellungen)
- [Rechnerarithmetik](#rechnerarithmetik)
- [Maschinenzahl](#maschinenzahl)
- [Grenzen von Maschinenzahlen](#grenzen-von-maschinenzahlen)
- [Datentypen gem. IEEE](#datentypen-gem-ieee)
- [Rundungsfehler und Maschinengenauigkeit](#rundungsfehler-und-maschinengenauigkeit)
- [Konditionszahl](#konditionszahl)
- [Nullstellenprobleme](#nullstellenprobleme)
- [Problemstellung und Ansatz](#problemstellung-und-ansatz)
- [Fixpunktiteration](#fixpunktiteration)
- [Banachscher Fixpunktsatz](#banachscher-fixpunktsatz)
- [Newton-Verfahren](#newton-verfahren)
- [Sekantenverfahren](#sekantenverfahren)
- [Konvergenz-Ordnung](#konvergenz-ordnung)
- [Fehlerabschätzung](#fehlerabschätzung)
- [Formelbuchstaben zu Nullstellenproblem](#formelbuchstaben-zu-nullstellenproblem)
- [Lineare Gleichungssysteme](#lineare-gleichungssysteme)
- [Eigenschaften](#eigenschaften)
- [Dreiecks-Matrizen](#dreiecks-matrizen)
- [Der Gauss-Algorithmus](#der-gauss-algorithmus)
- [Fehlerfortpflanzung und Pivotisierung](#fehlerfortpflanzung-und-pivotisierung)
- [Determinanten-Bestimmung](#determinanten-bestimmung)
- [Die $LR$-Zerlegung](#die-lr-zerlegung)
- [$QR$-Zerlegung](#qr-zerlegung)
- [Housholder-Matrizen](#housholder-matrizen)
- [Vorgang](#vorgang)
- [Fehlerrechnung bei linearen Gleichungssystemen](#fehlerrechnung-bei-linearen-gleichungssystemen)
- [Vektor- und Matrixnormen](#vektor--und-matrixnormen)
- [Aufwand-Abschätzung](#aufwand-abschätzung)
- [Iterative Verfahren zur Lösung von Gleichungssystemen](#iterative-verfahren-zur-lösung-von-gleichungssystemen)
- [$LDR$-Zerlegung](#ldr-zerlegung)
- [Jacobi-Verfahren](#jacobi-verfahren)
- [Gauss-Seidel-Verfahren](#gauss-seidel-verfahren)
- [Konvergenz](#konvergenz)
- [Komplexe Zahlen](#komplexe-zahlen)
- [Rechen-Regeln](#rechen-regeln)
- [Eigenwerte und Eigenvektoren](#eigenwerte-und-eigenvektoren)
- [Numerische Bestimmung von Eigenwerten und Eigenvektoren](#numerische-bestimmung-von-eigenwerten-und-eigenvektoren)
- [Theorie](#theorie)
- [$QR$-Verfahren](#qr-verfahren)
- [Vektor-Iteration](#vektor-iteration)
- [Formelbuchstaben](#formelbuchstaben)
## Einführung
### Einsatzgebiet
- Annähern komplexer Formeln in endlicher Zeit
- Berechnung von Algorithmen durch Computer
- Algorithmen ohne expliziter Lösungsdarstellung
- Alternative Lösungsvorgänge für höhere Performance
### Arten von Lösungen
- Direkte Verfahren - Exakte Lösung nach endlicher Zeit
- Näherungsverfahren/Iteratives Verfahren - Approximation nach begrenzter Anzahl Rechenschritte
### Verbindung zur Informatik
- Effiziente Berechnung numerischer Algorithmen
- Speicherung und Darstellung von Zahlen
- Computergrafik & Bildverarbeitung
- Neuronale Netze
### Typische Fragestellungen
- Wie wirkt sich die Beschränkung der Anzahl Bits für Zahlenformate auf Rechenergebnisse und Rechengenauigkeit aus?
- Numerische Lösung von Nullstellenproblemen
- Numerische Integration
## Rechnerarithmetik
### Maschinenzahl
Maschinenzahlen werden als Zahlen $x$ in folgender Form dargestellt:
$x = m \cdot B^e$
- $x$: Die zu repräsentierende Zahl
- $m$: Die Mantisse (der darstellbare Zahlenwert)
- $B$: Die Basis der zu repräsentierenden Zahl
- $e$: Der Exponent (der Stellenwert der Mantisse $m$)
Beispiel:
$1337 = 0.1337 * 10^4$
Maschinenzahlen sind normalisiert, wenn
- für die Mantisse $m$ $0.1 <= |m| < 1.0$ zutrifft
Maschinenzahlen werden normalisiert, damit es zu jedem Wert eine eindeutige Darstellung als Maschinenzahl gibt.
### Grenzen von Maschinenzahlen
$x_{max} = B^{e_{max}} - B^{e_{max}-n} = (1 - B^{-n}) \cdot B^{e_{max}}$
$x_min = B^{e_{min} - 1}$
### Datentypen gem. IEEE
`float` oder `single`: 32 Bit - 1 Bit für Vorzeichen, 23 Bit für Mantisse $m$, 8 Bit für Exponent $e$
`double`: 64 Bit - 1 Bit für Vorzeichen, 52 für Mantisse $m$, 11 Bit für Exponent $e$
### Rundungsfehler und Maschinengenauigkeit
Absoluter Fehler:
$$|\tilde{x} - x|$$
Relativer Fehler:
$$\frac{|\tilde{x} - x|}{|x|}$$
Maximaler **absoluter** Rundungsfehler:
$$\frac{B}{2} \cdot B^{e - n - 1}$$
**Maschinengenauigkeit** oder maximaler **relativer** Rundungsfehler:
$$\frac{1}{2} \cdot B^{1 - n}$$
Fehlerfortpflanzung bei Funktionsauswertung:
Relativ:
$$\frac{|f'(x)| \cdot |x|}{|f(x)|} \cdot \frac{|\tilde{x} - x|}{|x|}$$
Absolut:
$$|f'(x)| \cdot |\tilde{x} - x|$$
- $B$: Die Basis der Maschinenzahl
- $e$: Der Exponent der Maschinenzahl (Standard-Wert: $0$)
- $n$: Die Anzahl Stellen der Mantisse $m$
- $x$: Der darzustellende Wert
- $\tilde{x}$: Die Annäherung/Approximation an $x$
- $f$: Auszuwertende Funktion
### Konditionszahl
Die Konditionszahl gibt an, wie gross der potenzielle relative Fehler einer numerischen Lösung ist.
Eine niedrige Konditionszahl ($K \le 1$) bedeutet einen niedrigen Fehler, eine hohe Konditionszahl ein grosses Fehlerrisiko.
Formel:
Konditionszahl:
$$K = \frac{|f'(x)| \cdot |x|}{|f(x)|}$$
## Nullstellenprobleme
### Problemstellung und Ansatz
Es wird der korrekte Wert $x$ für eine Aufgabe gesucht.
1. Aufgabe ausformulieren:
$x = \sqrt{A}$
2. Aufgabe zu Nullstellenproblem umformulieren (Funktion, die bei gesuchtem $x$ immer $0$ ergibt):
$f(x) = x^2 - A$
3. (Algorithmisch) richtiges $x$ finden, bei dem die Funktion $0$ ergibt
4. Das gefundene $x$ ist die Lösung
> ***Note:***
> Als Ausgangsbedingung für eine numerische Lösung eines Nullstellenproblems können diverse Bedingungen verwendet werden wie etwa:
> - Eine bestimmte Anzahl Iterationen
> - Abstand zwischen $x_n$ und $x_{n + 1}$ unterschreitet Threshold (approximiertes Resultat)
> - Ein niedriger Threshold ergibt ein genaueres Resultat
> - Ein Threshold von $0$ ergibt das genaue Resultat
### Fixpunktiteration

Ein möglicher Ansatz für ein solches Problem ist eine Fixpunktiteration.
Der Vorgang für eine solche ist folgende:
1. Die Funktion in die Form $F(x) = x$.
Beispiel für $f(x) = x^2 - A$:
$F(x) = \sqrt{A}$
2. Beliebigen Wert für $x_0$ wählen (vorzugsweise Wert in Nähe von erwarteter Lösung)
3. Fixpunktiteration $x_{n + 1}$ berechnen:
$x_{n+1} = F(x_n)$
Dies wird durchgeführt bis die Ausgangsbedingung erfüllt ist.
***Code-Beispiel:***
```py
import math
threshold = 10 ** -6
def f(x): # Funktion f in Nullstellenform
return math.cos(x) - x
def F(x): # Funktion f in Fixpunktform
return math.cos(x)
def F_(x): # Die Ableitung F'(x)
return return -math.sin(x)
x = 0.75 # Startwert - angenommene, etwaige Lösung
if F_(x) >= 1:
print("Fehler: Fixpunktiteration divergiert!")
else:
while math.abs(x - F(x)) >= threshold:
x = F(x)
print(f"Approximierte Lösung: {x}")
```
**Konvergenz**
Eine Fixpunktiteration is konvergent (also berechenbar), wenn folgendes zutrifft:
$$|F'(\tilde{x})| < 1$$
**Divergenz**
Eine Fixpunktiteration is divergent (also unberechenbar), wenn folgendes zutrifft:
$$|F'(\tilde{x})| \ge 1$$
- $F(x)$: Die Fixpunktgleichung
- $F'(x)$: Die Ableitung der Fixpunktgleichung
- $x$: Das genaue Resultat für $x$
- $\tilde{x}$: Das approximierte Resultat für $x$ (Fixpunkt)
- $x_n$: Die $n$-te Approximation für $x$
#### Banachscher Fixpunktsatz
Der Fixpunktsatz dient dazu, abzuschätzen, wie gross der Fehler des Ergebnisses einer Fixpunktiteration in etwa ist.
Fixpunktsatz:
$$|F(x) - F(y)| \le \alpha \cdot |x - y| \text{für alle }x,y \in [a, b]$$
Alternative Umformung:
$$\frac{|F(x) - F(y)|}{|x - y|} \le \alpha$$
**Fehlerabschätzung:**
a-priori Abschätzung:
$$|x_n - \overline{x}| \le \frac{\alpha^n}{1 - \alpha} \cdot |x_1 - x_0|$$
a-posteriori Abschätzung:
$$|x_n - \overline{x}| \le \frac{\alpha}{1 - \alpha} \cdot |x_n - x_{n - 1}|$$
Konstante $\alpha$:
$$\alpha = \max_{x_0 \in [a, b]}| F'(x_0)|$$
$$\alpha \approx |F'(\tilde{x})|$$
Folgendermassen kann dieser aufgestellt werden:
> ***Note:***
> In dieser Passage wird sowohl $a$ (der Buchstabe "a") als auch $\alpha$ (Alpha) verwendet. Diese haben hier eine unterschiedliche Bedeutung.
1. Start- und Endpunkt $a$ und $b$ auswählen, welche genau einen Fixpunkt $\tilde{x}$ beinhalten
2. Prüfen, ob folgendes Zutrifft: Alle Ergebnisse von $F([a, b])$ befinden sich im Intervall $[a, b]$
3. Konstante $\alpha$ berechnen (gem. Formel)
4. Die a-priori und die a-posteriori Abschätzung kann nun beliebig angewendet werden. Hierbei wird für $x_0$ der Wert $a$ verwendet.
### Newton-Verfahren

Das Newton-Verfahren erreicht die Konvergenz (d.h. das (approximierte) Resultat) um einiges schneller.
Hierfür wird die Funktion $f$ in der Nullstellenform benötigt ($f(x) = \text{[...]} = 0$).
Newton-Verfahren:
$$x_{n + 1} = x_n - \frac{f(x_n)}{f'(x_n)}$$
Vereinfachtes Newton-Verfahren:
$$x_{n + 1} = x_n - \frac{f(x_n)}{f'(x_0)}$$
Konvergenz-Kontrolle:
$$\left|\frac{f(x) \cdot f''(x)}{(f'(x))^2}\right| < 1$$
Das Ergebnis ist wahr, wenn mit dem gewählten $x$ eine Konvergenz erreicht werden kann.
1. Startpunkt $x_0$ in der Nähe einer Nullstelle wählen
2. (Wahlweise vereinfachtes) Newton-Verfahren anwenden bis $x_n$ und $x_{n + 1}$ bis Ausgangsbedingung erreicht wird
### Sekantenverfahren

$$x_{n + 1} = x_n - \frac{x_n - x_{n - 1}}{f(x_n) - f(x_{n - 1})} \cdot f(x_n)$$
Vorgang:
1. Startpunkte $x_0$ und $x_1$ wählen (Punkte, die eine Nullstelle umschliessen)
2. Iteration durchführen, bis Ausgangsbedingung erfüllt wird
### Konvergenz-Ordnung
Ein Verfahren hat eine Konvergenz-Ordnung $q \ge 1$, wenn es eine Konstante $c > 0$ für die für alle $n$ Iterations-Schritte gilt:
$$|x_{n + 1} - \overline{x}| \le c \cdot |x_n - x}|^q$$
- $c$: Beliebige Konstante
- $q$: Konvergenz-Ordnung
- Für Newton-Verfahren: $q = 2$
- Für vereinfachtes Newton-Verfahren: $q = 1$
- Für Sekanten-Verfahren: $1 = (1 + \sqrt{5}) : 2 \approx 1.618$
### Fehlerabschätzung
Wenn folgendes zutrifft:
$$f(x_n - \varepsilon) \cdot f(x_n + \varepsilon) < 0$$
Schneidet $f$ zwischen $x_n - \varepsilon$ und $x_n + \varepsilon$ die Nullstelle.
Deswegen gilt folgendes:
$$|x_n - \xi| < \varepsilon$$
Sprich: Der Fehler ist kleiner als $\varepsilon$.
Vorgang:
- $\varepsilon$ suchen, für die oben genannte Bedingung zutrifft
- Der maximale Fehler ist $\varepsilon$
- $x_n$: Der approximierte $x$-Wert nach der $n$-ten Iteration
- $\varepsilon$: Der maximale Fehler
- $\xi$: Der Schnittpunkt der Nullstelle
### Formelbuchstaben zu Nullstellenproblem
- $\alpha$: Lipschitz-Konstante
- $[a, b]$: Der
- $F(x)$: Die Fixpunktgleichung
- $F'(x)$: Die Ableitung der Fixpunktgleichung
- $x$ und $y$: Beliebig gewählte Punkte im Interval $[a,b]$
- $\tilde{x}$: Das approximierte Resultat für $x$ (Fixpunkt)
- $x_n$ Die $n$-te Approximation von $x$
## Lineare Gleichungssysteme
**Lineares Gleichungssystem:**
Lineare Gleichungssysteme haben jeweils die Form $A \cdot x = b$ wobei $A$ und $b$ gegeben und $x$ gesucht ist:
$$A = \left(
\begin{matrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{matrix}
\right),
x = \left(
\begin{matrix}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{matrix}
\right),
b = \left(
\begin{matrix}
b_1 \\
b_2 \\
\vdots \\
b_n
\end{matrix}
\right)$$
### Eigenschaften
- Gleich viele gesuchte Variablen $x_n$ wie Gleichungen $n$. Folglich:
- Die Matrix $A$ ist eine quadratische Matrix mit Dimensionen $n \times n$
- $A$ ist invertierbar
- $A$ hat eine Determinante $\det(A)$
### Dreiecks-Matrizen
***$L$: Untere Dreiecksmatrix***
Eine Matrix, die in der oberen rechten Ecke nur den Wert $0$ und auf der Diagonale nur den Wert $1$ hat. Eine Untere Dreiecksmatrix hat also folgende Form:
$$L = \left(
\begin{matrix}
1 & 0 & 0 & \cdots & 0 \\
l_{21} & 1 & 0 & \cdots & 0 \\
l_{31} & l_{32} & 1 & \ddots & 0 \\
\vdots & \vdots & \ddots & \ddots & 0 \\
l_{n1} & l_{n2} & \cdots & l_{nn - 1} & 1
\end{matrix}
\right)$$
***$R$: Obere Dreiecksmatrix***
Eine Matrix, die unten links von der Diagonale nur den Wert $0$ beinhaltet. Eine Obere Dreiecksmatrix hat dementsprechend folgende Form:
$$R = \left(
\begin{matrix}
r_{11} & r_{12} & r_{13} & \cdots & r_{1n} \\
0 & r_{22} & r_{23} & \cdots & r_{2n} \\
0 & 0 & r_{33} & \cdots & r_{3n} \\
\vdots & \vdots & \ddots & \ddots & \vdots \\
0 & 0 & \cdots & 0 & r_{nn}
\end{matrix}
\right)$$
***Code-Beispiele:***
_Umwandlung in $R$-Matrix:_
```py
for i in range(n):
if A[i, i] == 0:
index = -1
for j in range(i + 1, n):
if A[j, i] > 0:
index = j
if index == -1:
raise Exception("Invalid Matrix")
else:
# Swap lines
A[[i, index]] = A[[index, i]]
for j in range(i + 1, n):
factor = A[j, i] / A[i, i]
A[j] = A[j] - (factor * A[i])
```
### Der Gauss-Algorithmus
Der Gauss-Algorithmus basiert darauf, dass ein lineares Gleichungssystem leicht lösbar ist, falls $A$ eine obere Dreiecksmatrix ist. $A$ muss also hierfür die Form einer oberen Dreiecksmatrix $R$ haben.
***Gauss-Algorithmus:***
$$x_i = \frac{b_i - \sum_{j = i + 1}^n{a_{ij} \cdot x_j}}{a_{ii}}, i = n, n - 1, \dots, 1$$
Um den Gauss-Algorithmus anzuwenden, muss die Matrix $A$ erst in eine $R$-Matrix umgewandelt werden. Dies funktioniert wie folgt:
1. Mit $i$ von $1$ bis $n$
2. Falls $a_{ii}$ den Wert $0$ hat:
1. Mit $j$ von $i + 1$ bis $n$
2. Prüfen, ob $a_{ji}$ einen höheren Wert als $0$ hat
- Falls Zeile gefunden wurde:
- $a_{i}$ mit $a_{j}$ tauschen
- $b_{i}$ mit $b_{j}$ tauschen
- Sonst beenden: ungültige Matrix
3. Mit $j$ von $i + 1$ bis $n$
1. $a_k = a_k - \frac{a_{ki}}{a_{ii}} \cdot a_i$
2. $b_k = b_k - \frac{a_{ki}}{a_{ii}} \cdot b_i$
***Code-Beispiel:***
```py
from numpy import array, zeros
def gaussMethod(A, b):
A = array(A)
n = A.shape[0]
A = A.reshape((n, n))
b = array(b).reshape((n))
result = zeros(n)
# Convert to R-Matrix
for i in range(n):
maxIndex = i
for j in range(i + 1, n):
if A[j, i] > A[maxIndex, i]:
maxIndex = j
# Swap lines
A[[i, maxIndex]] = A[[maxIndex, i]]
b[[i, maxIndex]] = b[[maxIndex, i]]
for j in range(i + 1, n):
factor = A[j, i] / A[i, i]
A[j] = A[j] - (factor * A[i])
b[j] = b[j] - (factor * b[i])
# Calculate result
for index in range(n, 0, -1):
i = index - 1
value = b[i]
for j in range(i, n):
value = value - A[i, j] * result[j]
result[i] = value / A[i, i]
return result.reshape((n, 1))
```
### Fehlerfortpflanzung und Pivotisierung
- Da beim Umwandeln einer Matrix $A$ in die $R$-Form Zeilen in jedem Schritt mit dem Faktor $\lambda = \frac{a_{ji}}{a_{ii}}$ multipliziert werden, vergrössert sich der Schritt immer um $|\lambda|$
- $\lambda$ kann klein gehalten werden, indem Zeilen der Grösse nach sortiert werden
- In den Code-Beispielen ist dies bereits berücksichtigt
### Determinanten-Bestimmung
Die Determinante einer Matrix $A$ lässt sich einfach berechnen, sobald sie in die $R$-Form gebracht wurde mit folgender Formel:
Determinanten-Bestimmung mit Matrix $\tilde{A}$ (die Matrix $A$ in der $R$-Form):
$$\det(A) =
(-1)^l \cdot \det(\tilde{A}) =
(-1)^l \cdot \prod_{i = 1}^n{\tilde{a_{ii}}}$$
***Code-Beispiel:***
```py
from numpy import array
def det(A):
l = 0
n = A.shape[0]
A = A.reshape((n, n))
# Convert to R-Matrix
for i in range(n):
maxIndex = i
for j in range(i + 1, n):
if A[j, i] > A[maxIndex, i]:
maxIndex = j
# Swap lines
A[[i, maxIndex]] = A[[maxIndex, i]]
l = l + 1
for j in range(i + 1, n):
factor = A[j, i] / A[i, i]
A[j] = A[j] - (factor * A[i])
result = 1
for i in range(n):
result = result * A[i, i]
return (-1 ** l) * result
```
### Die $LR$-Zerlegung
In der $LR$-Zerlegung wird die Matrix $A$ in die Matrizen $L$ und $R$ aufgeteilt, sodass $A = L \cdot R$ gilt.
Alternative Namen dieses Vorgangs sind ***$LR$-Faktorisierung*** und $LU$-decomposition.
Für in $L$ und $R$ zerlegte Matrizen gilt:
$$A \cdot x = b$$
und
$$A \cdot x = L \cdot R \cdot x = L \cdot y = b$$
Aufwand: Berechnung der $LR$-Zerlegung mit Gauss-Algorithmus benötigt ca. $\frac{2}{3}n^3$ Punktoperationen.
Falls Zeilenvertauschungen stattfinden, entsteht bei der $LR$-Zerlegung eine zusätzliche Permutations-Matrix $P$.
Für $L$ und $R$ zerlegte Matrizen mit Permutation $P$ gilt:
$$P \cdot A = L \cdot R$$
$$L \cdot y = P \cdot b$$
$$R \cdot x = y$$
Das Verfahren für die $LR$-Zerlegung ist identisch zu den Schritten bei der Umwandlung in eine $R$-Matrix. Jedoch wird jeweils der Wert $l_{ji}$ in der (zu Beginn) leeren Matrix $L$ mit dem im aktuellen Eliminationsschritt gesetzt. Zudem muss bei Vertauschungen die Permutations-Matrix $P$ entsprechend angepasst werden:
***Code-Beispiel:***
```py
from numpy import array, identity, zeros
def decomposite(A):
l = 0
n = A.shape[0]
R = A.reshape((n, n))
L = zeros((n, n))
P = identity((n, n))
# Convert to LR-Matrix
for i in range(n):
maxIndex = i
for j in range(i + 1, n):
if A[j, i] > A[maxIndex, i]:
maxIndex = j
# Swap lines
Pn = identity((n, n))
A[[i, maxIndex]] = A[[maxIndex, i]]
Pn[[i, maxIndex]] = Pn[[maxIndex, i]]
P = P * Pn
for j in range(i + 1, n):
factor = R[j, i] / R[i, i]
L[j, i] = factor
R[j] = R[j] - (factor * R[i])
result = 1
for i in range(n):
result = result * R[i, i]
return [L, R, P]
```
Wenn die $LR$-Zerlegung, wie in diesem Code, Zeilenaustausch und das Berechnen von $P$ involviert, spricht man von einer $LR$-Zerlegung mit **Spaltenmaximum-Strategie**.
***Vorgang:***
1. Gemäss vorhergehender Beschreibung und Code-Beispiel die Matrizen $L$ und $R$ berechnen
2. Mit Hilfe des Gauss-Algorithmus $L \cdot y = P \cdot b$ nach $y$ auflösen
3. Mit Hilfe des Gauss-Algorithmus $R \cdot x = y$ nach $x$ auflösen
### $QR$-Zerlegung
- Die Matrix $A$ wird in eine orthogonale Matrix $Q$ und eine obere Dreiecksmatrix $R$ zerlegt.
- Orthogonal-Matrizen beschreiben Drehungen, Spiegelungen oder Kombinationen daraus.
- Eine $QR$-Zerlegung erfordert ca. $\frac{5}{3}n^3$ Punktoperationen - ca. doppelt so viel wie die $LR$-Zerlegung.
***Orthogonal-Matrix:***
Eine Matrix $Q$ ist orthogonal, wenn folgendes gilt:
$$Q^T \cdot Q = I_n$$
($x^T$ steht hierbei für eine **T**ransformation)
#### Housholder-Matrizen
Im Rahmen der Berechnung der Matrizen $Q$ und $R$ werden sogenannte "Housholder-Matrizen" berechnet.
***Housholder-Matrizen:***
Sei $u$ ein Vektor mit beliebig vielen Dimensionen, für den gilt:
$$|u| = \sqrt{u_1^2 + u_2^2 + \dots + u_n^2} = 1$$
Die Householder-Matrix hat folgende Eigenschaft:
$$H := I_n - 2 \cdot u \cdot u^T$$
Für Housholder-Matrizen gilt zudem folgendes:
$$H = H^T = H^{-1}$$
und
$$H \cdot H = I_n$$
***Berechnung einer Housholder-Matrix***
Beispiel der Berechnung einer Housholder-Matrix zur ersten Spalte der Matrix $A$.
> Für die Berechnung wird ein Einheitsvektor $e$ benötigt, welcher genauso viele Werte hat, wie die Matrix Dimensionen. Ein Einheitsvektor hat im ersten Feld den Wert $1$ und in allen anderen Feldern der Wert $0$.
>
> Für eine Matrix $A$ mit der Dimension $n = 3$ lautet der Einheitsvektor $e$ also wie folgt:
> $$e = \left(\begin{matrix}
> 1 \\
> 0 \\
> 0
> \end{matrix}\right)
1. Vektor $v$ bestimmen
$$v = a_1 + sign(a_{11}) \cdot |a_1| \cdot e$$
2. Vektor normieren:
$$u = \frac{1}{|v|} \cdot v =
\frac{1}{\sqrt{1^2 + 2^2 + 3^2}} \cdot
\left(\begin{matrix}
1 \\
2 \\
3
\end{matrix}\right) =
\frac{1}{\sqrt{14}} \cdot
\left(\begin{matrix}
1 \\
2 \\
3
\end{matrix}\right)$$
2. Die Housholder-Matrix $H = I_n - 2 \cdot u \cdot u^T$ berechnen.
$$H =
\left(\begin{matrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{matrix}\right) -
2 \cdot \frac{1}{\sqrt{14}} \cdot
\left(\begin{matrix}
1 \\
2 \\
3
\end{matrix}\right) \cdot
\frac{1}{\sqrt{14}} \cdot
\left(\begin{matrix}
1 & 2 & 3
\end{matrix}\right) \\
H =
\left(\begin{matrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{matrix}\right) -
2 \cdot \frac{1}{14} \cdot
\left(\begin{matrix}
1 & 2 & 3 \\
2 & 4 & 6 \\
3 & 6 & 9
\end{matrix}\right) =
-\frac{1}{7} \cdot
\left(\begin{matrix}
-6 & 2 & 3 \\
2 & -3 & 6 \\
3 & 6 & 2
\end{matrix}\right)$$
- $H$: Housholder-Matrix
- $I$: Identitäts-Matrix
- $n$: Anzahl Dimensionen der Matrix
#### Vorgang
Im Rahmen des Vorgangs entspricht $A_1$ der Matrix $A$.
Die $QR$-Zerlegung kann folgendermassen durchgeführt werden:
1. $R = A$
2. $Q = I_n$
3. Für $i$ von $1$ bis $n - 1$
1. Gemäss vorheriger Anleitung Householder-Matrix $H_i$ für den Vektor `A[i:,i:i + 1]` berechnen (`i`-te Spalte ab Zeile `i`)
2. Householder-Matrix um Identitäts-Matrix erweitern. Beispiel:
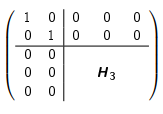
3. Erweiterte Householder-Matrix als $Q_i$ speichern
4. $R = Q_i \cdot R$
5. $Q = Q \cdot Q_i^T$
6. Die Gleichung $R \cdot x = Q^T \cdot b$ mit Gauss-Algorithmus lösen
***Code-Beispiel:***
```py
from numpy import array, identity, sign, sqrt, square, sum, zeros
def qrSolve(A, b):
A = array(A)
n = A.shape[0]
R = A.reshape((n, n))
Q = identity(n)
for i in range(n - 1):
I = identity(n - i)
Qi = identity(n)
e = zeros((n - i, 1))
e[0][0] = 1
a = R[i:,i:i + 1]
v = a + sign(a[0]) * sqrt(sum(square(a))) * e
u = (1 / sqrt(sum(square(v)))) * v
H = I - 2 * u @ u.T
Qi[i:,i:] = H
R = Qi @ R
Q = Q @ Qi.T
R[i + 1:,i:i + 1] = zeros((n - (i + 1), 1))
return linalg.solve(R, Q.T @ b)
```
### Fehlerrechnung bei linearen Gleichungssystemen
Ähnlich wie herkömmliche Gleichungen, können Gleichungssysteme nicht mit eindeutiger Genauigkeit berechnet werden. Es entsteht ein Fehler.
***Fehler bei linearen Gleichungssystemen:***
$$A \cdot \tilde{x} = \tilde{b} = b + \Delta b$$
$$\Delta x = \tilde{x} - x$$
- $A$: Matrix eines linearen Gleichungssystems
- $b$: Gewünschtes Ergebnis des Gleichungssystems
- $\tilde{b}$: Ergebnis des Gleichungssystems unter Verwendung von $\tilde{x}$ in $A \cdot \tilde{x}$
- $\Delta b$: Residuum: Die Differenz von $b$ und $\tilde{b}$
- $x$: Genaue Lösung
- $\tilde{x}$: Näherungslösung von $x$
- $\Delta x$: Der Fehler der Näherungslösung $\tilde{x}$
#### Vektor- und Matrixnormen
***Vektornormen:***
$1$-Norm, Summen-Norm:
$$||x||_1 = \sum_{i = 1}^n|x_i|$$
$2$-Norm, euklidische Norm:
$$||x||_2 = \sqrt{\sum_{i = 1}^n x_i^2}$$
$\infin$-Norm, Maximum-Norm:
$$||x||_\infin = \max_{i = 1, \dots, n}|x_i|$$
***Matrixnormen:***
$1$-Norm, Spaltensummen-Norm:
$$||A||_1 = \max_{j=1, \dots, n}\sum_{i = 1}^n|a_{ij}|$$
$2$-Norm, Spektral-Norm:
$$||A||_2 = \sqrt{\rho(A^T \cdot A)}$$
$\infin$-Norm, Zeilensummen-Norm:
$$||A||_\infin = \max_{i = 1, \dots, n}\sum_{j = 1}^n|a_{ij}|$$
Folgendes gilt für die Abschätzung von Vektoren und Matrizen:
***Fehlerabschätzung von Vektoren und Matrizen:***
Für die Gleichung $A \cdot x = b$ und die dazugehörige Approximation $A \cdot \tilde{x} = \tilde{b}$ gilt:
Absoluter Fehler:
$$||x - \tilde{x}|| \le ||A^{-1}|| \cdot ||b - \tilde{b}||$$
Falls $||b|| \not = 0$ gilt zudem:
Relativer Fehler:
$$\frac{||x - \tilde{x}||}{||x||} \le ||A|| \cdot ||A^{-1}|| \cdot \frac{||b - \tilde{b}||}{||b||}$$
***Konditionszahl:***
Die Konditionszahl $cond(A)$ einer Matrix $A$ berechnet sich wie folgt:
$$cond(A) = ||A|| \cdot ||A^{-1}||$$
Eine hohe Konditionszahl $cond(A)$ bedeutet, dass kleine Fehler im Vektor $b$ zu grossen Fehlern im Ergebnis $x$ führen können. In diesem Fall ist eine Matrix schlecht konditioniert.
***Fehlerabschätzung von Matrizen mit Fehlern:***
Sollte auch die Matrix $A$ fehlerhaft sein (fehlerhafte Matrix $\tilde{A}$), gilt der nachstehende Satz unter folgender Bedingung:
$$cond(A) \cdot \frac{||A - \tilde{A}||}{||A||} < 1$$
dann gilt:
Relativer Fehler:
$$\frac{||x - \tilde{x}||}{||x||} \le
\frac{cond(A)}{1 - cond(A) \cdot \frac{||A - \tilde{A}||}{||A||}} \cdot
\left(
\frac{||A - \tilde{A}||}{||A||} +
\frac{||b - \tilde{b}||}{||b||}
\right)$$
### Aufwand-Abschätzung
***Kennzahlen:***
Lösung Linearer Gleichungssysteme mit Hilfe von...
Gauss-Elimination:
$$\frac{2}{3}n^3 + \frac{5}{2}n^2 - \frac{13}{6}n$$
$LR$-Zerlegung:
$$\frac{2}{3}n^3 + \frac{7}{2}n^2 + \frac{13}{6}n$$
$QR$-Zerlegung:
$$\frac{5}{3}n^3 + 4n^2 + \frac{7}{3}n - 7$$
***Ordnung $O(n)$***
Die Ordnung $O(n)$ der zuvor genannten Verfahren entspricht der höchsten Potenz von $n$, welche in der Formel zur Berechnung des Aufwands vorkommt.
Das bedeutet also folgendes:
Ordnung von Gauss-Elimination, $LR$-Zerlegung und $QR$-Zerlegung:
$$O(n^3)$$
## Iterative Verfahren zur Lösung von Gleichungssystemen
### $LDR$-Zerlegung
Für die $LDR$-Zerlegung wird die Matrix $A$ in drei Matrizen $L$, $D$ und $R$ aufgeteilt, wobei $L$ eine untere Dreiecksmatrix, $D$ eine Diagonalmatrix und $R$ eine obere Dreiecksmatrix ist. Das bedeutet:
$$A = L + D + R$$
Mit
$$L = \left(
\begin{matrix}
0 & 0 & 0 & \cdots & 0 \\
a_{21} & 0 & 0 & \cdots & 0 \\
a_{31} & a_{32} & 0 & \cdots & 0 \\
\vdots & \vdots & \ddots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn - 1} & 0
\end{matrix}
\right)$$
$$D = \left(
\begin{matrix}
a_{11} & 0 & 0 & \cdots & 0 \\
0 & a_{22} & 0 & \cdots & 0 \\
0 & 0 & a_{33} & \cdots & 0 \\
\vdots & \vdots & \ddots & \ddots & \vdots \\
0 & 0 & \cdots & 0 & a_{nn}
\end{matrix}
\right)$$
$$R = \left(
\begin{matrix}
0 & a_{12} & a_{13} & \cdots & a_{1n} \\
0 & 0 & a_{23} & \cdots & a_{2n} \\
0 & 0 & 0 & \ddots & \vdots \\
\vdots & \vdots & \ddots & \ddots & a_{n-1,n} \\
0 & 0 & \cdots & 0 & 0
\end{matrix}
\right)$$
> ***Wichtig:***
> Hierbei handelt es sich nicht um $L$ und $R$ aus der $LR$-Zerlegung!
### Jacobi-Verfahren
Das Jacobi-Verfahren ist ein iteratives Verfahren, welches nach jeder Iteration näher mit der tatsächlichen Lösung $x$ konvergiert.
Das Jacobi-Verfahren ist auch bekannt als **Gesamtschrittverfahren**.
***Jacobi-Verfahren:***
Zunächst beginnt man mit $x^{(0)}$ als ein Vektor, der nur aus $0$en besteht.
$$x^{(k + 1)} = -D^{-1} \cdot (L + R) \cdot x^{(k)} + D^{-1} \cdot b$$
Für die Berechnung einzelner Elemente des Vektors $x^{(k + 1)}$ gilt:
Für $i$ von $1$ bis $n$:
$$x^{(k + 1)}_i = \frac{1}{a_{ii}} \cdot
\left(
b_i - \sum_{j = 1,j \not = i}^n a_{ij} \cdot x^{(k)}_j
\right)$$
- $x^{(k)}$: Die Annäherung an $x$ nach der $k$-ten Iteration
### Gauss-Seidel-Verfahren
Das Gauss-Seidel-Verfahren konvergiert schneller als das Jacobi-Verfahren.
Da für die Berechnung des Jacobi-Verfahrens für die Berechnung von $x_2$ auch Werte von $x_1$ verwendet werden, können die Werte direkt aus der aktuellen Iteration $k$ wiederverwendet werden, um den Vorgang schneller konvergieren zu lassen.
Das Gauss-Seidel-Verfahren wird auch **Einzelschrittverfahren** genannt.
***Gauss-Seidel-Verfahren:***
$$x^{(k+1)} = -(D + L)^{-1} \cdot R \cdot x^{(k)} + (D + L)^{-1} \cdot b$$
Für die Berechnung einzelner Vektor-Komponente wiederum:
Für $i$ von $1$ bis $n$:
$$x^{(k + 1)}_i = \frac{1}{a_{ii}} \cdot
\left(
b_i - \sum_{j = 1}^{i - 1} a_{ij} \cdot x^{k + 1}_j -
\sum_{j = i + 1}^n a_{ij} \cdot x^{(k)}_j
\right)$$
### Konvergenz
***Anziehung/Abstossung:***
Gegeben sei eine Fixpunkt-Iteration:
$$x^{(n + 1)} = B \cdot x^{(n)} + c =: F(x^{(n)})$$
Beispiele für solche Fixpunkt-Iterationen sind das Jacobi- oder das Gauss-Seidel-Verfahren.
Falls folgendes gegeben ist: $\tilde{x} = B \cdot \tilde{x} + c = F(\tilde{x})$, dann gilt:
- $\tilde{x}$ ist ein anziehender Fixpunkt, falls $||B|| < 1$
- $\tilde{x}$ ist ein abstossender Fixpunkt, falls $||B|| > 1$
***Abschätzungen:***
Gegeben sei eine Fixpunkt-Iteration:
$$x^{(n + 1)} = B \cdot x^{(n)} + c =: F(x^{(n)})$$
Für Fixpunkt-Iterationen bei denen $x^{(k)}$ gegen $\tilde{x}$ konvergiert (gemäss oben stehender Formel "Anziehung/Abstossung"), gelten folgende Abschätzungen:
a-priori Abschätzung:
$$||x^{(n)} - \overline{x}|| \le
\frac{||B||^n}{1 - ||B||} \cdot
||x^{(1)} - x^{(0)}||$$
a-posteriori Abschätzung:
$$||x^{(n)} - \overline{x}|| \le
\frac{||B||}{1 - ||B||} \cdot
||x^{(n)} - x^{(n - 1)}||$$
Die Matrix $B$ hat hierbei je nach verwendetem Verfahren einen anderen Wert:
***Matrix $B$ für Abschätzung und Konvergenz***
- Für das Jacobi-Verfahren:
$$B = -D^{-1} \cdot (L + R)$$
- Für das Gauss-Seidel-Verfahren
$$B = -(D + L)^{-1} \cdot R$$
***Diagonal-Dominanz:***
Die Matrix $A$ ist diagonal-dominant, falls eines der folgenden Kriterien zutrifft:
- Zeilensummen-Kriterium:
- Für alle $i = 1, \dots, n$ gilt:
$$|a_{ii}| > \sum_{j = 1, i \not = j}^n{|a_{ij}|}$$
- Spaltensummen-Kriterium:
- Für alle $i = 1, \dots, n$ gilt:
$$|a_{jj}| > \sum_{i = 1, i \not = j}{|a_{ij}|}$$
Für alle Matrizen, die diagonal-dominant sind gilt, dass sie für das Jacobi- und das Gauss-Seidel-Verfahren konvergieren.
## Komplexe Zahlen
Der Bereich der Komplexen Zahlen dient dazu, Werte abzubilden, die es eigentlich nicht geben kann.
Beispiel einer komplexen Zahl:
$$x^2 = -1$$
Es gibt keinen Wert, der $-1$ ergibt, wenn er quadriert wird. Es handelt sich also um eine komplexe Zahl.
Dafür wird die imaginäre Einheit $i$ eingeführt mit folgender Eigenschaft:
$$i^2 = -1$$
Für diese Definition wäre das Resultat von $x^2= -1$ also $x = \plusmn{i}$
In Python und in der Elektrotechnik wird der Buchstabe $j$ verwendet.
Komplexe Zahlen $z$ mit $z = x + i \cdot y$ können nicht auf einem Zahlenstrahl dargestellt werden.
Sie können in einem Koordinaten-System eingezeichnet werden, wobei $x$ der reale und $y$ der imaginäre Anteil sind:
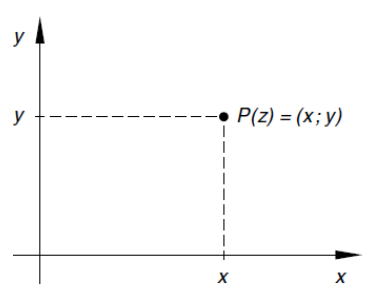
Dieses Koordinaten-System nennt sich auch **Gaussche Zahlenebene**.
***Komplexe Zahlen:***
Imaginäre Einheit $i$:
$$i^2 = -1$$
Komplexe Zahlen $z$:
$$z = x + i \cdot y$$
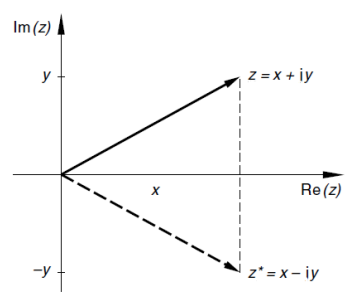
**Konjugierte** komplexe Zahl:
$$z^* = x - i \cdot y$$
Betrag von $z$:
$$|z| = \sqrt{x^2 + y^2}$$
Menge aller komplexen Zahlen $\mathbb{C}$:
$$\mathbb{C} = \{ z | z = x + i \cdot y \text{ mit } x, y \in \mathbb{R}\}$$
Veranschaulichung einer konjugierten komplexen Zahl $z^*$:
- $\mathbb{C}$: Menge aller komplexen Zahlen
- $x$: Realteil einer komplexen Zahl
- $y$: Imaginärteil einer komplexen Zahl
- $z$: Komplexe Zahl
***Darstellungsformen:***
Es gibt diverse Darstellungsformen für komplexe Zahlen:
- Normalform (auch "algebraische" oder "kartesische" Form):
$$z = x + i \cdot y$$
- Trigonometrische Form:
$$z = r \cdot (\cos(\varphi) + i \cdot \sin(\varphi))$$
- Exponential-Form:
$$z = re^{i \cdot \varphi}$$
Beispiel einer komplexen Zahl $z$ in der Normalform und der Trigonometrischen Form:

- $r$: Die Länge des Vektors einer komplexen Zahl $z$ ($r = |z|$)
- $\varphi$: Der Winkel zwischen der x-Achse und dem Vektor der komplexen Zahl $z$
### Rechen-Regeln
***Rechen-Regeln für komplexe Zahlen:***
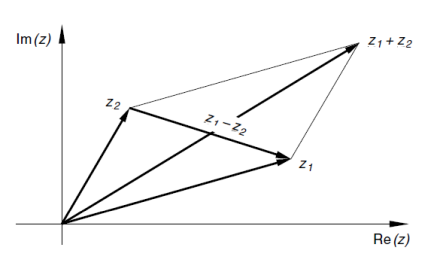
Addition:
$$z_1 + z_2 = (x_1 + x_2) + i \cdot (y_1 + y_2)$$
Subtraktion:
$$z_1 - z_2 = (x_1 - x_2) + i \cdot (y_1 - y_2)$$
Multiplikation:
$$z_1 \cdot z_2 = (x_1 \cdot x_2 - y_1 \cdot y_2) +
i \cdot(x_1 \cdot y_2 + x_2 \cdot y_2)$$
Division:
$$\begin{aligned}
\frac{z_1}{z_2} &=
\frac{z_1 \cdot z_2^*}{z_2 \cdot z_2^*} =
\frac{(x_1 + i \cdot y_1) \cdot (x_2 - i \cdot y_2)}{(x_2 + i \cdot y_2) \cdot (x_2 - i \cdot y_2)} \\
&= \frac{(x_1 \cdot x_2 + y_1 \cdot y_2) + i \cdot (y_1 \cdot x_2 - x_1 \cdot y_2)}{x_2^2 + y_2^2} \\
&= \frac{(x_1 \cdot x_2 + y_1 \cdot y_2)}{x_2^2 + y_2^2} + i \cdot \frac{(y_1 \cdot x_2 - x_1 \cdot y_2)}{x_2^2 + y_2^2}
\end{aligned}$$
Visualisierung von Addition und Subtraktion zwei komplexer Zahlen $z_1$ und $z_2$:
***Potenzieren in der Polarform:***
Für komplexe Zahlen in der Normalform gilt folgendes:
- Sei $n \in \mathbb{N}$:
$$z^n = (r \cdot e^{i \cdot \varphi})^n = r^n \cdot e^{i \cdot n \cdot \varphi} =
r^n \cdot (\cos(n \cdot \varphi) + i \cdot \sin(n \cdot \varphi))$$
***Fundamentalsatz der Algebra:***
Eine algebraische Gleichung $n$-ten Grades mit komplexen Koeffizienten und Variablen $a_i, z \in \mathbb{C}$
$$a_n \cdot z^n + a_{n - 1} \cdot z^{n - 1} + \dots + a_1 \cdot z + a_0 = 0$$
besitzt in der Menge $\mathbb{C}$ der komplexen Zahlen genau $n$ Lösungen.
***Ziehen der Wurzel einer komplexen Zahl:***
Die Gleichung für das Ziehen einer Wurzel $n$ der komplexen Zahl $a$ lautet: $z^n = a$.
Für die Lösung dieser Gleichung existieren genau $n$ verschiedene Lösungen in der Menge $\mathbb{C}$:
$$z_k = r \cdot (\cos(\varphi_k + i \cdot \sin(\varphi_k)) = r \dot e^{i \cdot \varphi_k}$$
für $k = 0, 1, 2, \dots, n - 1$:
mit
$$r = \sqrt[n]{r_0}$$
$$\varphi_k = \frac{\varphi + k \cdot 2 \cdot \pi}{n}$$
Die Bildpunkte der Ergebnisse liegen in der komplexen Zahlenebene auf einem Kreis um den Nullpunkt mit dem Radius $r = \sqrt[n]{r_0}$ und bilden die Ecken eines regelmässigen $n$-Ecks.
Visualisierung des Ziehens der $6$-ten Wurzel einer komplexen Zahl $z$:

## Eigenwerte und Eigenvektoren
Für Matrizen $A$ gibt es Vektoren $x$ und Faktoren $\lambda$, für die gilt:
$$A \cdot x = \lambda \cdot x$$
- $x$-Werte, für die das zutrifft, nennen sich **Eigenvektoren** von $A$
- $\lambda$-Werte, für die das zutrifft, nennen sich **Eigenwerte** von $A$
***Eigenwerte und Eigenvektoren:***
Falls für eine gegebene Matrix $A$, einen beliebigen Vektor $x \not = 0$ und einen beliebigen Wert $\lambda$ folgendes zutrifft:
$$A \cdot x = \lambda \cdot x$$
- $x$ ist ein **Eigenvektor** von $A$
- $\lambda$ ist ein **Eigenwert** von $A$
In manchen Fällen müssen für die Berechnung von Eigenwerten und Eigenvektoren komplexe Vektoren $z$ normiert werden.
Dies funktioniert folgendermassen:
***Normierung komplexer Vektoren:***
$$x = z \cdot \frac{1}{|z|} =
\left(
\begin{matrix}
z_1 \\
\vdots \\
z_n
\end{matrix}
\right) \cdot
\frac{1}{\sqrt{z_1 \cdot z_1^* + \dots + z_n \cdot z_n^*}}$$
- $z$: Komplexer Vektor
- $z_n$: $n$-te Komponente des Vektors $z$
- $x$: Normierter Vektor $z$
***Eigenschaften von Eigenwerten:***
$\lambda$ ist ein Eigenwert von $A$, fals folgendes gilt:
$$det(A - \lambda \cdot I_n) = 0$$
***Eigenwerten und die Spur & Determinante von Matrizen:***
- Die Determinante einer Matrix $A$ ist das Produkt aller Eigenwerte.
- Die Spur (trace) - also die Summe aller Diagonalelemente - ist die Summe aller Eigenwerte
$$det(A) = \lambda_1 \cdot \lambda_2 \dots \lambda_n$$
$$trace(A) = a_{11} + a_{22} + \dots + a_{nn} = \lambda_1 + \lambda_2 + \dots + \lambda_n$$
- Wenn $\lambda$ ein Eigenwert von $A$ ist, so ist der Kehrwert $\frac{1}{\lambda}$ ein Eigenwert der inversen Matrix $A^{-1}$
- Die Vielfachheit, mit der $\lambda$ in der Determinante auftritt nennt sich **algebraische Vielfachheit** von $\lambda$
- Das **Spektrum** $\sigma(A)$ ist die Menge aller Eigenwerte von $A$
***Eigenwerte in speziellen Matrizen:***
Für Diagonal-Matrizen und Dreiecks-Matrizen gilt:
- Die Eigenwerte entsprechen den Diagonal-Elementen.
***Eigenraum:***
Als Eigenraum bezeichnet man eine beliebige Anzahl Vektoren, die alle für dein Eigenwert $\lambda$ gelten.
Indem man diese Vektoren kombiniert, lassen sich beliebig viele neue Eigenvektoren zum Eigenwert $\lambda$ bestimmen.
Für den Eigenwert $\lambda$ von $A$ bilden Eigenvektoren zum Eigenwert $\lambda$ und der Nullvektor $0$ einen **Eigenraum** der Form $\mathbb{C}^n$
- Die Dimension des Eigenraumes von $\lambda$ bestimmt sich durch folgende Formel:
$$n - Rg(A - \lambda \cdot I_n)$$
Das Ergebnis nennt sich **geometrische Vielfachheit** und entspricht der Anzahl unabhängiger Eigenvektoren zum Eigenwert $\lambda$.
- Die geometrische Vielfachheit ist kleiner oder gleich der **algebraischen Vielfachheit**
- $A$: Eine beliebige Matrix
- $x$: Eigenvektor einer Matrix $A$
- $\lambda$: Eigenwert einer Matrix $A$
### Numerische Bestimmung von Eigenwerten und Eigenvektoren
#### Theorie
***Ähnliche Matrizen:***
Eine Matrix $B$ ist zu einer Matrix $A$ ähnlich, wenn für eine beliebige Matrix $T$ gilt:
$$B = T^{-1} \cdot A \cdot T$$
***Diagonalisierbarkeit:***
Eine Matrix $A$ ist _diagonalisierbar_, wenn für eine Matrix $T$ das Ergebnis $D$ von
$$D = T^{-1} \cdot A \cdot T$$
eine Diagonalmatrix ist.
- $A$: Beliebige Matrix
- $B$: Ergebnis einer Transformation der Matrix $A$
- $D$: Ergebnis einer Transformation der Matrix $A$, welche eine Diagonalmatrix ist
- $T$: Beliebige Transformations-Matrix
***Eigenwerte und Eigenvektoren ähnlicher/diagonalisierbarer Matrizen:***
- Es seien $A$ und $B$ zueinander ähnliche Matrizen
- $A$ und $B$ haben dieselben Eigenwerte inkl. deren algebraische Vielfachheit
- Ist $x$ ein Eigenvektor zum Eigenwert $\lambda$ von $B$, so ist $T \cdot x$ ein Eigenvektor zum Eigenwert $\lambda$ von $A$
- Wenn $A$ diagonalisierbar ist gilt zudem folgendes:
- Für $D = T^{-1} \cdot A \cdot T$
- Die $n$ Diagonal-Elemente von $D$ sind die Eigenwerte von $A$
- Die $n$ linear unabhängigen Eigenvektoren von $A$ sind die Spalten des verwendeten $T$
#### $QR$-Verfahren
Das $QR$-Verfahren ist ein iteratives Verfahren zur Bestimmung von Eigenwerten einer Matrix $A$.
Der Vorgang ist dabei folgender:
1. $A_0 = A$
2. $P_0 = I_n$
3. Für $i = 0, 1, 2, \dots, \infin$:
1. $QR$-Zerlegung durchführen: $A_i = Q_i \cdot R_i$
2. $A_{i + 1} = R_i \cdot Q_i$
3. $P_{i + 1} = P_i \cdot Q_i$
4. $P_i$ zurückgeben
***Code-Beispiel:***
```py
from numpy import array, identity, sign, sqrt, square, sum, zeros
def qr(A):
A = array(A)
n = A.shape[0]
R = A.reshape((n, n))
Q = identity(n)
for i in range(n - 1):
I = identity(n - i)
Qi = identity(n)
e = zeros((n - i, 1))
e[0][0] = 1
a = R[i:,i:i + 1]
v = a + sign(a[0]) * sqrt(sum(square(a))) * e
u = (1 / sqrt(sum(square(v)))) * v
H = I - 2 * u @ u.T
Qi[i:,i:] = H
R = Qi @ R
Q = Q @ Qi.T
R[i + 1:,i:i + 1] = zeros((n - (i + 1), 1))
return [Q, R]
def EV(A, iterations):
A = array(A)
n = A.shape[0]
P = identity(n)
for i in range(iterations):
[Q, R] = qr(A)
A = R @ Q
P = P @ Q
return [A, P]
```
### Vektor-Iteration
Die Vektor-Iteration, auch **von-Mises-Iteration** genannt, erlaubt das Bestimmen des grössten Eigenwertes $\lambda$ einer diagonalisierbaren Matrix $A$.
***Spektral-Radius:***
Der Spektral-Radius $\rho(A)$ definiert den höchsten Eigenwert der Matrix $A$:
$$\rho(A) = \max\{|\lambda|\; | \; \lambda \text{ ist ein Eigenwert von }A \in \mathbb{R}^{n \times n}\}$$
Sei $A$ eine diagonalisierbare Matrix mit den Eigenwerten $\lambda_1, \dots, \lambda_n$ wobei $\lambda_1$ betragsmässig am höchsten ist:
$$|\lambda_1| > |\lambda_2| \ge \dots \ge | \lambda_n|$$
Der grösste Eigenwert $\lambda_1$ und der dazugehörige Eigenvektor $v$ lässt sich mit der Vektor-Iteration bestimmen.
Zunächst muss ein beliebiger Startvektor $v_0 \in \mathbb{C}^n$ mit Länge $1$ gewählt werden.
Als nächstes wird für $k = 0, \dots, \infin$ folgendes ausgeführt:
$$v^{(k + 1)} = \frac{A \cdot v^{(k)}}{||A \cdot v^{(k)}||_2}$$
$$\lambda^{(k + 1)} = \frac{(v^{(k)})^T \cdot A \cdot v^{(k)}}{(v^{(k)})^T \cdot v^{(k)}}$$
***Code-Beispiel:***
```py
from numpy import array, linalg
def vectorIteration(A, v, iterations = 10):
l = 0
v = array(v)
v = v.reshape(len(v), 1)
for i in range(iterations):
l = ((v.T @ A @ v) / (v.T @ v)).item()
v = (A @ v) / (linalg.norm(A @ v, ord=2))
print()
print(f"k: {i + 1}")
print(f"x: {v}")
print(f"λ: {l}")
return [v, l]
```
## Formelbuchstaben
- $\alpha$: Lipschitz-Konstante (siehe Fixpunktsatz)
- $[a,b]$: Das Untersuchungs-Interval für den Banachschen Fixpunktsatz
- $A$: Matrix eines linearen Gleichungssystems
- $\tilde{A}$: Umgewandelte Version der Matrix $A$
- $A^T$: Transformierte Matrix $A$
- $b$: Das gewünschte Resultat eines linearen Gleichungssystems
- $B$: Basis der Maschinenzahl
- $e$: Exponent der Maschinenzahl
- $H$: Housholder-Matrix (siehe $QR$-Zerlegung)
- $I$: Identitäts-Matrix (Matrix, überall den Wert $0$ und auf der Diagonalen den Wert $1$ hat)
- $i$: Imaginäre Einheit für die Darstellung komplexer Zahlen
- $j$: Alternative Schreibweise für $i$ in Python und in der Elektrotechnik
- $K$: Konditionszahl
- $L$: Untere Dreiecksmatrix/Normierte Matrix
- $m$: Mantisse (Darstellbarer Bereich der Maschinenzahl)
- $n$: Anzahl möglicher Stellen der Mantisse $m$
- $q$: Konvergenz-Ordnung
- $Q$: Orthogonal-Matrix in der $QR$-Zerlegung
- $R$: Obere Dreiecksmatrix
- $Rg(A)$: Der Rang der Matrix $A$ (Anzahl Zeilen $\not = 0$, die nach Gauss-Elimination übrig bleiben)
- $T$: Transformations-Matrix
- $x$: Darzustellender Wert
- $x_n$: Die $n$-te Approximation von $x$
- $\tilde{x}$: Approximation/Annäherung an $x$
- $\overline{x}$: Exaktes Ergebnis von $x$
- $x^{(k)}$: Die Annäherung von $x$ in der $k$-ten Iteration
- $\lambda$: Eigenwert einer Matrix
- $\rho(A)$: Spektral-Radius der Matrix $A$ (siehe Vektor-Iteration)