# Inhaltsverzeichnis - [Inhaltsverzeichnis](#inhaltsverzeichnis) - [Aussagenlogisches Rechnen](#aussagenlogisches-rechnen) - [Operatoren](#operatoren) - [Regeln](#regeln) - [Regeln der Doppelten Negation](#regeln-der-doppelten-negation) - [Absorption](#absorption) - [Kommutativität](#kommutativität) - [Assoziativität](#assoziativität) - [Distributivität](#distributivität) - [Regeln von De Morgan](#regeln-von-de-morgan) - [Quantoren](#quantoren) - [Regeln](#regeln-1) - [Beweistechniken](#beweistechniken) - [Beweis durch Implikation](#beweis-durch-implikation) - [Beweis durch Widerspruch](#beweis-durch-widerspruch) - [Beweis durch (Gegen-)Beispiel](#beweis-durch-gegen-beispiel) - [Beweis durch Kontraposition](#beweis-durch-kontraposition) - [Beweis durch Äquivalenz](#beweis-durch-äquivalenz) - [Wahrheitstabelle](#wahrheitstabelle) - [Normalformen](#normalformen) - [Negationsnormalform `NNF`](#negationsnormalform-nnf) - [Disjunktive Normalform `DNF`](#disjunktive-normalform-dnf) - [Konjunktive Normalform `KNF`](#konjunktive-normalform-knf) - [Ableitungsbaum](#ableitungsbaum) - [Mengen](#mengen) - [Syntax](#syntax) - [Operationen](#operationen) - [Subset $\subseteq$](#subset-subseteq) - [Vereinigung $\cup$](#vereinigung-cup) - [Schnittmenge $\cap$](#schnittmenge-cap) - [Differenz $\setminus$](#differenz-setminus) - [Komplement/Negation $\overline{A}$](#komplementnegation-overlinea) - [Symmetrische Differenz $\triangle$](#symmetrische-differenz-triangle) - [Mächtigkeit $\vert A \vert$](#mächtigkeit-vert-a-vert) - [Kartesisches Produkt $\times$](#kartesisches-produkt-times) - [Rechenregeln](#rechenregeln) - [Kommuntativität](#kommuntativität) - [Vordefinierte Mengen](#vordefinierte-mengen) - [Potenzmenge $\mathcal{P}$](#potenzmenge-mathcalp) - [Partition](#partition) - [Unendlichkeit](#unendlichkeit) - [Rechnen mit Unendlichkeit](#rechnen-mit-unendlichkeit) - [Relationen](#relationen) - [Äquivalenzklasse](#äquivalenzklasse) - [Äquivalenzrelation](#äquivalenzrelation) - [Themen](#themen) - [Glossar](#glossar) # Aussagenlogisches Rechnen ## Operatoren - $\neg A$ Gesprochen: "Nicht $A$" - $A \wedge B$ Gesprochen: "$A$ und $B$" - $A \vee B$ Gesprochen: "$A$ oder $B$" - $A \Rightarrow B$ Entspricht $\neg A \vee B$. Gesprochen: "$A$ impliziert $B$" - $A \Leftrightarrow B$ Gesprochen: "$A$ äquivalent $B$" ## Regeln ### Regeln der Doppelten Negation $$\neg\neg A \Leftrightarrow A$$ ### Absorption $$A \wedge A \Leftrightarrow A$$ $$A \vee A \Leftrightarrow A$$ ### Kommutativität Operanden können beliebig vertauscht werden: $$A \wedge B \Leftrightarrow B \wedge A$$ $$A \vee B \Leftrightarrow B \vee A$$ ### Assoziativität **Identische** Operationen können in beliebiger Reihenfolge ausgeführt werden: $$(A \wedge B) \wedge C \Leftrightarrow A \wedge (B \wedge C)$$ $$(A \vee B) \vee C \Leftrightarrow A \vee (B \vee C)$$ ### Distributivität **Unterschiedliche** Operationen können "ausmultipliziert" werden: $$A \wedge (B \vee C) \Leftrightarrow (A \wedge B) \vee (A \wedge C)$$ $$A \vee (B \wedge C) \Leftrightarrow (A \vee B) \wedge (A \vee C)$$ ### Regeln von De Morgan $$\neg(A \wedge B) \Leftrightarrow \neg A \vee \neg B$$ $$\neg(A \vee B) \Leftrightarrow \neg A \wedge \neg B$$ ## Quantoren - $\forall x\, A(x)$ Gesprochen: "Für alle $x$ gilt $A(x)$" - $\forall x \in M A(x)$ Gesprochen: "Für alle $x$ aus der Menge $M$ gilt $A(x)$ - $\exists x\, A(x)$ Gesprochen: "Es gibt ein $x$ mit $A(x)$" - $\exists x \in M A(x)$ Gesprochen: "Es gibt ein $x$ aus der Menge $M$ mit $A(x)$" $\forall x \forall y\, A(x,y) \Leftrightarrow \forall{x,y}\, A(x,y)$ und $\exist x \exist y\, A(x,y) \Leftrightarrow \exist{x,y}\, A(x,y)$ > ***Hinweis:*** > Die Bezeichnung fär die Symbole $\forall$ und $\exist$ sind _Allquantor_ und _Existenzquantor_. ### Regeln - Vertauschungsregel für unbeschränkte Quantoren $\forall x\, A(x) \Leftrightarrow \neg\exist x\, \neg A(x)$ - Vertauschungsregel für beschränkte Quantoren $\forall x \in K\, A(x) \Leftrightarrow \neg\exist x \in K \neg A(x)$ - Beschränkter und unbeschränkter Allquantor $\forall x \in K A(x) \Leftrightarrow \forall x(x \in K \Rightarrow A(x))$ - Beschränkter und unbeschränkter Existenzquantor $\exist x K A(x) \Leftrightarrow \exist x(x \in K \wedge A(x))$ # Beweistechniken ## Beweis durch Implikation Anwendbar bei Formeln in der Form: $$A \Rightarrow B$$ 1. Zwingende Voraussetzungen für die Bedingung $A$ erfassen 2. Prüfen, ob $B$ richtig ist > ***Beispiel:*** > $A$: "$x$ und $y$ sind gerade." > $B$: "$x \cdot y$ ist gerade." > > Damit $x$ und $y$ gerade sind, müssen sie ein Produkt von $2$ sein. Die Behauptung ist also: > > $x = 2 \cdot n_x$ und $y = 2 \cdot n_y$ > > $n_x$ und $n_y$ sind hierbei **beliebige** natürliche Zahlen. > > Für den Nachweis ergibt sich folgendes für $B$: > $$x \cdot y = (2 \cdot n_x) \cdot (2 \cdot n_y) = 22 \cdot (n_x \cdot 2 \cdot n_y)$$ > Da das Ergebnis ein vielfaches von $2$ ist, heisst das, dass $x \cdot y$ gerade ist und somit die Aussage $A \Rightarrow B$ wahr ist. ## Beweis durch Widerspruch Anwendbar bei einfachen Aussagen. Der Merksatz ist hierbei: "Wenn die Aussage _nicht nicht wahr_ ist, ist sie _wahr_." Der Vorgang ist hierbei, die ursprüngliche Aussage zu negieren und zu beweisen, dass die negierte Aussage **unerfüllbar** ist. > ***Beispiel:*** > $A$: "Es gibt keine grösste natürliche Zahl." > $\neg A$: "Es gibt **eine** grösste natürliche Zahl." > > $m$ sei dei grösste natürliche Zahl. Für jede natürliche Zahl $x$ gibt es ein Inkrement, welches man mit Hilfe von $x + 1$ errechnen kann. So gibt es auch für $m$ ein Inkrement $m + 1$, welches um $1$ grösser ist als $m$. Somit sit die negierte Aussage $\neg A$ **unerfüllbar**. $A$ ist wahr. ## Beweis durch (Gegen-)Beispiel Anwendbar bei Aussagen mit Quantoren ($\forall$ "für alle" und $\exists$ "existiert"). Die Strategie hierbei ist, ein anwendbares Beispiel (im Falle $\exists$) oder Gegenbeispiel (im Falle $\forall$) zu finden. > ***Beispiel:*** > $A$: "Es existieren Zahlen, welche kein Quadrat einer natürlichen Zahl sind." > > Dies lässt sich an dem Beispiel $2$ beweisen. $2$ ist weder ein Quadrat von $1$ ($1^2 = 1$) noch von $2$ ($2^2 = 4)$. ## Beweis durch Kontraposition Anwendbar bei Aussagen in der Form $A \Rightarrow B$ Es gilt für diese Strategie, die dazugehörige Kontraposition $\neg B \Rightarrow \neg A$ zu belegen. > ***Beispiel:*** > $A$: "Für jede natürliche Zahl $n$ gilt: $(n^2 + 1 = 1) \Rightarrow (n = 0)$ > > Die Kontraposition dazu lautet wie folgt: > $A'$: "Für alle Zahlen, die **nicht** $0$ sind gilt $n^2 + 1 \not= 1$ > > Da alle Zahlen $> 0$ ein Quadrat haben, das grösser als $0$ ist, gilt: $n^2 + 1 > 1$. > Daraus folgt, dass Aussage $A$ wahr ist. ## Beweis durch Äquivalenz Anwendbar für Aussagen der Form $A \Leftrightarrow B$ Die Strategie ist hierbei, zu beweisen, dass $A \Rightarrow B$ gilt und $B \Rightarrow A$ gilt. > ***Beispiel:*** > $A: (n^2 + 1 = 1) \Leftrightarrow (n = 0)$ > > Wenn $n = 0$ ist, ergibt sich aus $(n^2 + 1 = 1)$ folgendes: $(0^2 + 1 = 1) = (0 + 1 = 1)$. Damit ist $A \Rightarrow B$ bewiesen. > > Die einzige Situation in der $(n^2 + 1 = 1)$ oder eher $(n^2 = 0)$ ergibt, ist, wenn $n$ $0$ entspricht. Damit ist auch $B \Rightarrow A$ bewiesen. ## Wahrheitstabelle Folgend ein Beispiel einer Wahrheitstabelle: | $a$ | $b$ | $c$ | $b \vee c$ | $a \Rightarrow (b \vee c)$ | | :---: | :---: | :---: | :--------: | :------------------------: | | $0$ | $0$ | $0$ | $0$ | $1$ | | $0$ | $0$ | $1$ | $1$ | $1$ | | $0$ | $1$ | $0$ | $1$ | $1$ | | $0$ | $1$ | $1$ | $1$ | $1$ | | $1$ | $0$ | $0$ | $0$ | $0$ | | $1$ | $0$ | $1$ | $1$ | $1$ | | $1$ | $1$ | $0$ | $1$ | $1$ | | $1$ | $1$ | $1$ | $1$ | $1$ | ## Normalformen Normalformen beinhalten generell nur `AND`s ($\wedge$), `OR`s ($\vee$) und `NOT`s ($\neg$) ### Negationsnormalform `NNF` Die Negationsnormalform (`NNF`) ist die Form einer Formel, in der nur atomare (nicht aufteilbare) Teilformeln negiert sind. > ***Beispiel:*** > $$(A \wedge (\neg B \vee (C \vee D)))$$ > Merke, dass nur $B$, welches _atomar_ ist, negiert ist. ### Disjunktive Normalform `DNF` Die Disjunktive Normalform ist eine Umformung der Formel, in der alle Belegungen für die die Formel $true$ ergibt, mit einander "verodert" werden. > ***Beispiel:*** > Die `DNF` für die Formel $\neg A \wedge (B \vee C)$ lautet folgendermassen: > > $$(\neg A \wedge \neg B \wedge C) \vee (\neg A \wedge B \wedge \neg C) \vee (\neg A \wedge B \wedge C)$$ > > ***Herleitung:*** > Schritt 1: Wahrheitstabelle aufstellen: > | $A$ | $B$ | $C$ | $B \vee C$ | $\neg A \wedge (B \vee C)$ | > | :---: | :---: | :---: | :--------: | :------------------------: | > | $0$ | $0$ | $0$ | $0$ | $0$ | > | $0$ | $0$ | $1$ | $1$ | $1$ | > | $0$ | $1$ | $0$ | $1$ | $1$ | > | $0$ | $1$ | $1$ | $1$ | $1$ | > | $1$ | $0$ | $0$ | $0$ | $0$ | > | $1$ | $0$ | $1$ | $1$ | $0$ | > | $1$ | $1$ | $0$ | $1$ | $0$ | > | $1$ | $1$ | $1$ | $1$ | $0$ | > > Schritt 2: $1$-Stellen aufschreiben: > - $\neg A \wedge \neg B \wedge C$ > - $\neg A \wedge B \wedge \neg C$ > - $\neg A \wedge B \wedge C$ > > Schritt 3: Formeln für $1$-Stellen "verodern": > $$(\neg A \wedge \neg B \wedge C) \vee (\neg A \wedge B \wedge \neg C) \vee (\neg A \wedge B \wedge C)$$ ### Konjunktive Normalform `KNF` Bei der Konjunktiven Normalform wiederum, werden alle negierten Belegungen, in denen die gegebene Formel $false$ ergibt miteinander "geandet". > ***Beispiel:*** > Der `KNF` von $B \vee (A \wedge C)$ ist: > $$(A \vee B \vee C) \wedge (A \vee B \vee \neg C) \wedge (\neg A \vee B \vee C)$$ > > ***Herleitung:*** > Schritt 1: Wahrheitstabelle aufstellen: > | $A$ | $B$ | $C$ | $A \vee C$ | $B \vee (A \wedge C)$ | > | :---: | :---: | :---: | :--------: | :-------------------: | > | $0$ | $0$ | $0$ | $0$ | $0$ | > | $0$ | $0$ | $1$ | $0$ | $0$ | > | $0$ | $1$ | $0$ | $0$ | $1$ | > | $0$ | $1$ | $1$ | $0$ | $1$ | > | $1$ | $0$ | $0$ | $0$ | $0$ | > | $1$ | $0$ | $1$ | $1$ | $1$ | > | $1$ | $1$ | $0$ | $0$ | $1$ | > | $1$ | $1$ | $1$ | $1$ | $1$ | > > Schritt 2: $0$-Stellen aufschreiben **und negieren**: > - $\neg A \wedge \neg B \wedge \neg C$ > Negation: $A \vee B \vee C$ > - $\neg A \wedge \neg B \wedge C$ > Negation: $A \vee B \vee \neg C$ > - $A \wedge \neg B \wedge \neg C$ > Negation: $\neg A \vee B \vee C$ > > Schritt 3: Negierte Ausdrücke mit `AND`s verketten: > $$(A \vee B \vee C) \wedge (A \vee B \vee \neg C) \wedge (\neg A \vee B \vee C)$$ ## Ableitungsbaum Der Ableitungsbaum bietet einen übersichtlichen Weg um Gleichungen in der Aussagenlogik zu lösen. Folgend ein Beispiel: Es sei $(x \Rightarrow y) \wedge z$ mit folgender Belegung: - $B(x) = \top$ - $B(y) = \bot$ - $B(z) = \top$ Der dazugehörige Ableitungsbaum ist dann: ```mermaid flowchart BT op3(("∧: 0")) op2(("∨: 0")) op1(("¬: 0")) x["x: 1"] y["y: 0"] z["z: 1"] x --- op1 op1 --- op2 y --- op2 op2 --- op3 z --- op3 ``` # Mengen Mengen haben keine Sortierung und keine doppelten Elemente. > ***Hinweise:*** > - Mengen heissen "disjunkt", wenn sie **keine gemeinsamen** Elemente beinhalten. ## Syntax $M = \{ x \in \N | x > 5\}$ - $\in$ Gesprochen: "Element von" - $\notin$ Gesprochen: "Nicht Element von" - $|$ Gesprochen: "Für die gilt" "$M$ ist die Menge aller $x$, für die gilt, dass $x > 5$ ist." $M = { 5, 6, 7, 8, ... 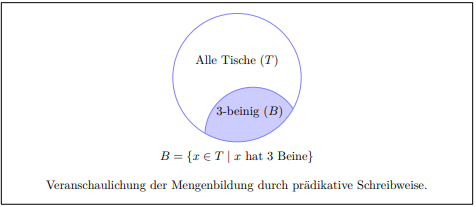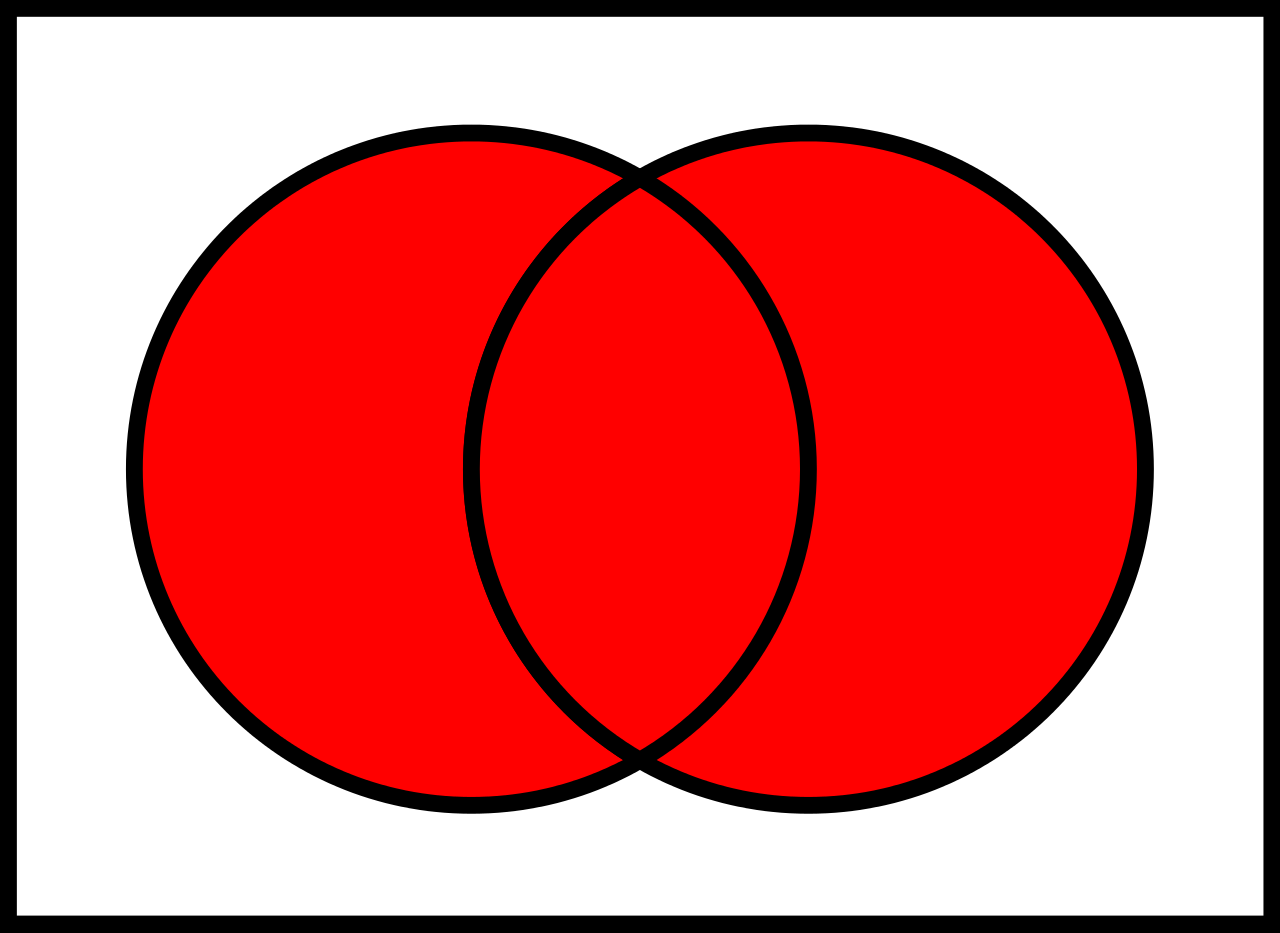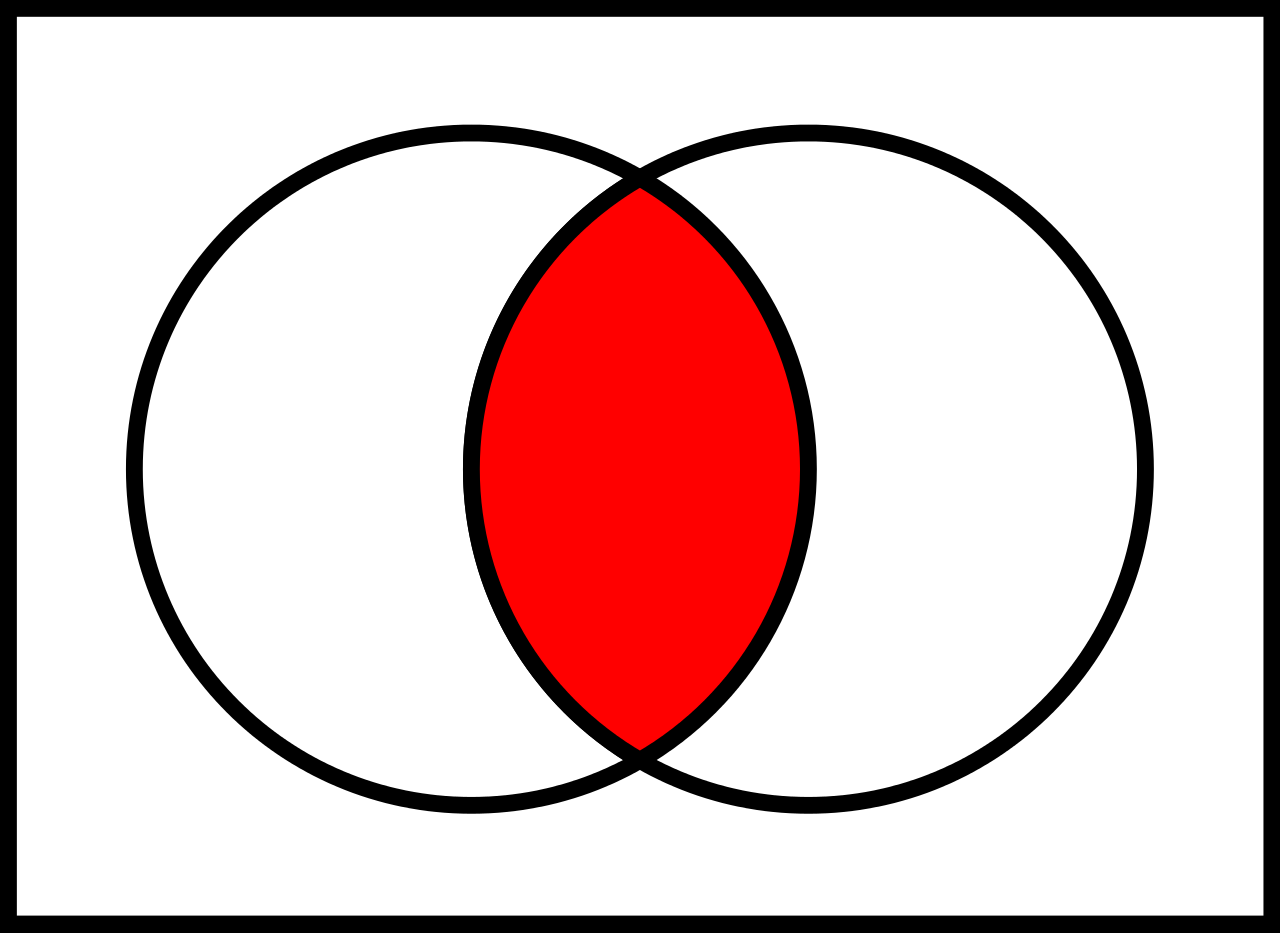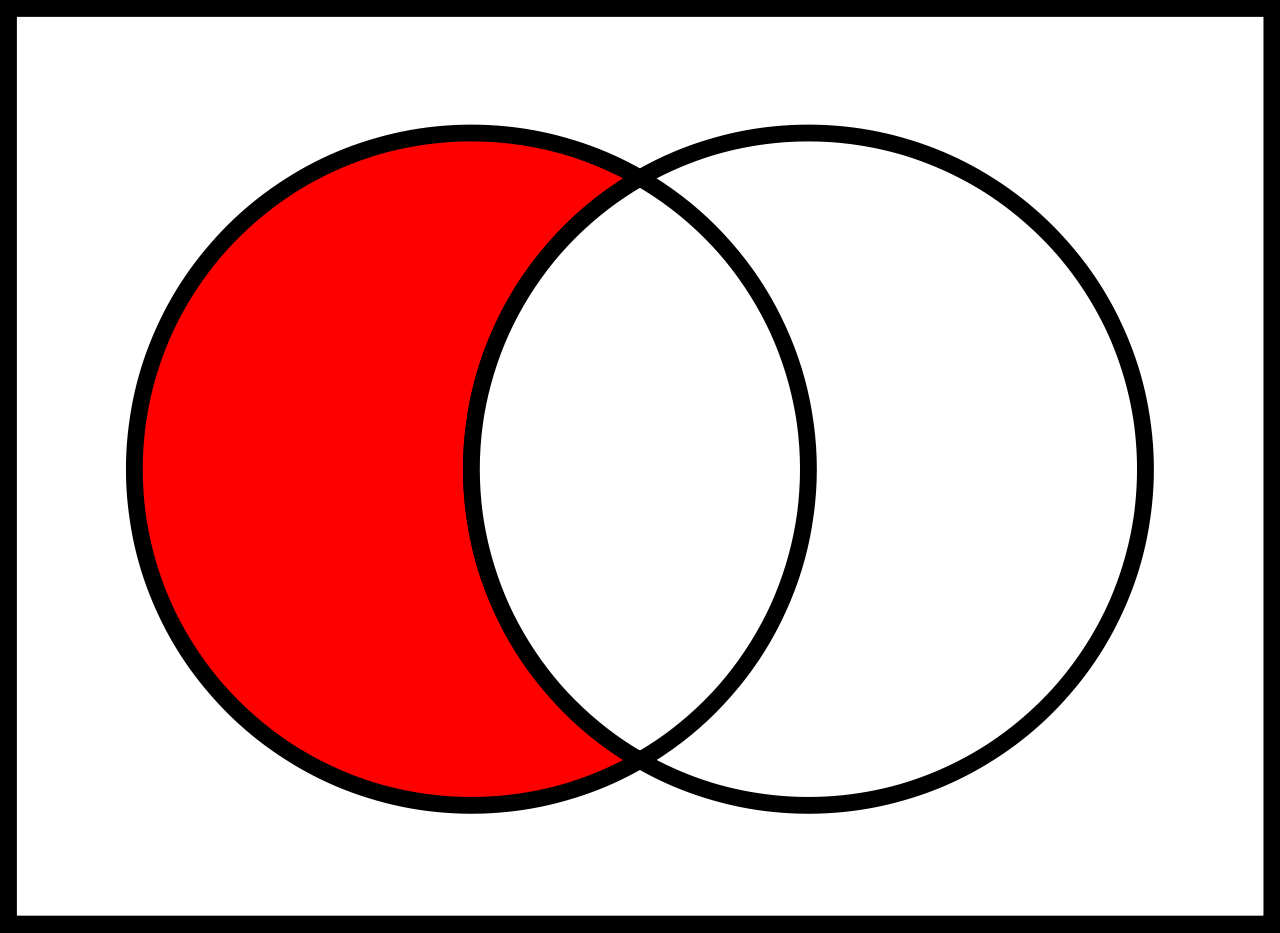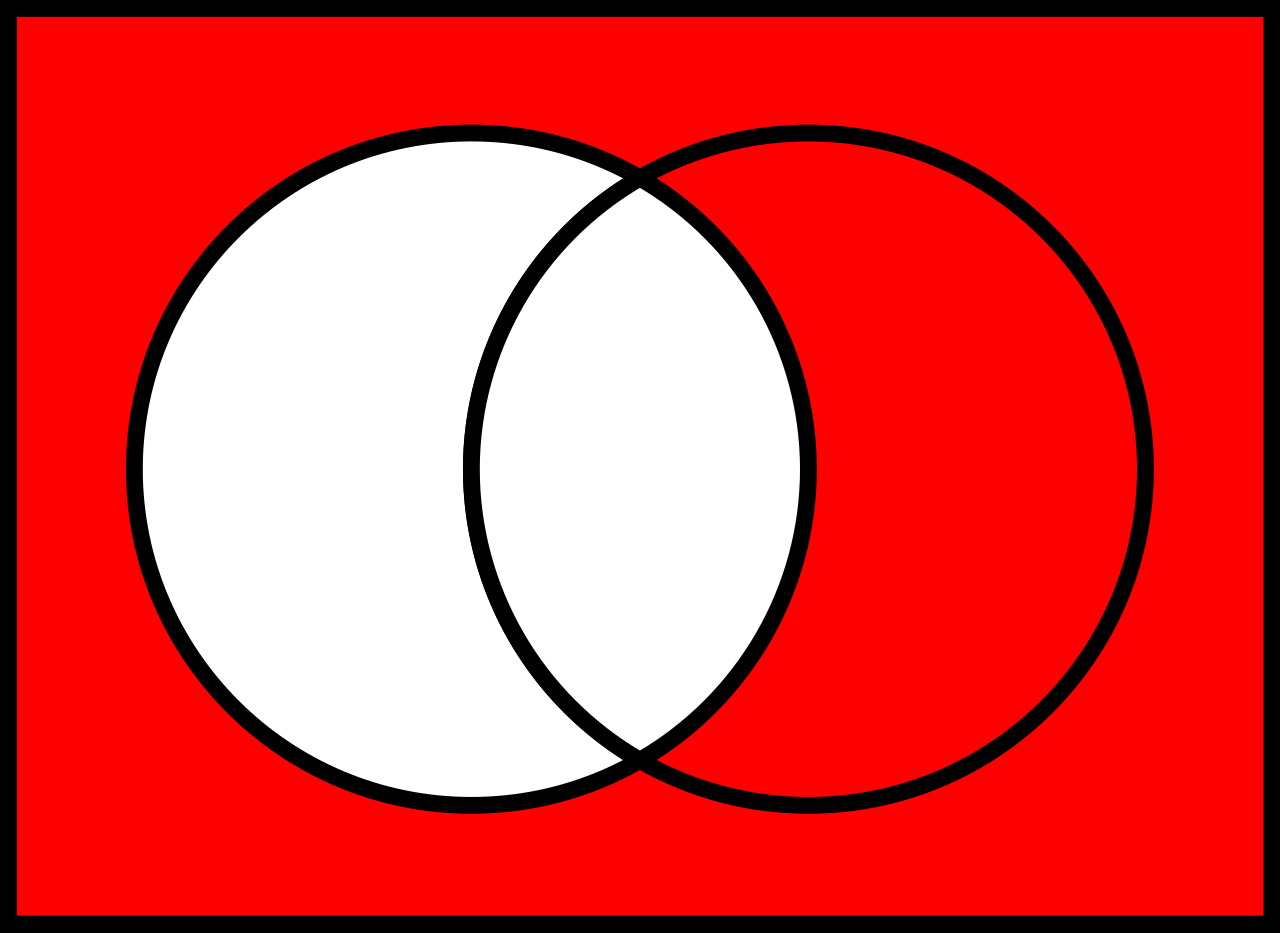}$  ## Operationen ### Subset $\subseteq$ ### Vereinigung $\cup$ Die Vereinigung "Union" beschreibt die Zusammenfassung zweier Mengen:  ### Schnittmenge $\cap$ Die Schnittmenge "Intersection" zweier Mengen:  ### Differenz $\setminus$ Beschreibt die Differenzmenge zweier Mengen:  $A \setminus B$ gesprochen: "$A$ ohne $B$" ### Komplement/Negation $\overline{A}$ Das Komplement einer Menge $A$ wird wie folgt geschrieben: $$\overline{A}$$ Sie beschreibt alle Elemente, die _nicht_ in der Menge $A$ vorkommen:  ### Symmetrische Differenz $\triangle$ Die Vereinigung zweier Mengen abzüglich deren Schnittmenge:  $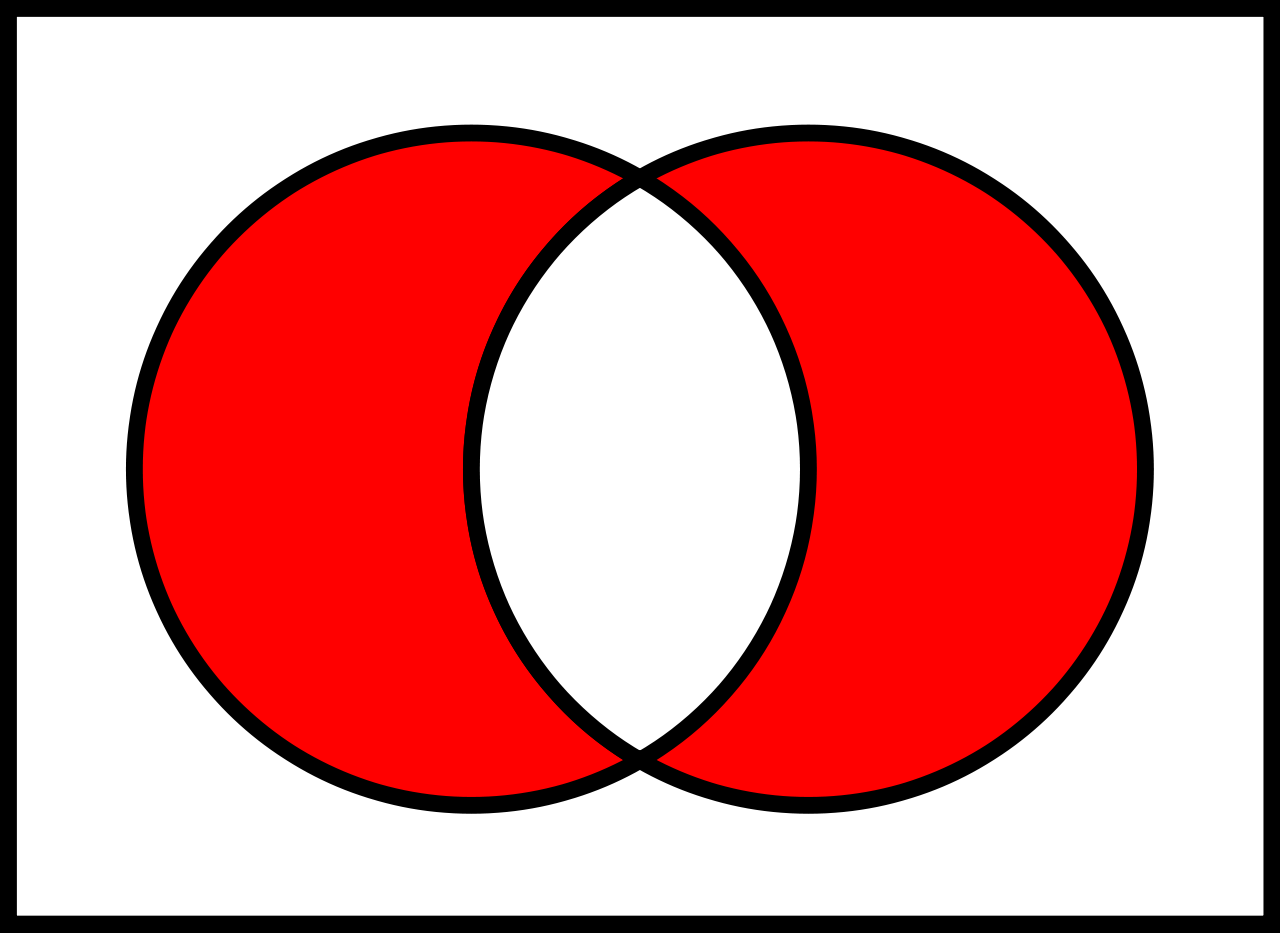A \triangle B = (A \setminus B) \cup (B \setminus A)$ gesprochen "$A$ ohne $B$ vereinigt mit $B$ ohne $A$" ### Mächtigkeit $\vert A \vert$ Die Mächtigkeit $\vert A \vert$ beschreibt, wieviele Elemente eine Menge $A$ beinhaltet. > ***Beispiel:*** > $\vert \{1, 78, 28\} \vert = 3$ ### Kartesisches Produkt $\times$ Das Kartesische Produkt ist eine Menge aller Folgen, die aus den Elementen der beiden Mengen gebildet werden können. Beispiel: $$A = \{a, b\}$$ $$B = \{2, 3, 4\}$$ $$A \times B = \{a, b\} \times \{2, 3, 4\} = \{(a, 2), (a, 3), (a, 4), (b, 2), (b, 3), (b, 4)\}$$ Die Mächtigkeit von $A \times B$ ist gleich $\vert A \vert \cdot \vert B \vert$ > ***Hinweis:*** > **Folgen** sind sortiert das bedeutet folgendes: > $$A \times B \not = B \times A$$ ## Rechenregeln ### Kommuntativität ## Vordefinierte Mengen - $\N$: Natürliche Zahlen - Zahlen $\geq 0$ - $\Z$: Alle ganzen Zahlen (positiv und negativ) ## Potenzmenge $\mathcal{P}$ Die Potenzmenge gibt alle möglichen Kombinationen aus einer gegebenen Menge zurück. Die Funktion $\mathcal{P}(x)$ ist folgendermassen definiert: $$\mathcal{P}(A) := \{x | x \subseteq A \}$$ > ***Beispiel:*** > $$\mathcal{P}(\{0, 1\}) = \{\emptyset, \{0\}, \{1\}, \{0, 1\}\}$$ > ***Bemerkung:*** > Die Mächtigkeit einer Potenzmenge errechnet sich folgendermassen: > $$|\mathcal{P}(A)| = 2^{|A|}$$ ## Partition Eine Partition einer Menge $A$ ist eine Menge von Teilmengen von $A$. Diese Teilmengen müssen folgende Bedingungen erfüllen: - Die Mengen dürfen nicht leer sein - Teilmengen dürfen untereinander keine gemeinsamen Elemente haben ## Unendlichkeit Unendliche Mengen sind unter folgenden Bedingungen abzählbar oder überabzählbar: - Abzählbar unendlich, wenn sie gleich mächtig wie $\N$ sind - Überabzählbar unendlich, wenn sie mächtiger als $\N$ sind ### Rechnen mit Unendlichkeit $A$ sei eine abzählbar unendliche und $B$ eine überabzählbar unendliche Menge: - $A \cup B$ ist **abzählbar**, da im Ergebnis nur Elemente aus der abzählbaren Menge $A$ enthalten sind. - $A \cap B$ ist **überabzählbar**, da alle Elemente der überabzählbaren Menge $B$ im Ergebnis enthalten sind - $B \setminus A$ ist **überabzählbar**, da von der überabzählbaren Menge $B$ nur die abzählbaren Elemente abgezogen werden. 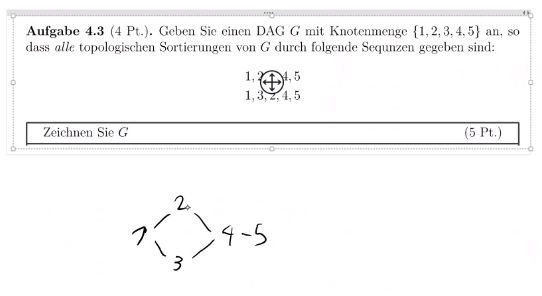# Relationen DAG ("discrete acyclic graph") ein "gerichteter azyklischer Graph" ist ein Graph, in dem keine Zyklen enthalten sind: Folgendes ist ein DAG: ```mermaid flowchart LR a((A)) b((B)) c((C)) d((D)) e((E)) f((F)) g((G)) a --> b b --> c c --> e b --> e b --> d g --> d d --> e e --> f ``` Folgendes ist **kein** DAG: ```mermaid flowchart LR a((A)) b((B)) c((C)) d((D)) e((E)) f((F)) a --> b b --> c d --> b c --> e e --> f e --> d ``` ## Äquivalenzklasse Eine Äquivalenzklasse beinhaltet alle Elemente, welche einer Klasse zugeordnet werden können  ## Äquivalenzrelation # Themen - Chinesischer Restsatz - Euklidischer Algorithmus (ggt, kgv berechnen)  # Glossar | Bezeichnung | Beschreibung | | -------------------- | ------------------------------------------------------------------ | | Knotenmenge | Die Menge aller Elemente (Knoten), die in einem Graphen vorkommen. | | Wahrheits-Konstanten | $\top$ steht für `true`, $\bot$ für `false`.