# Zusammenfassung Analysis 2
## Nullstellen durch Horner-Schema
Das Horner-Schema erlaubt es, Nullstellen leicht zu bestimmen.
Der Vorgang wird anhand der folgenden Gleichung aufgezeigt:
$$f(x) = 3x^3 - 15x + 12$$
Eine Nullstelle dieser Formel ist die $1$. Dies lässt sich wie folgt mit dem Horner-Schema prüfen:
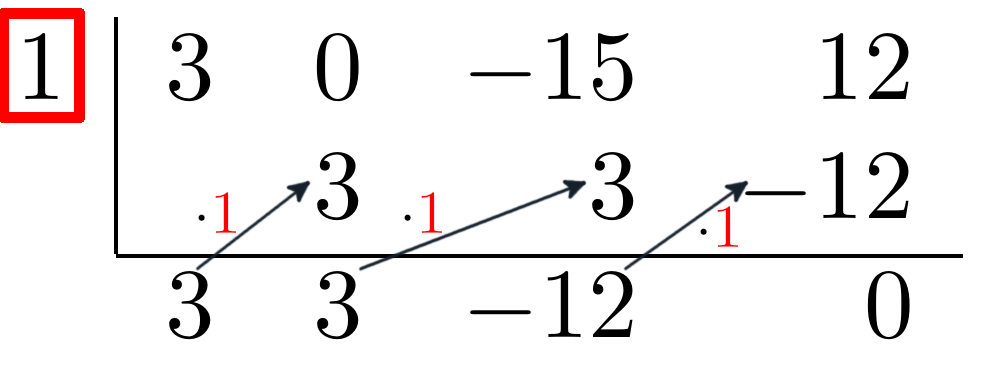
**1. Nullstelle aufschreiben**
Im Bild rot markiert
**2. Die Koeffizienten aller $x$-Potenzen aufschreiben**
Zu sehen im Bild in der obersten Reihe.
Entspricht eine der Koeffizienten $0$ (wie in diesem Beispiel $x^2$), so **muss** im Horner-Schema eine $0$ eingetragen werden.
**4. Startwert notieren**
Die Berechnung wird gestartet indem man den ersten Koeffizient (in diesem Fall $3$) in die unterste Reihe überträgt.
**5. Berechnung**
In diesem Schritt multipliziert man die Eingabe-Zahl mit der bekannten Nullstelle (im Bild durch graue Pfeile markiert) und addiert das Ergebnis mit dem nachfolgenden Koeffizienten.
Ist das letzte Resultat $0$, so handelt es sich auch wirklich um eine Nullstelle.
> **Note:**
> Anhand der Resultat-Reihe im Horner-Schema lässt sich das übrigbleibende Polynom ablesen.
>
> Rechnet man die Nullstelle $1$ aus der Rechnung $3x^3 - 15x + 12$ heraus, so würde das übrigbleibende Polynom folgendermassen lauten:
> $$3x^2 + 3x - 12$$
>
> Verdeutlicht:
> $$3x^3 - 15x + 12 = (x - 1) \cdot (3x^2 + 3x - 12)$$
## Stammfunktion
Umkehrung von Ableitungen gemäss der Seite über Ableitungen.
Alle Ableitungsregeln können unter Ableitungen nachgeschlagen werden.
## Integrale
Integrale erlauben es, die Fläche unter Funktionen zu berechnen:
**Beispiel anhand der Funktion $f(x) = x^3 + 5$**
Integrale haben folgende Erscheinungsform:
$$\int_{a}^{b}{f(x)}dx$$
Die Zeichen haben folgende Bedeutung:
- $\int$: Integrations-Zeichen
- $a$: Die Untergrenze (Punkt ab dem integriert werden soll)
- $b$: Die Obergrenze (Punkt bis zu dem integriert werden soll)
- $f(x)$: Zu integrierende Funktion
- $dx$: Bezeichnet, dass $x$ integriert wird, indem unendlich kleine Rechtecke aufsummiert werden.
### Grundintegrale
$$\begin{aligned}
\int{a}dx &= ax \\
\int{x^n}dx &= \frac{x^{n+1}}{n + 1}, &n &\not = -1 \\
\int{\frac{1}{x}}dx &= \ln(|x|), &x &\not = 0 \\
\int{a^x}dx &= \frac{a^x}{\ln(a)}, &a &> 0, &a &\not = 1
\end{aligned}$$
### Integration von Produkten
Produkte benötigen zum Teil spezielle Vorgehensweisen um sie zu integrieren.
Zwei gängige Wege dazu sind im Folgenden Beschrieben.
#### Integration durch Substitution
Die Integration durch Substitution basiert auf der folgenden Regel:
$$\int_a^b{f(u(x)) \cdot u'(x)}dx = \int_{u(a)}^{u(b)}{f(u)}du$$
Die Integration durch Substitution wird hier anhand des folgenden Beispiels gezeigt:
$$\int_0^{\sqrt{\frac{\pi}{2}}}{\cos(x^2) \cdot x}dx$$
**1. Funktionen bestimmen**
Im Folgenden werden die Haupt- und die Unterfunktion bestimmt.
- $u(x) = x^2$
- $g(x) = \cos(u)$
- $f(x) = g(u(x))$
**2. Substitutions-Gleichung für $dx$**
Diese kann mit folgender Regel ermittelt werden:
$$\frac{du}{dx} = u'(x) \Rightarrow dx = \frac{du}{u'(x)}$$
Das ergibt in diesem Beispiel folgendes:
$$\frac{du}{dx} = u'(x) = 2x \Rightarrow dx = \frac{du}{2x}$$
**3. Substitution**
Nun müssen die errechneten Werte in die folgende Formel eingesetzt werden:
$$\int_{u(a)}^{u(b)}{f(u)}du$$
Wobei $du$ durch unser errechnetes $dx$ ersetzt werden muss.
Wichtig ist hierbei, dass sich $x$ komplett wegkürzen lassen **muss**.
$$\int_0^{\sqrt{\frac{\pi}{2}}}{\cos(x^2) \cdot x}dx =
\int_{u(0)}^{u(\sqrt{\frac{\pi}{2}})}{\cos(u) \cdot x \cdot \frac{du}{2x}}$$
Vereinfacht ergibt das folgendes:
$$\int_0^{\frac{\pi}{2}}{\frac{1}{2} \cdot \cos(u)}du = \left[\frac{1}{2} \cdot \sin(u)\right]_0^{\frac{\pi}{2}}$$
**4. Resultat berechnen**
$$\left[\frac{1}{2} \cdot \sin(u)\right]_0^{\frac{\pi}{2}} = \left(\frac{1}{2} \cdot 1\right) - \left(\frac{1}{2} \cdot 0\right) = \frac{1}{2}$$
Bei Integralen, die keine Grenzen definiert haben, lässt sich das Ergebnis nicht eindeutig bestimmen.
Hätte das ursprüngliche Integral keine Grenzen, wäre das Ergebnis folgendes:
$$\left[\frac{1}{2} \cdot \sin(u)\right] = \frac{1}{2} \cdot \sin(u) + C$$
**5. Rücksubstitution**
Im Falle eines Integrals ohne Grenzen muss die Variable $u$ rück-substituiert werden:
$$\frac{1}{2} \cdot \sin(u) + C = \frac{1}{2} \cdot \sin(x^2) + C$$
#### Partielle Integration
Die Partielle Integration beruht auf folgender Regel:
$$\int_a^b{u'(x) \cdot v(x)dx} = \left[u(x) \cdot v(x)\right]_a^b - \int_a^b{u(x) \cdot v'(x)}dx$$
Die Partielle Integration wird anhand des folgenden Beispiels erklärt:
$$\int_0^\pi{sin(x) \cdot x}dx$$
Folgende Schritte müssen für die partielle Integration durchgeführt werden:
**1. Unterfunktionen bestimmen**
Einem Teil der Funktion $v$ und einem anderen $u'$ zuordnen. Sollte die partielle Integration nicht funktionieren, kann in diesem Schritt die Zuordnung von $v$ und $u'$ vertauscht werden.
- $u'(x) = sin(x)$
- $v(x) = x$
**2. Stammfunktion von $u'$ und Ableitung von $v$ bestimmen**
- $u(x) = -\cos(x)$
- $v'(x) = 1$
**3. Resultat berechnen**
Daraus ergibt sich folgende Gleichung:
$$\int_0^\pi{u'(x) \cdot v(x)dx} = \left[u(x) \cdot v(x)\right]_0^\pi - \int_0^\pi{u(x) \cdot v'(x)}dx$$
$$\left[-\cos(x) \cdot x\right]_0^\pi - \int_0^\pi{-\cos(x) \cdot 1}dx$$
$$((1 \cdot \pi) - (1 \cdot 0)) - \int_0^\pi{-\cos(x)}dx$$
$$(\pi - 0) - \left[\sin(x)\right]_0^\pi$$
$$(\pi - 0) - (\sin(0) - \sin(\pi))$$
$$(\pi - 0) - (0 - 0) = \pi$$
> **Note:**
> Die Partielle Integration kann auch für einfache Operationen verwendet werden, indem eine Multiplikation mit $1$ durchgeführt wird.
>
> Beispiel:
>
> $$\int{ln(x)}dx = \int{ln(x) \cdot 1}dx$$
#### Partialbruchzerlegung
Für die Partialbruchzerlegung muss der zu integrierende Bruch **vollständig gekürzt** sein.
Die Partialbruchzerlegung wird anhand der folgenden Aufgabe erklärt:
$$\int{\frac{x + 1}{x^3 + 5x^2 + 8x - 4}}dx$$
Folgende Schritte müssen durchgeführt werden:
**1. Nullstellen des Nenners bestimmen**
Durch erraten: (Eine der Nullstellen ist $1$)
Linearfaktor abspalten mit Horner-Schema:
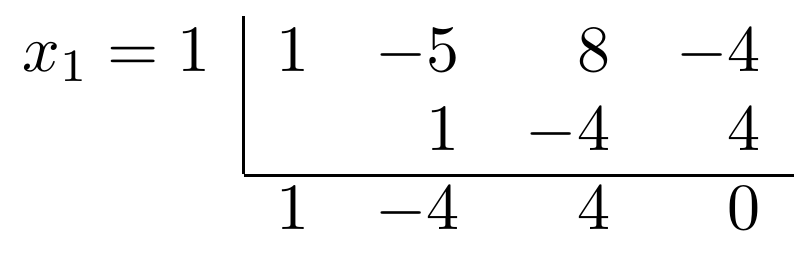
Verbleibendes Polynom: $x^2 - 4x + 4 = (x - 2) \cdot (x - 2)$
Die verbleibende, **doppelte** Nullstelle ist also $x = 2$.
**2. Jeder Nullstelle eine Summe von Nullstellen zuordnen**
- Für einfache Nullstellen:
$$\rightarrow \frac{A}{x - x_1}$$
- Für doppelte Nullstellen:
$$\rightarrow \frac{A_1}{x - x_1} + \frac{A_2}{(x - x_1)^2}$$
- Für $r$-fache Nullstellen:
$$\rightarrow \frac{A_1}{x - x_1} + \frac{A_2}{(x - x_1)^2} + ... + \frac{A_r}{(x - x_1)^r}$$
Das ergibt im Fall des Beispiels folgendes:
$$\frac{x + 1}{x^3 - 5x^2 + 8x - 4} = \frac{A}{x - 1} + \frac{B}{x - 2} + \frac{C}{(x - 2)^2}$$
**3. Brüche gleichnamig machen**
$$\frac{x + 1}{(x - 1)(x - 2)^2} = \frac{A(x - 2)^2}{(x + 1)(x - 2)^2} + \frac{B(x - 1)(x - 2)}{(x + 1)(x - 2)^2} + \frac{C(x - 1)}{(x + 1)(x - 2)^2}$$
Da die Brüche nun gleichnamig sind, können sämtliche Nenner weggekürzt werden:
$$x + 1 = A(x - 2)^2 + B(x - 1)(x - 2) + C(x - 1)$$
**4. Koeffizienten mit Hilfe von LGS ausrechnen**
Gleichung ausmultiplizieren und nach Potenz zerlegen:
$$(A + B)x^2 + (C - 4A - 3B)x + (4A + 2B - C)$$
- $x + 1$ beinhaltet kein $x^2$. Also muss $(A + B)$ zwingend $0$ ergeben:
$$A + B = 0$$
- $x + 1$ beinhaltet $1x$. Also muss $C - 4A - 3B$ $1$ ergeben:
$$C - 4A - 3B = 1$$
- $x + 1$ beinhaltet eine Konstante $1$. Also muss $4A + 2B - C$ $1$ ergeben:
$$4A + 2B - C = 1$$
Das Lösen des Gleichungssystems ergibt folgende Resultate:
- $A = 2$
- $B = -2$
- $C = 3$
Daraus ergibt sich folgendes:
$$\frac{x + 1}{(x - 1)(x - 2)^2} = \frac{2}{x - 1} + \frac{-2}{x - 2} + \frac{3}{(x - 2)^2}$$
**5. Integration der Teilbrüche**
Für Nenner ohne Exponent:
$$\int{\frac{1}{x - x_0}}dx = \int{\frac{1}{u}}du = \ln(|u|) + c = \ln(|x - x_0|) + c$$
Für Nenner mit Exponent:
$$\begin{split}
\int{\frac{1}{(x - x_0)^r}}dx = \int{u^{-r}}du & = \frac{u^{-r + 1}}{-r + 1} + c \\
& = \frac{(x - x_0)^{-r + 1}}{1 - r} + c \\
& = \frac{1}{(1 - r)(x - x_o)^{r - 1}} + c
\end{split}$$
Für das aktuelle Beispiel ergibt das folgendes:
$$\begin{split}
\int{\frac{2}{x - 1} + \frac{2}{x - 2} + \frac{3}{(x - 2)^2}}dx & = \int{\frac{2}{x - 1}} - \int{\frac{2}{x - 2}} + \int{\frac{3}{(x - 1)^2}} \\
& = 2 \cdot \int{\frac{1}{x - 1} - 2 \cdot \int{\frac{1}{x - 2}}} + 3 \cdot \int{\frac{1}{(x - 2)^2}} \\
& = 2 \cdot \ln(|x - 1|) - 2 \cdot \ln(|x - 2|) - 3 \cdot \frac{1}{x - 2} + c
\end{split}$$
#### Leitfaden

## Uneigentliche Integrale
Uneigentliche Integrale sind Integrale, welche einen unendlich grossen Integrationsbereich hat oder eine Polstelle (Grenze an unendlichem Wert) enthält.
### Uneigentlicher Integrationsbereich
Dies ist der Fall, wenn die Untergrenze eines Integrals $-\infin$ oder dessen Obergrenze $+\infin$ ist.
_Beispiel anhand des Integrals $\int_1^{\infin} 6 \cdot \frac{1}{x^2}$_
Uneigentliche Integrale können berechnet werden, indem man erst die Stammfunktion ausformuliert, um dann den Grenzwert zu berechnen.
**1. Bestimmung der Stammfunktion**
$$\int_1^{\infin}{6 \cdot \frac{1}{x^2}} = \left[6 \cdot -\frac{1}{x}\right]_1^{\infin}$$
**2. Grenzwert mit Hilfe von $\lim$ berechnen**
$$\left[6 \cdot -\frac{1}{x}\right]_1^{\infin} = 6 \cdot -\frac{1}{\infin} - 6 \cdot -\frac{1}{1} = 6 \cdot 0 - -6 \cdot -1 = 6$$
## Differentialgleichungen
### Gewöhnliche Differentialgleichungen
Differentialgleichungen sind Funktionen, welche als Rückgabewert an Stelle eines Skalar-Werts eine Funktion liefert.
Eine Differentialfunktion wird dargestellt durch die Ableitung, die resultierende Funktionen haben sollen:
So sind für die Differenzialgleichung $y' = x - y + 1$ alle resultierende Funktionen gültig, welche die Ableitung $x - y + 1$ haben.
Die Ordnung einer Differentialgleichung sagt aus, was der höchste Ordnung der höchsten vorkommenden Ableitung.
### Differentialgleichungen 1. Ordnung
Differentialgleichungen 1. Ordnung lassen sich als Richtungsfelder darstellen:
Obig zu sehen ist das Richtungsfeld für die Differentialgleichung $y' = x - y + 1$.
Die Striche zeigen jeweils die Steigung, die das Resultate der Differentialgleichung mit dem entsprechenden $x$- und $y$-Wert hat.
Hierbei steht $0$ für keine Steigung (waagerecht), -1 für eine 45°-Senkung nach unten und 1 für eine 45°-Steigung nach oben.
Alternativ lässt sich die Differentialgleichung auch in tabellarischer Form für $y'$ darstellen:
| $f'(x_0, y_0)$ | $x_0 = -3$ | $x_0 = -2$ | $x_0 = -1$ | $x_0 = 0$ | $x_0 = 1$ | $x_0 = 2$ | $x_0 = 3$ |
| :------------: | :--------: | :--------: | :--------: | :-------: | :-------: | :-------: | :-------: |
| $y_0 = 2$ | $-4$ | $-3$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y_0 = 1$ | $-3$ | $-2 | $-1$ | $0$ | $1$ | $2$ | $3$ |
| $y_0 = 0$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | $3$ | $4$ |
| $y_0 = -1$ | $-1$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ |
| $y_0 = -2$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ |
#### Euler-Schritte
Ein Weg, um eine Lösung für eine Differentialgleichung zu approximieren ist die Methode der Euler-Schritte.
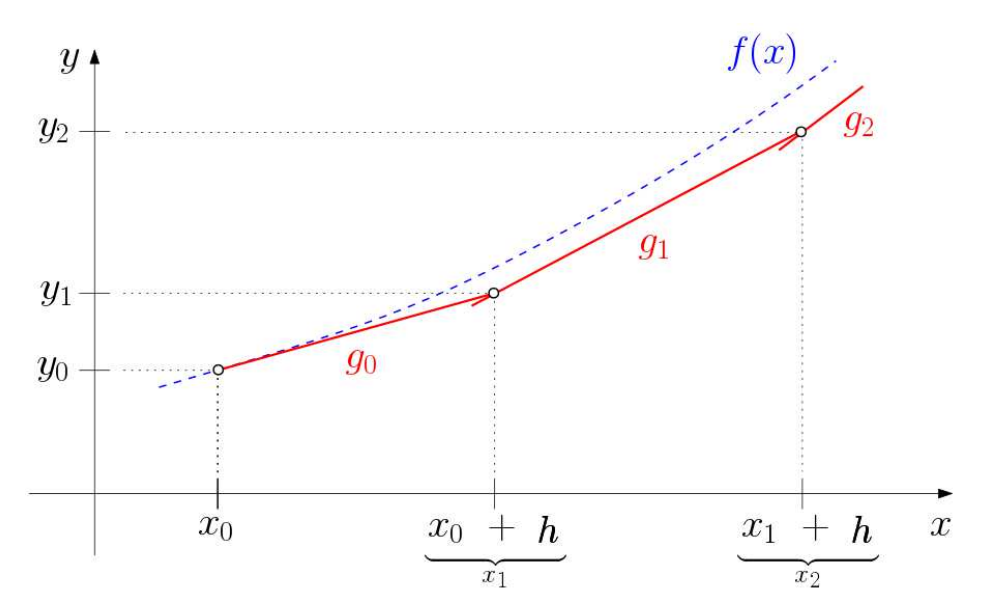
Beispiel mit folgenden Parametern:
$y' = x + y, x_0 = 0, y_0 = 1, h = 1$
| Steigung Gerade | Berechnung | Beispiel |
| -------------------------------------------- | --------------------------------- | ---------------------------- |
| $g_0\text{: } m_0 = F(x_0, y_0) = x_0 + y_0$ | $x_1 = x_0 + h$ | $= 0 + 1 = 1$ |
| Im Beispiel: $1$ | $y_1 = y_0 + h \cdot F(x_0, y_0)$ | $= 1 + 1 \cdot (0 + 1) = 2$ |
| $g_1\text{: } m_1 = F(x_1, y_1) = x_1 + y_1$ | $x_1 = x_0 + h$ | $= 1 + 1 = 2$ |
| Im Beispiel: $3$ | $y_1 = y_0 + h \cdot F(x_1, y_1)$ | $= 2 + 1 \cdot (1 + 2) = 5$ |
| $g_2\text{: } m_2 = F(x_2, y_2) = x_2 + y_2$ | $x_3 = x_2 + h$ | $= 2 + 1 = 3$ |
| Im Beispiel: $7$ | $y_3 = y_2 + h \cdot F(x_2, y_2)$ | $= 5 + 1 \cdot (2 + 5) = 12$ |
| etc. | etc. | etc. |
Den Abstand zwischen den einzelnen Euler-Schritte $h$ kann hierbei frei gewählt werden. Je kleiner $h$ gewählt wird, desto genauer wird das Resultat.
### Separierbare Differentialgleichungen
#### Definition
Eine Differentialgleichung 1. Ordnung ist _separierbar-, wenn sie sich in folgende Form bringen lässt:
$$y' = f(x) \cdot g(y)$$
> #### Beispiele
> - $y' = (x^2 + \sin(x)) \cdot (e^y - y + 7)$ ist separierbar
> - $y' = x - y + 1$ ist _nicht_ separierbar
#### Lösungsweg
1. Gleichung zu Differentialquotient umschreiben:
$y' = \frac{dy}{dx} = f(x) \cdot g(y)$
2. Trennung der Variablen:
$\frac{dy}{g(y)} = f(x) \cdot dx$
3. Integration auf beiden Seiten der Gleichung:
$\int{\frac{dy}{g(y)} = \int{f(x) \cdot dx}}$
4. Auflösen nach $y$
#### Beispiel
$$y' = k \cdot y$$
**1. Gleichung zu Differentialquotient umschreiben:**
$$y' = \frac{dy}{dx} = \underbrace{k}_{f(x)} \cdot \underbrace{y}_{g(y)}$$
**2. Trennung der Variablen:**
Alle $x$ und $y$ auf separate Seite des $=$ bringen:
$$\frac{dy}{y} = k \cdot dx$$
**3. Integration auf beiden Seiten der Gleichung:**
$$\int{\frac{dy}{y}} = \int{\frac{1}{y}}dy = \ln(|y|) \\
\int{k \cdot dx} = k \cdot x + C \\
\ln(|y|) = k \cdot x + C$$
**4. Auflösen nach $y$:**
$$\ln(|y|) = k \cdot x + C \\
|y| = e^{k \cdot x + C} \\
y = \pm e^{k \cdot x + C} = \underbrace{\pm e^C}_{a} \cdot e^{k \cdot x} = a \cdot e^{k \cdot x}$$
**Kontrolle:**
$$y' = (a \cdot e^{k \cdot x})' = a \cdot k \cdot e^{k \cdot x} \\
k \cdot y = k \cdot a \cdot e^{k \cdot x} \\
y' = k \cdot y$$
### Autonome Differentialgleichung
Als autonom werden die Differentialgleichungen bezeichnet, die sich in folgende Form bringen lassen:
$$y' = f(y)$$
#### Beispiele
| Gleichung | Autonom? |
| -------------------------------------------- | -------- |
| $y' = y^2 + 6$ | Ja |
| $y' = x + y$ | Nein |
| $y' = \frac{y}{x}$ | Nein |
| $y' = y^2 \cdot \sqrt{1 - \sin(y)} - \ln(y)$ | Ja |
#### Lösungsweg
Gleich wie [separierbare Differentialgleichungen](#separierbare-differentialgleichungen).
### Lineare Differentialgleichung 1. Ordnung
Eine Differentialgleichung 1. Ordnung ist _lineare_, wenn sie sich in folgende Form bringen lässt:
$$y' = f(x) \cdot y + g(x)$$
$g(x)$ wird hierbei als _Störglied_ oder _Störfunktion_ bezeichnet.
Solche Differentialgleichungen nennen sich _"linear"_, weil sowohl $y$ als auch $y'$ keinen Exponenten haben. Es spielt es keine Rolle, ob $x$ in $f(x)$ oder $g(x)$ eine Potenz hat.
Eine lineare Differentialgleichung 1. Ordnung ist dann _homogen_, wenn $g(x)$ $0$ entspricht. In allen anderen Fällen ist die Differentialgleichung _inhomogen_.
#### Lösungswege
##### Lösung durch Variabel-Separierung
Beispiel anhand folgender Formel:
$$y' = \frac{2y}{x} + x^3$$
**1. Komponenten der linearen Differentialgleichung bestimmen:**
$$\begin{align*}
f(x) &= \frac{2}{x} \\
g(x) &= x^3
\end{align*}$$
**2. Homogenen Anteil berechnen:**
In diesem Schritt wird die Differentialgleichung ***ohne $g(x)$*** berechnet.
Dies funktioniert mit Hilfe der Variabel-Trennung nach folgender Formel:
$$y_h = C \cdot e^{\int{f(x)}dx}$$
Für das Beispiel ergibt das folgendes:
$$y_h = C \cdot e^{\int{\frac{2}{x}}} = C \cdot e^{2 \cdot \ln(|x|)} = C \cdot e^{\ln(|x|^2)} = C \cdot e^{\ln(x^2)} = C \cdot x^2$$
**3. Partikulären Anteil berechnen:**
Mit Hilfe der folgenden Formel kann der Partikuläre Anteil berechnet werden:
$$y_P = y_h \cdot \int{\frac{g(x)}{y_h}}dx$$
Für das Beispiel ergibt das wiederum:
$$y_P = C \cdot x^2 \cdot \int{\frac{x^3}{C \cdot x^2}}dx = x^2 \cdot \int{x} = x^2 \cdot \frac{x^2}{2} = \frac{x^4}{2}$$
**4. Homogenen und Partikulären Anteil addieren:**
$$y = y_h + y_P = C \cdot x^2 + \frac{x^4}{2}$$
##### Lösung durch Variation der Konstanten
Eine weitere Möglichkeit ist das Verfahren "Variation der Konstanten".
Folgend ein Beispiel anhand folgender Differentialgleichung:
$$y' = \cos(x) - \frac{y}{x}\text{ für x > 0}$$
**1. Komponenten bestimmen:**
$$\begin{align*}
f(x) &= -\frac{1}{x} \\
g(x) &= \cos(x) \\
F(x) &= -\ln(x)\text{ für x > 0}
\end{align*}$$
**2. Homogene Gleichung berechnen:**
Mit Hilfe folgender Formel lässt sich der homogene Anteil berechnen:
$$y_0 = C \cdot e^{F(x)}$$
Im aktuellen Beispiel ergibt das folgendes:
$$y_0 = C \cdot e^{F(x)} = C \cdot e^{-\ln(x)} = \frac{C}{x}$$
**3. Konstante $C$ ersetzen**
Im nächsten Schritt wird die Konstante $C$ im zuvor berechneten homogenen Anteil durch folgende Formel ersetzt:
$$K(x) = \int{g(x) \cdot e^{-F(x)}}dx$$
Für das Beispiel ergibt das folgendes:
$$\begin{align*}
\frac{K(x)}{x} \\
&= \frac{1}{x} \cdot \int{g(x) \cdot e^{-F(x)}}dx \\
&= \frac{1}{x} \cdot \int{\cos(x) \cdot e^{\ln(x)}}dx \\
&= \frac{1}{x} \cdot \int{\cos(x) \cdot x}dx \\
&= \frac{1}{x} \cdot (\sin(x) \cdot x + \cos(x)) \\
&= \frac{\sin(x) \cdot x + \cos(x)}{x}
\end{align*}$$
## Anwendung der Integralrechnung
### Der Mittelwert
Der Mittelwert einer Funktion errechnet sich mit der folgenden Formel:
$$\mu = \frac{1}{b - a} \cdot \int_a^b{f(x)}dx$$
### Die Arbeit
$$\int_{s_1}^{s_2}{F(s)}ds$$
### Rotationskörper
#### Rotationskörper um die $x$-Achse
$$V = \pi \cdot \int_a^b{(f(x))^2}dx$$
#### Rotationskörper um die $y$-Achse
$$V = \pi \cdot \int_c^d{(g(y))^2}dy$$
#### Mantelfläche eines Rotationskörpers
$$M = 2 \cdot \pi \cdot \int_a^b{y \cdot \sqrt{1 + (y')^2}}dx$$
### Bogenlänge einer Kurve
$$s = \int_a^b{\sqrt{1 + (y')^2}}dx$$
### Schwerpunkt
$$x_S = \frac{1}{A} \cdot \int_a^b{x \cdot (f_o(x) - f_u(x))}dx$$
$$y_S = \frac{1}{2A} \cdot \int_a^b{(f_o^2(x) - f_u^2(x))}dx$$
### Schwerpunkt eines Rotationskörpers
$$x_S = \frac{\pi}{V} \cdot \int_a^b{x \cdot f^2(x)}dx$$
$$y_S = 0$$
$$z_S = 0$$
## Taylor-Reihen
### Herleitung
#### Polynom durch Stützpunkte Legen
Um ein Polynom auf $n$ Stützpunkte zu legen, muss das Polynom vom Grad $n - 1$ sein.
Mit Hilfe eines Gleichungssystems lässt sich bestimmen, durch welche bestimmte Stützpunkte durchquert.
##### Beispiel
Der Vorgang wird anhand der Gleichung $f(x) = e^{2x}$ aufgezeigt.
**1. Stützpunkte Identifizieren:**
Der Graph $f(x) = e^{2x}$ läuft unter anderem durch die folgenden Stellen:
- $(0, 1)$
- $(1, e^2)$
- $(2, e^4)$
**2. Gleichungssystem aufstellen:**
Für 3 Stützpunkte benötigt das Polynom, wie erwähnt, einen Grad von $3$.
Ein Polynom 3. Grades hat den folgenden Aufbau:
$$p(x) = a + bx + cx^2$$
Daraus lässt sich anhand der Stützpunkte folgendes Gleichungssystem aufstellen:
$$\begin{align*}
1 &= a + 0b + 0c \\
e^2 &= a + b + c \\
e^4 &= a + 2b + 4c \\
\end{align*}$$
Das Lösen dieses Gleichungssystems ergibt folgendes:
$$\begin{align*}
a &= 1 \\
b &= e^2 - 1 - c = -14.02 \\
c &= \frac{e^4 + 1}{2} - e^2 = 20.41
\end{align*}$$
Die ergebende Polynomfunktion ist:
$$p(x) = 1 - 14.02x + 20.41x^2$$
#### Lokale Approximation
Ziel der lokalen Approximation ist es, eine Annäherung an eine Funktion zu finden, die an einem bestimmten Punkt $x_0$ besonders genau am Funktionswert $f(x_0)$ liegt.
Dies ist möglich mit der folgenden Formel:
##### Taylor-Polynom
Für eine Approximation mit einem _Taylor-Polynom_ vom Grad $n$ der Funktion $f(x)$ an der Stelle $x_0$ kann folgende Formel verwendet werden:
$$p(x) = \sum_{k = 0}^{n}{\frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k}$$
##### Taylor-Reihe
Unter _Taylor-Reihe_ versteht man ein unendliches Taylor-Polynom:
$$t_f(x) = \sum_{k = 0}^\infin{\frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k}$$
### Konvergenz
Die Konvergenz beschreibt den Fakt, dass Annäherungen zum Teil mit der anzunähernden Funktion übereinstimmen.
Hierbei steht der Konvergenz-Bereich für die Stellen, an denen die Funktion und die Annäherung übereinstimmen.
#### Potenzreihen
Grundsätzliche Formel einer Potenzreihe.
$$P(x) = \sum_{k = 0}^\infin{a_k \cdot (x - x_0)^k}$$
> **Quotienten-Kriterium:**
> Für _jede_ Potenzreihe $P(x) = \sum_{k = 0}^\infin{a_k \cdot (x - x_0)^x}$ gibt es einen Abstand $r$, so dass
> * alle $x \in (x_0 - r, x_0 + r)$ zum Konvergenz-Bereich gehören
> * alle $x \in (-\infin, x_0 - r) \cup (x_0 + r, \infin)$ nicht zum Konvergenz-Bereich gehören
https://tu-freiberg.de/sites/default/files/media/fakultaet-fuer-mathematik-und-informatik-fakultaet-1-9277/lorz/grundintegrale.pdf
[^Derivation]: [Ableitungen][Derivation]
[Derivation]: ../.../../../Semester%201/AN1%20-%20Analysis%201/Ableitungen.md