Add pre-existing notes
209
Notes/Semester 1/AN1 - Analysis 1/Ableitungen.md
Normal file
|
|
@ -0,0 +1,209 @@
|
|||
<script src="../../../assets/deployggb.js"></script>
|
||||
<script src="../../../assets/graphs.js"></script>
|
||||
<script>
|
||||
window.graphs(
|
||||
[
|
||||
[
|
||||
"example",
|
||||
[
|
||||
"f(x) = (x^4 - 1)^2",
|
||||
"f'(x)"
|
||||
]
|
||||
],
|
||||
[
|
||||
"distance-time",
|
||||
[
|
||||
"t(x) = sqrt(x)",
|
||||
"t'"
|
||||
],
|
||||
(api) =>
|
||||
{
|
||||
api.setAxisUnits(1, "h", "km");
|
||||
}
|
||||
],
|
||||
[
|
||||
"detect",
|
||||
[
|
||||
"f(x) = (x + 1)(x - 1)(x - 2)",
|
||||
"f'",
|
||||
"ComplexRoot(f')",
|
||||
"Extremum(f)",
|
||||
"s_1 = Line(A, z_2)",
|
||||
"s_2 = Line(B, z_1)"
|
||||
],
|
||||
(api) =>
|
||||
{
|
||||
api.setColor("s_1", 0, 128, 0);
|
||||
api.setColor("s_2", 0, 128, 0);
|
||||
api.setLineStyle("s_1", 1);
|
||||
api.setLineStyle("s_2", 1);
|
||||
}
|
||||
]
|
||||
]);
|
||||
</script>
|
||||
|
||||
# Ableitungen
|
||||
Die Ableitung einer Funktion sagt aus, wie sich die Werte der Funktion an einer gegebenen Stelle verändern.
|
||||
|
||||
<div id="example"></div>
|
||||
|
||||
Wie zu sehen ist, zeigt $f'(x)$ an Stellen, an denen $f(x)$ eine Steigung hat, einen positiven Wert, an Stellen, an denen $f(x)$ keine Steigung hat, $0$ und an Stellen, an denen $f(x)$ sich senkt, einen negativen Wert.
|
||||
|
||||
Ableitungen werden jeweils als den Funktions-Namen zusammen mit einem Apostroph geschrieben. So heisst also beispielsweise die Ableitung der Funktion $z(x)$ üblicherweise $z'(x)$.
|
||||
|
||||
> **_Note:_**
|
||||
> Will man die Ableitung eines Terms ausdrücken, so macht man das folgendermassen:
|
||||
>
|
||||
> Die Ableitung von $420x - 1337x^2$ ist $(420x - 1337x^2)'$.
|
||||
|
||||
## Inhaltsverzeichnis
|
||||
- [Ableitungen](#ableitungen)
|
||||
- [Inhaltsverzeichnis](#inhaltsverzeichnis)
|
||||
- [Realbeispiel](#realbeispiel)
|
||||
- [Ableitungen erkennen](#ableitungen-erkennen)
|
||||
- [Zweite, Dritte, $n$. Ableitung](#zweite-dritte-n-ableitung)
|
||||
- [Ableitungs-Regeln](#ableitungs-regeln)
|
||||
- [Allgemeine Regeln](#allgemeine-regeln)
|
||||
- [Konstante](#konstante)
|
||||
- [Faktor-Regel](#faktor-regel)
|
||||
- [Potenz-Regel](#potenz-regel)
|
||||
- [Summen-Regel](#summen-regel)
|
||||
- [Produkt-Regel](#produkt-regel)
|
||||
- [Quotienten-Regel](#quotienten-regel)
|
||||
- [Ketten-Regel](#ketten-regel)
|
||||
- [Ableitungen bestimmter Funktionen](#ableitungen-bestimmter-funktionen)
|
||||
|
||||
## Realbeispiel
|
||||
Die Ableitung kann beispielsweise verwendet werden, um die Geschwindigkeit einer Bewegung abzubilden.
|
||||
|
||||
Folgendes Weg-Zeit-Diagramm soll das verdeutlichen:
|
||||
|
||||
<div id="distance-time"></div>
|
||||
|
||||
Nicht nur zeigt hier $t'$ die Ableitung der Funktion $t$ auf, sondern auch jeweils die momentane Geschwindigkeit, die eine Person zum gegebenen Zeitpunkt hat.
|
||||
|
||||
## Ableitungen erkennen
|
||||
Ableitungen kann man daran erkennen, dass sie jeweils an den Stellen, an denen die abzuleitende Funktion einen Scheitelpunkt erreicht, einen Wert von $0$ haben, da an diesen Stellen weder eine Senkung noch eine Steigung vorherrscht.
|
||||
|
||||
Beispiel:
|
||||
|
||||
<div id="detect"></div>
|
||||
|
||||
## Zweite, Dritte, $n$. Ableitung
|
||||
Erstellt man eine Ableitung einer bereits existierenden Ableitung, so nennt sich diese "Zweite Ableitung". Dessen Ableitung wiederum heisst "Dritte Ableitung" etc.
|
||||
|
||||
> **_In Worten:_**
|
||||
> - $f'$ ist die Ableitung von $f$
|
||||
> - $f''$ ist die Ableitung von $f'$ und somit die **Zweite Ableitung** von $f$
|
||||
> - $f'''$ ist die Ableitung von $f''$ und somit die **Dritte Ableitung** von $f$
|
||||
|
||||
## Ableitungs-Regeln
|
||||
Um von einer Funktion (oder Bruchteilen davon) die Ableitung zu errechnen, können einige allgemeingültige Regeln zugezogen werden, welche im Folgenden erklärt werden.
|
||||
|
||||
Hilfreiche Links für's Nachschlagen der Regeln:
|
||||
- https://www.mathebibel.de/ableitungsregeln
|
||||
- https://www.youtube.com/watch?v=GtVWdeevZpw
|
||||
|
||||
### Allgemeine Regeln
|
||||
#### Konstante
|
||||
Besteht in der Funktion nur eine Konstante ohne ein $x$, so ist dessen Ableitung immer $0$:
|
||||
|
||||
| Funktion | Ableitung |
|
||||
| ----------------- | ----------- |
|
||||
| $f(x) = 1337$ | $f'(x) = 0$ |
|
||||
| $f(x) = \sqrt{2}$ | $f'(x) = 0$ |
|
||||
|
||||
#### Faktor-Regel
|
||||
Die Faktor-Regel besagt, dass konstante Zahlen, mit denen $x$ multipliziert werden, auch in dessen Ableitung bestehen bleiben.
|
||||
|
||||
> $$f(x) = c \cdot x \rightarrow f'(x) = c \cdot (x)'$$
|
||||
|
||||
Das bedeutet folgendes:
|
||||
|
||||
Wenn $f(x)$ folgender Funktion entspricht:
|
||||
|
||||
$f(x) = 2 \cdot g(x)$ und $g(x) = x$
|
||||
|
||||
So ist die Ableitung davon folgende:
|
||||
$$f(x) = 2 \cdot g'(x)$$
|
||||
|
||||
| Funktion | Ableitung |
|
||||
| ----------- | --------- |
|
||||
| $f(x) = 7x$ | $7$ |
|
||||
|
||||
#### Potenz-Regel
|
||||
Die Potenzregel lautet folgendermassen:
|
||||
|
||||
> $$f(x) = x^n \rightarrow f'(x) = n \cdot x^{n - 1}$$
|
||||
|
||||
Auch hier wieder anhand einiger Beispiele:
|
||||
|
||||
| Funktion | Ableitung |
|
||||
| ------------- | ----------------------- |
|
||||
| $f(x) = x$ | $1$ |
|
||||
| $f(x) = x^7$ | $7 \cdot x^6$ |
|
||||
| $f(x) = x^6$ | $6 \cdot x^5$ |
|
||||
| $f(x) = 3x^6$ | $3 \cdot (6 \cdot x^5)$ |
|
||||
|
||||
#### Summen-Regel
|
||||
Die Ableitung einer Addition ergibt die Summe der Ableitung der einzelnen Summanden der Addition:
|
||||
|
||||
> $$f(x) = g(x) + h(x) \rightarrow f'(x) = g'(x) + h'(x)$$
|
||||
|
||||
Diese Regel ist auch auf Subtraktionen anwendbar:
|
||||
|
||||
> $$f(x) = g(x) - h(x) \rightarrow f'(x) = g'(x) - h'(x)$$
|
||||
|
||||
Diese Regel kann für jegliche Funktion, welche eine Addition beinhaltet, angewendet werden:
|
||||
|
||||
$$f(x) = \overbrace{2x}^{g(x) = 2x} + \overbrace{4x^3}^{h(x) = 4x^3}$$
|
||||
$$f'(x) = g'(x) + h'(x)$$
|
||||
$$f'(x) = \underbrace{2 \cdot 1 \cdot x^0}_{g'(x) = 2 \cdot 1 \cdot x^0} + \underbrace{4 \cdot 3 \cdot x^2}_{h'(x) = 4 \cdot 3 \cdot x^2}$$
|
||||
|
||||
#### Produkt-Regel
|
||||
Die Produkt-Regel beschreibt, wie eine Ableitung einer Funktion gemacht werden kann, welche eine Multiplikation beinhaltet.
|
||||
|
||||
> $$f(x) = g(x) \cdot h(x) \rightarrow f'(x) = g'(x) \cdot h(x) + g(x) \cdot h'(x)$$
|
||||
|
||||
Auch hier wiederum ein Beispiel:
|
||||
$$f(x) = \overbrace{(3x^3 + x^2)}^{g(x) = 3x^3 + x^2}\overbrace{(4x^2 + 1)}^{h(x) = 4x^2 + 1}$$
|
||||
$$f'(x) = g'(x) \cdot h'(x)$$
|
||||
$$f'(x) = \underbrace{(3 \cdot 3 x^2 + 1 \cdot x^1)}_{g'(x) = 3 \cdot 3 x^2 + 1 \cdot x^1} \cdot \overbrace{(4x^2 + 1)}^{h(x)} + \overbrace{(3x^3 + x^2)}^{g(x)} \cdot \underbrace{(4 \cdot 2 \cdot x^1 + 0)}_{h'(x) = 4 \cdot 2 \cdot x^1 + 0}$$
|
||||
|
||||
#### Quotienten-Regel
|
||||
Von der Produkt-Regel lässt sich auch die Quotienten-Regel ableiten. Diese beschreibt, wie man die Ableitung von Divisionen bilden kann und lautet folgendermassen:
|
||||
|
||||
> $$f(x) = \frac{g(x)}{h(x)} \rightarrow \frac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{(h(x))^2}$$
|
||||
|
||||
Wie diese Regel angewendet wird, lässt sich anhand des folgenden Beispiels aufzeigen:
|
||||
|
||||
$$f(x) = \left(\frac{\overbrace{3x^2 - x}^{g(x)}}{\underbrace{2x^3 + 1}_{h(x)}}\right)$$
|
||||
$$f'(x) = \frac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{(h(x))^2}$$
|
||||
$$f'(x) = \frac{\overbrace{(3 \cdot 2 \cdot x^1 - 1 \cdot x^0)}^{g'(x)} \cdot \overbrace{(2x^3 + 1)}^{h(x)} - \overbrace{(3x^2 - x)}^{g(x)} \cdot \overbrace{(2 \cdot 3 \cdot x^2 + 0)}^{h'(x)}}{(\underbrace{2x^3 + 1}_{h(x)})^2}$$
|
||||
|
||||
#### Ketten-Regel
|
||||
Die Ketten-Regel zeigt auf, wie die Ableitung von verschachtelten Funktionen geformt werden kann.
|
||||
|
||||
Folgende Regel gilt:
|
||||
|
||||
> $$f(x) = g(h(x)) \rightarrow f'(x) = g'(h(x)) \cdot h'(x)$$
|
||||
|
||||
Aufgezeigt anhand eines Beispiels:
|
||||
|
||||
$$f(x) = \overbrace{(\underbrace{x^3 + 4}_{h(x) = x^3 + 4})^{-2}}^{g(x) = x^{-2}}$$
|
||||
$$f'(x) = g'(h(x)) \cdot h'(x)$$
|
||||
$$f'(x) = \overbrace{-2 \cdot (\underbrace{x^3 + 4}_{h(x)})^{-3}}^{g'(h(x))} \cdot \overbrace{(3 \cdot x^2 + 0)}^{h'(x)}$$
|
||||
|
||||
### Ableitungen bestimmter Funktionen
|
||||
Folgende Auflistung zeigt einige bekannte Funktionen und deren Ableitung auf.
|
||||
|
||||
$a$ steht hierbei für eine Konstante.
|
||||
|
||||
| Ausdruck | Ableitung |
|
||||
| -------------- | -------------------------- |
|
||||
| $(\sin(x))'$ | $\cos(x)$ |
|
||||
| $(\cos(x))'$ | $-\sin(x)$ |
|
||||
| $(e^x)'$ | $e^x$ |
|
||||
| $(a^x)'$ | $a^x \cdot \ln(a)$ |
|
||||
| $(\ln(x))'$ | $\frac{1}{x}$ |
|
||||
| $(\log_a(x))'$ | $\frac{1}{x \cdot \ln(a)}$ |
|
||||
BIN
Notes/Semester 1/AN1 - Analysis 1/Convention.png
Normal file
|
After 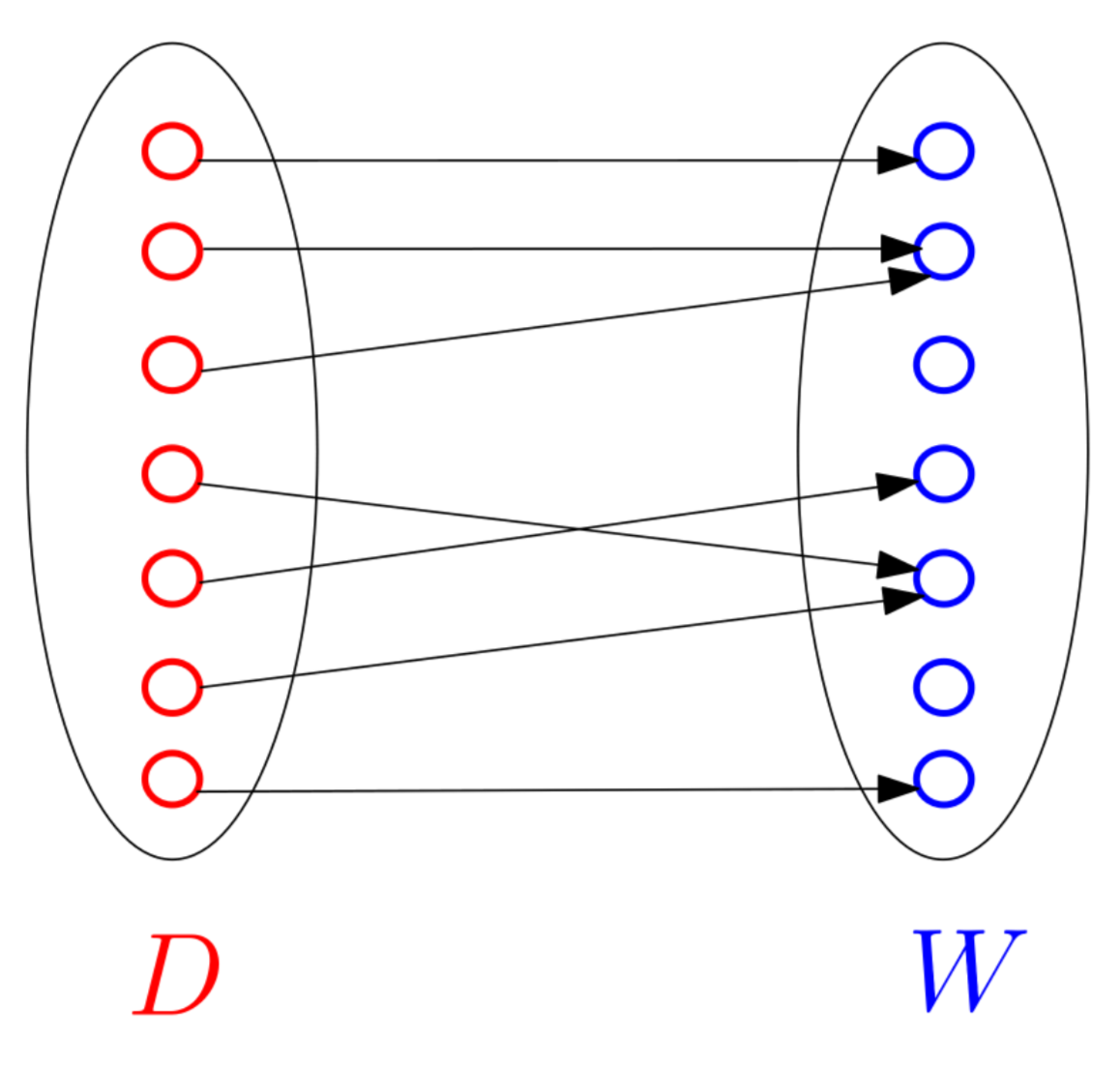
(image error) Size: 185 KiB |
35
Notes/Semester 1/AN1 - Analysis 1/Formale Notation.md
Normal file
|
|
@ -0,0 +1,35 @@
|
|||
# Formale Notation
|
||||
## Mengen
|
||||
### Reelle Zahlen
|
||||
$\mathbb{R}$
|
||||
|
||||
### Ohne
|
||||
$\mathbb{R} \setminus 1$
|
||||
|
||||
> ***Note:***
|
||||
> Gesprochen: "Alle reellen Zahlen ($\mathbb{R}$) ohne 1."
|
||||
|
||||
$\mathbb{D} = [0, \infty[$ (gesprochen: "Alle Zahlen ab 0 ohne $\infty$)
|
||||
|
||||
### Fakultät
|
||||
Die Fakultät errechnet sich, indem man die Werte aller Zahlen in einer Zahlenwerte summiert.
|
||||
|
||||
So berechnet sich die Fakultät von $100$ bspw. indem man folgendes rechnet:
|
||||
$$1 + 2 + 3 + 4 + 5 + 6 +...+100$$
|
||||
|
||||
Bildet man jedoch die Zahlenreihe zweimal in entgegengesetzter Richtung, wird möglicherweise auffallen, dass sich jeweils Zahlenpaare bilden, die immer die Summe der äussersten Zahlen der Reihe zusammenrechnet:
|
||||
|
||||
$$\underbrace{1}_{100} + \underbrace{2}_{99} + \underbrace{3}_{98} ... + \underbrace{100}_{1}$$
|
||||
|
||||
Alle Zahlenpaare zusammen ergeben $100 \times 101$.
|
||||
|
||||
Da in dieser Zusammenfassung jedes Zahlenpaar doppelt vorkommt, muss die Lösung dieser Rechnung halbiert werden, um die Lösung der Fakultät zu erhalten:
|
||||
|
||||
$$\sum^{100}_{k=1}k = \frac{100 \times (100 + 1)}{2} = 5050$$
|
||||
|
||||
Dementsprechend kann auch die Fakultät anderer Zahlen errechnet werden:
|
||||
|
||||
$$\sum^{n}_{k=1}k = \frac{n \times (n + 1)}{2}$$
|
||||
|
||||
#### Quadrat Gagg
|
||||
$$\sum^{n}_{k=1}k^2 = \frac{n \cdot (n + 1) \cdot (2n + 1)}{6}$$
|
||||
18
Notes/Semester 1/AN1 - Analysis 1/Funktionen.md
Normal file
|
|
@ -0,0 +1,18 @@
|
|||
<script src="../../assets/deployggb.js"></script>
|
||||
<script src="../../assets/graphs.js"></script>
|
||||
<script>
|
||||
window.graphs(
|
||||
[
|
||||
|
||||
]);
|
||||
</script>
|
||||
|
||||
# Funktionen
|
||||
Funktionen bilden Vorschriften, Vorgänge oder Berechnungen ab, in denen jeweils die Werte eines Definitionsbereichs $\mathbb{D}$ je genau einem Ausgabewert aus dem Wertbereich $\mathbb{W}$ zugeordnet werden.
|
||||
|
||||
Sowohl Definitions- als auch Wertebereich entsprechen, falls nicht angegeben, jeweils den reellen Zahlen $\mathbb{R}$
|
||||
|
||||

|
||||
|
||||
|
||||
$env:Path -split ';'
|
||||
1
Notes/Semester 1/AN1 - Analysis 1/Polynome.md
Normal file
|
|
@ -0,0 +1 @@
|
|||
# Polynome
|
||||
4
Notes/Semester 1/AN1 - Analysis 1/Table of Contents.md
Normal file
|
|
@ -0,0 +1,4 @@
|
|||
# Inhaltsverzeichnis
|
||||
- [Formale Notation](./Formale%20Notation.md)
|
||||
- [Polynome](./Polynome.md)
|
||||
- [Ableitungen](./Ableitungen.md)
|
||||
20
Notes/Semester 1/DB - Datenbanken/Daten-Arten.md
Normal file
|
|
@ -0,0 +1,20 @@
|
|||
# Daten-Arten
|
||||
Der grundsätzliche Unterschied zwischen Objekt- und Daten-Notationen (wie bspw. `JSON`, `XML`, `CSV` und `XLSX`) und herkömmlichen Datenbanken ist, dass genannte Notationen `Semi-Strukturiert` und die Daten in der Datenbank sind `Vollständig Strukturiert`.
|
||||
|
||||
In den genannten Notationen können falsche Daten angegeben werden können (obwohl sie falsch sind, können sie gespeichert werden, da genannte Dateien üblicherweise als freitext bearbeitbar sind). In strukturierten Datenbanken können nur - gemäss Vorgaben - vollständige Daten abgespeichert werden.
|
||||
|
||||
## Datenverwaltung mittels Dateisystem
|
||||
Zwar nutzen auch Datenbanken
|
||||
|
||||
```mermaid
|
||||
graph TD;
|
||||
app1[Anwendungs-Programm 1];
|
||||
appN[Anwendungs-Programm n];
|
||||
dbms["Datenbank Management System (DMBS)"];
|
||||
base[Datenbank Datenbasis];
|
||||
app1 --> dbms;
|
||||
dbms --> app1;
|
||||
appN --> dbms;
|
||||
dbms --> appN;
|
||||
dbms --> base;
|
||||
```
|
||||
5
Notes/Semester 1/DB - Datenbanken/Korrektes ERD.md
Normal file
|
|
@ -0,0 +1,5 @@
|
|||
# Korrektes ERD
|
||||
1. ERD mit einem leeren Blatt beginnen
|
||||
2. Definiere die unabhängigen Entitäts-Typen (Tabelle, welche keine Fremdschlüssel besitzen)
|
||||
3. Definiere die Referenz-Typen
|
||||
4. Attribute zu nun vorhandenen Entitäts-Typen hinzufügen
|
||||
94
Notes/Semester 1/DB - Datenbanken/Relationale Algebra.md
Normal file
|
|
@ -0,0 +1,94 @@
|
|||
# Relationale Algebra
|
||||
Die Rechen-Operationen, die vom Datenbank-Server ausgeführt werden, um Datensätze abzufragen, heisst Relationale Algebra.
|
||||
Relationale Algebra ist im Prinzip die Computer-Sprache, zu der SQL-Abfragen vor der Ausführung umgewandelt werden.
|
||||
|
||||
## Operation Vereinigung $\cup$
|
||||
Vereinigt zwei Relationen und entfernt alle Duplikate.
|
||||
|
||||

|
||||
|
||||
**_Beispiel:_**
|
||||
**ActionActors:**
|
||||
| FirstName | LastName | YearOfBirth |
|
||||
| --------- | -------- | ----------- |
|
||||
| Jackie | Chan | 1954 |
|
||||
| Jason | Statham | 1967 |
|
||||
| Vin | Diesel | 1967 |
|
||||
|
||||
**ComedyActors:**
|
||||
| FirstName | LastName | YearOfBirth |
|
||||
| --------- | -------- | ----------- |
|
||||
| Jackie | Chan | 1954 |
|
||||
| Ryan | Reynolds | 1976 |
|
||||
| Jack | Black | 1969 |
|
||||
|
||||
**ActionActors $\cup$ ComedyActors:**
|
||||
| FirstName | LastName | YearOfBirth |
|
||||
| --------- | -------- | ----------- |
|
||||
| Jackie | Chan | 1954 |
|
||||
| Jason | Statham | 1967 |
|
||||
| Vin | Diesel | 1967 |
|
||||
| Ryan | Reynolds | 1976 |
|
||||
| Jack | Black | 1969 |
|
||||
|
||||
> **_In Worten:_**
|
||||
> Alle Schauspieler, die in Action- oder in Comedy-Filmen spielen.
|
||||
|
||||
|
||||
## Operation Intersection $\cap$
|
||||
Alle Elemente, die in beiden Relationen vorkommen.
|
||||
|
||||

|
||||
|
||||
**_Beispiel:_**
|
||||
**ActionActors:**
|
||||
| FirstName | LastName | YearOfBirth |
|
||||
| --------- | -------- | ----------- |
|
||||
| Jackie | Chan | 1954 |
|
||||
| Jason | Statham | 1967 |
|
||||
| Vin | Diesel | 1967 |
|
||||
|
||||
**ComedyActors:**
|
||||
| FirstName | LastName | YearOfBirth |
|
||||
| --------- | -------- | ----------- |
|
||||
| Jackie | Chan | 1954 |
|
||||
| Ryan | Reynolds | 1976 |
|
||||
| Jack | Black | 1969 |
|
||||
|
||||
**ActionActors $\cap$ ComedyActors:**
|
||||
| FirstName | LastName | YearOfBirth |
|
||||
| --------- | -------- | ----------- |
|
||||
| Jackie | Chan | 1954 |
|
||||
|
||||
> **_In Worten:_**
|
||||
> Alle Schauspieler, die in Action- und in Comedy-Filmen spielen.
|
||||
|
||||
## Operator Differenz $\setminus$
|
||||
Alle Elemente, die in der 1. Relation vorkommen und in der 2. Relation nicht vorkommen.
|
||||
|
||||

|
||||
|
||||
**_Beispiel:_**
|
||||
**ActionActors:**
|
||||
| FirstName | LastName | YearOfBirth |
|
||||
| --------- | -------- | ----------- |
|
||||
| Jackie | Chan | 1954 |
|
||||
| Jason | Statham | 1967 |
|
||||
| Vin | Diesel | 1967 |
|
||||
|
||||
**ComedyActors:**
|
||||
| FirstName | LastName | YearOfBirth |
|
||||
| --------- | -------- | ----------- |
|
||||
| Jackie | Chan | 1954 |
|
||||
| Ryan | Reynolds | 1976 |
|
||||
| Jack | Black | 1969 |
|
||||
|
||||
**ActionActors $\setminus$ ComedyActors:**
|
||||
| FirstName | LastName | YearOfBirth |
|
||||
| --------- | -------- | ----------- |
|
||||
| Jason | Statham | 1967 |
|
||||
| Vin | Diesel | 1967 |
|
||||
|
||||
|
||||
> **_In Worten:_**
|
||||
> Alle Schauspieler, die in Action-Filmen, aber in keinen Comedy-Filmen mitspielen.
|
||||
39
Notes/Semester 1/DB - Datenbanken/SQL-Abfragen.md
Normal file
|
|
@ -0,0 +1,39 @@
|
|||
# SQL-Abfragen
|
||||
SQL-Sprachen (Server Query Language) sind Sprachen, die für Abfragen verwendet werden.
|
||||
Die SQL-Sprachen einzelner Datenbank Management Systeme (wie bspw. `MySQL`, `MariaDB`, `Microsoft SQL` (kurz `MSSQL`), `Oracle DB`, `NoSQL` und `MongoDB`) haben jeweils untereinander geringe Unterschiede.
|
||||
|
||||
Einige Grundsätze sind jedoch bei den meisten Abfrage-Sprachen gleich.
|
||||
|
||||
## Abfrage-Sprache
|
||||
### Einfache Abfragen
|
||||
Ein Beispiel eines in Abfrage-Sprache geschriebener Befehl ist folgender:
|
||||
|
||||
```sql
|
||||
SELECT *
|
||||
FROM Subscriptions
|
||||
WHERE MonthlyPrice > 10.50
|
||||
```
|
||||
|
||||
oder
|
||||
|
||||
```sql
|
||||
SELECT FirstName
|
||||
FROM Member
|
||||
WHERE [ROLE] IN ('Admin', 'Owner')
|
||||
```
|
||||
|
||||
Das erste Beispiel bedeutet folgendes:
|
||||
> Zeige alle Informationen über Abonnements an, deren monatlicher Preis über `10.50` ist.
|
||||
|
||||
Das zweite Beispiel bedeutet folgendes:
|
||||
> Zeige den Vornamen aller Mitglieder an, deren Rolle `Administrator` oder `Eigentümer` ist.
|
||||
|
||||
Der erste Teil eines Befehls gibt jeweils an, welche Informationen abgefragt oder berechnet werden sollen. Der zweite Teil gibt an, aus welchen Tabellen die Informationen gezogen werden sollen. Der dritte, optionale Teil gibt an, unter welchen Bedingungen die Informationen ausgegeben werden sollen.
|
||||
|
||||
### Abfrage über mehrere Tabellen
|
||||
|
||||
```sql
|
||||
SELECT s.Name, COUNT(m.ID)
|
||||
FROM Subscription s, Member m
|
||||
WHERE s.MemberID = m.ID
|
||||
```
|
||||
20
Notes/Semester 1/DB - Datenbanken/SQL-Syntax.md
Normal file
|
|
@ -0,0 +1,20 @@
|
|||
# SQL Syntax
|
||||
Generell lassen sich alle SQL-Statements in 3 verschiedene Arten von Abfragen aufteilen.
|
||||
|
||||
## DDL - Data Definition Language
|
||||
Die `Data Definition Language` sind die Arten von Statements, die nicht den Inhalt der Datenbank, sondern deren Struktur definiert und/oder verändert.
|
||||
|
||||
Wichtige Statements sind hierbei
|
||||
- `CREATE` zum Erstellen eines Elements
|
||||
- `ALTER` zum Verändern eines existierenden Elements
|
||||
- `DROP` zum Löschen eines Elements
|
||||
|
||||
### Elemente in `DDL`
|
||||
| Bezeichnung | Beschreibung |
|
||||
| ----------- | --------------------------------------------- |
|
||||
| `DOMAIN` | Definiert einen benutzerdefinierten Datentyp. |
|
||||
| `SCHEMA` | Gängig:
|
||||
|
||||
CREATE erstellt ein Element
|
||||
ALTER ändert ein Element
|
||||
DROP löscht ein Element
|
||||
5
Notes/Semester 1/DB - Datenbanken/Table of Contents.md
Normal file
|
|
@ -0,0 +1,5 @@
|
|||
# Inhaltsverzeichnis
|
||||
- [Relationale Algebra](./Relationale%20Algebra.md)
|
||||
- [SQL-Abfragen](./SQL-Abfragen.md)
|
||||
- [Daten-Arten](./Daten-Arten.md)
|
||||
- [Lektionen](./Lessons)
|
||||
|
|
@ -0,0 +1,475 @@
|
|||
# Grundbegriffe und elementare Logik
|
||||
## Aussagen, Prädikate, Junktoren und Quantoren
|
||||
### Aussage
|
||||
Eine Aussage beschreibt ein bestimmbares Objekt und deren Eigenschaften - diese lassen sich eindeutig bestätigen oder verneinen.
|
||||
|
||||
> **_Beispiel einer wahren Aussage:_**
|
||||
> "Die Zahl $3$ ist eine Primzahl"
|
||||
>
|
||||
> **_Beispiel einer unwahren Aussage:_**
|
||||
> "Die Zahl $4$ ist eine Primzahl"
|
||||
|
||||
#### Elementaraussagen und zusammengesetzte Aussagen
|
||||
Eine spezielle Art von Aussage ist die sogenannte "Elementaraussage". Hierbei handelt es sich um eine Aussage, die nicht weiter aufgeteilt werden kann.
|
||||
|
||||
Alle anderen Aussagen lassen sich weiter aufteilen und sind somit "zusammengesetzte Aussagen".
|
||||
|
||||
> **_Zum Vergleich:_**
|
||||
> - Elementaraussage:
|
||||
> "Eine Woche hat 7 Tage" ist eine Elementaraussage
|
||||
> - Zusammengesetzte Aussage:
|
||||
> "ein Tag hat 24 Stunden **und** eine Woche hat 7 Tage" eine
|
||||
>
|
||||
> Mehr zu zusammengesetzten Aussagen unter [Junktoren](#junktoren)
|
||||
|
||||
### Prädikat
|
||||
Falls das Objekt, über welches eine Aussage getätigt wird, ohne Einschränkungen frei wählbar ist, handelt es sich nicht um eine Aussage, sondern um ein Prädikat.
|
||||
|
||||
Prädikate, welche von einer Variable abhängen nennen sich "Einstelliges Prädikat".
|
||||
|
||||
> **_Beispiele:_**
|
||||
> - $A(x)$ = "Die gegebene Zahl $x$ ist eine Primzahl"
|
||||
> - $A(x) = x < 3$
|
||||
|
||||
Prädikate, welche von zwei Variablen abhängen nennen sich "Zweiteiliges Prädikat".
|
||||
|
||||
> **_Beispiel:_**
|
||||
> $$A(x, y) = x < y$$
|
||||
|
||||
Mit Hilfe von Prädikaten können auch Aussagen erstellt werden:
|
||||
|
||||
> **_Beispiel:_**
|
||||
>
|
||||
> **_Prädikat:_** $A(x) = x > 100$
|
||||
> **_Aussage:_** $A(10) = 10 > 100$
|
||||
>
|
||||
> Hierbei ist $A$ der Name einer Funktion.
|
||||
|
||||
### Junktoren
|
||||
#### Zusammengesetzte Aussagen
|
||||
Zusammengesetzte Aussagen sind Aussagen, die aus Elementaraussagen bestehen, die durch sogenannte [`Junktoren`](#junktoren) verknüpft werden.
|
||||
|
||||
> **_Beispiel:_**
|
||||
> $$A:=\text{"78 ist keine Primzahl"}$$
|
||||
> $$B:=\text{"15 ist keine Primzahl"}$$
|
||||
> $$C:=\text{"78 ist keine Primzahl und 15 ist keine Primzahl"}$$
|
||||
|
||||
$A$ und $B$ sind Elementaraussagen, $C$ ist eine zusammengesetzte Aussage.
|
||||
|
||||
#### 1. Negation
|
||||
Die Negation wird üblicherweise als "nicht" gesprochen. In Formeln wird die Negation mit dem Symbol $\neg$ geschrieben.
|
||||
|
||||
Als Beispiel - $f$ für "falsch" und $w$ für "wahr":
|
||||
|
||||
| $A$ | $\neg A$ |
|
||||
| :---: | :------: |
|
||||
| $f$ | $w$ |
|
||||
| $w$ | $f$ |
|
||||
|
||||
Bzw. mit $0$ für "falsch" und $1$ für "wahr":
|
||||
|
||||
| $A$ | $\neg A$ |
|
||||
| :---: | :------: |
|
||||
| $0$ | $1$ |
|
||||
| $1$ | $0$ |
|
||||
|
||||
> **_Beispiel:_**
|
||||
> $$A:=\text{"Hans studiert an der ZHAW"}$$
|
||||
> $$\neg A:=(\text{"Hans studiert nicht an der ZHAW"})$$
|
||||
> $$\neg A:=\text{"Es trifft nicht zu, dass Hans an der ZHAW studiert"}$$
|
||||
|
||||
#### 2. Konjunktion
|
||||
Die Konjunktion wird als "und" gesprochen und mit dem Zeichen $\wedge$ geschrieben.
|
||||
|
||||
> **_Beispiel:_**
|
||||
> $$A:=\text{"6 ist durch 2 teilbar"}: wahr$$
|
||||
> $$B:=\text{"8 ist durch 5 teilbar"}: falsch$$
|
||||
> $$A \wedge B :=\text{"6 ist durch 2 teilbar und 8 ist durch 5 teilbar"}: falsch$$
|
||||
|
||||
| $A$ | $B$ | $A \wedge B$ |
|
||||
| :---: | :---: | :----------: |
|
||||
| $0$ | $0$ | $0$ |
|
||||
| $0$ | $1$ | $0$ |
|
||||
| $1$ | $0$ | $0$ |
|
||||
| $1$ | $1$ | $1$ |
|
||||
|
||||
> **_Beispiel:_**
|
||||
> Falls A und B wahr sind:
|
||||
> $A$: w
|
||||
> $B$: w
|
||||
>
|
||||
> 1. $A \wedge B$: w
|
||||
> 2. $\neg A \wedge B$: f
|
||||
> 3. $A \wedge \neg B$: f
|
||||
> 4. $\neg A \wedge \neg B$: f
|
||||
|
||||
#### 3. Disjunktion
|
||||
Die Disjunktion wird als "oder" gesprochen und mit dem Zeichen $\vee$ dargestellt.
|
||||
|
||||
**_Beispiel:_**
|
||||
> $$A:=\text{"9 ist durch 3 teilbar"}: wahr$$
|
||||
> $$B:=\text{"9 ist eine Quadratzahl"}: wahr$$
|
||||
> $$A \vee \neg B:=\text{"9 ist durch 3 teilbar oder 9 ist keine Quadratzahl"}: wahr$$
|
||||
|
||||
Ist eine der Aussagen der Disjunktion wahr, so ist auch die Disjunktion wahr.
|
||||
|
||||
| $A$ | $B$ | $A \vee B$ |
|
||||
| :---: | :---: | :--------: |
|
||||
| $0$ | $0$ | $0$ |
|
||||
| $0$ | $1$ | $1$ |
|
||||
| $1$ | $0$ | $1$ |
|
||||
| $1$ | $1$ | $1$ |
|
||||
|
||||
#### 4. Implikation
|
||||
Die Implikation wird als "wenn $A$, dann $B$" ausgesprochen und in Formeln mit dem Zeichen $\Rightarrow$ geschrieben.
|
||||
|
||||
Sollte $A$ nicht zutreffen, ist das Ergebnis immer wahr ($w$ bzw. $1$).
|
||||
|
||||
> **_Beispiel:_**
|
||||
> $$A:=\text{"Es regnet"}$$
|
||||
> $$B:=\text{"Die Wiese ist nass"}$$
|
||||
|
||||
| $A$ | $B$ | $A \Rightarrow B$ |
|
||||
| :---: | :---: | :---------------: |
|
||||
| $0$ | $0$ | $1$ |
|
||||
| $0$ | $1$ | $1$ |
|
||||
| $1$ | $0$ | $0$ |
|
||||
| $1$ | $1$ | $1$ |
|
||||
|
||||
> ***Merksätze:***
|
||||
> - Wenn $A$ wahr ist, muss auch $B$ wahr sein.
|
||||
> - Wenn $A$ falsch ist, kann $B$ wahr oder falsch sein.
|
||||
|
||||
> **_Beispiel 2:_**
|
||||
> $$A:=\text{"Es gibt Einhörner"}: falsch$$
|
||||
> $$B:=\text{"4 ist eine Primzahl"}: falsch$$
|
||||
>
|
||||
> $$C:=\text{"Wenn es Einhörner gibt, ist 4 eine Primzahl"}: wahr$$
|
||||
|
||||
> ***Note:***
|
||||
> "Falls es Einhörner gibt, ist 4 eine Primzahl."
|
||||
> Einhörner existieren nicht und 4 ist keine Primzahl - die Aussage ist also richtig... bis zum Fund des ersten Einhorns zumindest. :unicorn:
|
||||
|
||||
> **_Beispiel 3:_**
|
||||
> $$A:=\text{"Spinat ist grün"}$$
|
||||
> $$B:=\text{"2 ist eine Primzahl"}$$
|
||||
|
||||
> **_Beispiel 4:_**
|
||||
> $$A:=\text{"Alle Fische leben im Ozean"}$$
|
||||
> $$B:=\text{"Forellen leben im Ozean"}$$
|
||||
> $$C:=\text{"Haie leben im Ozean"}$$
|
||||
> $\underbrace{\text{Alle Fische leben im Ozean}}_{A\text{: falsch}} \Rightarrow \underbrace{\text{Haie leben im Ozean}}_{C\text{: wahr}}$: wahr
|
||||
> $\underbrace{\text{Alle Fische leben im Ozean}}_{A\text{: falsch}} \Rightarrow \underbrace{\text{Forellen leben im Ozean}}_{\text{B: falsch}}$: wahr
|
||||
|
||||
> **_Note:_**
|
||||
> _ex falso sequitur quodlibet_ (lateinisch für "aus Falschem folgt Beliebigest"), abgekürzt "e.f.q" oder eindeutiger _contradictione sequitur quodlibet_ (lateinisch für "aus einem Widerspruch folgt Beliebiges), bezeichnet im eigenen Sinn eines der beiden in vielen logischen Systemen gültigen Gesetze:
|
||||
> 1. Aus einem logisch - nicht bloss faktisch - falschen Satz folgt jede beliebige Aussage.
|
||||
> 2. Aus zwei widersprüchlichen Sätzen folgt jede beliebige Aussage.
|
||||
|
||||
#### 5. Äquivalenz
|
||||
Die Äquivalenz wird "ist gleich" ausgesprochen und mit dem Zeichen $\Leftrightarrow$ geschrieben.
|
||||
|
||||
Dieser Junktor beschreibt, dass beide Aussagen äquivalent sind. In diesem Fall gilt:
|
||||
|
||||
$$A \Rightarrow B \wedge B \Rightarrow A$$
|
||||
|
||||
> **_Merksatz:_**
|
||||
> "$A$ gilt genau dann, wenn $B$ gilt"
|
||||
|
||||
| $A$ | $B$ | $A \Leftrightarrow B$ |
|
||||
| :---: | :---: | :-------------------: |
|
||||
| $0$ | $0$ | $1$ |
|
||||
| $0$ | $1$ | $0$ |
|
||||
| $1$ | $0$ | $0$ |
|
||||
| $1$ | $1$ | $1$ |
|
||||
|
||||
> **_Beispiel:_**
|
||||
> $A(x):=x^2=4$ und $B(x):=x=2$
|
||||
>
|
||||
> in $\mathbb{Z}$:
|
||||
> $$B(x) \Rightarrow A(x): wahr$$
|
||||
>
|
||||
> in $\mathbb{N}$:
|
||||
> $$A(x) \Rightarrow B(x): wahr$$
|
||||
> $$B(x) \Rightarrow A(x): wahr$$
|
||||
> $$A(x) \Leftrightarrow A(x): wahr$$
|
||||
|
||||
#### Reihenfolge der Bindungen
|
||||
Die Reihenfolge der Bindungen beschreibt, welcher Operator die höchste Priorität hat.
|
||||
|
||||
- $\neg$
|
||||
- $\wedge$
|
||||
- $\vee$
|
||||
- $\Rightarrow$
|
||||
- $\Leftrightarrow$
|
||||
|
||||
Wie zu sehen ist, hat $\neg$ die höchste Priorität. Schreibt man also eine Operation wie etwa $\neg A \wedge B$, muss $A$ negiert werden bevor die `AND` ($\wedge$)-operation berechnet wird: $(\neg A) \wedge B$.
|
||||
|
||||
Des weiteren hat `AND` ($\wedge$) eine höhere Priorität als `OR` ($\vee$). So muss also in der Rechnung $A \vee B \wedge C$ der Term $B \wedge C$ als erstes berechnet werden: $A \vee (B \wedge C)$.
|
||||
|
||||
#### Junktorenregeln
|
||||
Junktorenregeln sind Regeln, wie man Aussagen umformen kann, sodass die Aussage (bzw. deren Bedingungen und Resultat) dieselbe ist.
|
||||
|
||||
##### Regel der doppelten Negation
|
||||
$\neg\neg A \Leftrightarrow A$
|
||||
|
||||
##### Kommutativität
|
||||
$A \wedge B \Leftrightarrow B \wedge A$ und $A \vee B \Leftrightarrow B \vee A$
|
||||
|
||||
##### Assoziativität
|
||||
$(A \wedge B) \wedge C \Leftrightarrow A \wedge (B \wedge C)$
|
||||
$(A \vee B) \vee C \Leftrightarrow A \vee (B \vee C)$
|
||||
|
||||
##### Distributivität
|
||||
$A \wedge (B \vee C) \Leftrightarrow (A \wedge B) \vee (A \wedge C)$
|
||||
$A \vee (B \wedge C) \Leftrightarrow (A \vee B) \wedge (A \vee C)$
|
||||
|
||||
> **_Note:_**
|
||||
> Es kann helfen, sich beim Umformen der Rechenoperationen die herkömmlichen Operationen $\times$ (Mal) und $+$ (Plus) vorzustellen, um eine Idee davon zu bekommen, wie die Operation vereinfacht werden muss:
|
||||
>
|
||||
> $$\underbrace{A}_{x} \underbrace{\wedge}_{\times}(\underbrace{B}_{y} \underbrace{\vee}_{+} \underbrace{C}_{z})\\
|
||||
> x \times (y + z) \Leftrightarrow (x \times y) + (x \times z)$$
|
||||
> Verglichen mit:
|
||||
> $$(\overbrace{A}^{x} \overbrace{\wedge}^{\times} \overbrace{B}^{y}) \overbrace{\vee}^{+} (\overbrace{A}^{x} \overbrace{\wedge}^{\times} \overbrace{C}^{z})$$
|
||||
> Dieselbe Vorgangsweise lässt sich sowohl für Operationen mit $\wedge$ als auch mit $\vee$ anwenden:
|
||||
> $$\overbrace{A}^{x} \overbrace{\vee}^{\times}(\overbrace{B}^{y} \overbrace{\wedge}^{+} \overbrace{C}^{z}) \overbrace{\Rightarrow}^{\Rightarrow}
|
||||
> (\overbrace{A}^{x} \overbrace{\vee}^{\times} \overbrace{B}^{y}) \overbrace{\wedge}^{+} (\overbrace{A}^{x} \overbrace{\vee}^{\times} \overbrace{C}^{z})$$
|
||||
|
||||
##### Regeln von De Morgan
|
||||
$\neg (A \wedge B) \Leftrightarrow \neg A \vee \neg B$
|
||||
$\neg (A \vee B) \Leftrightarrow \neg A \wedge \neg B$
|
||||
|
||||
> **_Beispiel:_**
|
||||
> | Rechnung | Nächster Vorgang |
|
||||
> | ------------------------------------------------ | ----------------- |
|
||||
> | $A \Rightarrow B$ | |
|
||||
> | $\Leftrightarrow \neg A \vee B$ | |
|
||||
> | $\Leftrightarrow \neg\neg(\neg A \vee B)$ | Doppelte Negation |
|
||||
> | $\Leftrightarrow \neg(\neg\neg A \wedge \neg B)$ | De Morgan |
|
||||
> | $\Leftrightarrow \neg(A \wedge \neg B)$ | |
|
||||
> | $\Leftrightarrow \neg A \vee \neg\neg B$ | De Morgan |
|
||||
> | $\Leftrightarrow \neg\neg B \vee \neg A$ | Kommutativ |
|
||||
> | $\Leftrightarrow \neg B \Rightarrow \neg A$ | |
|
||||
|
||||
> **_In Worten:_**
|
||||
> "Wenn es regnet, ist die Wiese nass" ($A \Rightarrow B$)
|
||||
> "Wenn die Wiese nicht nass ist, regnet es nicht. ($\neg B \Rightarrow \neg A$)
|
||||
|
||||
> **_Hinweis:_**
|
||||
> Diese Umformung ($\neg B \Rightarrow \neg A$) ist nicht dasselbe wie $\neg(A \Rightarrow B)$
|
||||
>
|
||||
> Weil:
|
||||
> $$\neg(A \Rightarrow B)\\
|
||||
> \Leftrightarrow \neg(\neg A \vee B)\\
|
||||
> \Leftrightarrow \neg\neg A \wedge \neg B\\
|
||||
> \Leftrightarrow A \wedge \neg B$$
|
||||
|
||||
##### Kontraposition
|
||||
$$A \Rightarrow B \Leftrightarrow \neg B \Rightarrow \neg A$$
|
||||
|
||||
### Quantoren
|
||||
Weg um ein Prädikat in eine Aussage umzuformen.
|
||||
|
||||
**_Beispiel:_**
|
||||
$P(x):=\text{"x ist eine natürliche Zahl"}$: Prädikat
|
||||
$P(5):=\text{"5 ist eine natürliche Zahl"}$: Aussage
|
||||
|
||||
In dieser Aussage ist die Variable $x$ gebunden ($x = 5$).
|
||||
|
||||
$\text{"Es gibt mindestens ein }x \in \mathbb{Z}\text{, so dass }P(x)\text{ gilt."}$: Aussage
|
||||
$\text{"Für alle }x \in \mathbb{Z}\text{ gilt }P(x)$.": Aussage
|
||||
|
||||
Quantoren sind Symbole, anhand derer wir aus Prädikaten oder Aussagen gewinnen können. Wir betrachten das Beispiel des Prädikates:
|
||||
|
||||
$$A(x) := \text{"x ist eine Primzahl und x ist ein Teiler von 24"}$$
|
||||
$$B:=\text{"es gibt eine Primzahl welche ein Teiler von 24 ist"}$$
|
||||
|
||||
mit anderen Worten:
|
||||
|
||||
$$B:= \text{"Es existiert ein x mit A(x)".}$$
|
||||
|
||||
Ein n-stelliges Prädikat wird durch Quantifizierung stets zu einem neuen $n-1$ stelligen Prädikat
|
||||
|
||||
> **_Beispiel:_**
|
||||
> $$A(x, y):= x < y$$
|
||||
> Bei der Funktion $A$ handelt es sich um ein 2-stelliges Prädikat. Die beiden Parameter heissen $x$ und $y$.
|
||||
> $$B(y):= \forall x \in \mathbb{R} A(x, y)$$
|
||||
> Anders als die Funktion $A$ hat die Funktion $B$ nur einen Parameter namens $y$. Das Prädikat $B$ ist somit 1-stellig.
|
||||
|
||||
#### Operatoren
|
||||
Es gibt zwei verschiedene Quantoren, dessen Eigenschaften im Folgenden kurz aufgezeigt werden.
|
||||
|
||||
| Symbol | Bezeichnung | Beschreibung | Gesprochen |
|
||||
| --------- | --------------- | ----------------------------- | --------------- |
|
||||
| $\forall$ | Allquantor | universelle Quantifizierung | "für alle" |
|
||||
| $\exists$ | Existenzquantor | existenzielle Quantifizierung | "für mind. ein" |
|
||||
|
||||
> **_Beispiele:_**
|
||||
> $A(x, y) := x < y$
|
||||
> $\forall x \in \mathbb{R}(\exists y \in \mathbb{R} A(x, y))$
|
||||
> In Worten: "Für alle $x$ in den reellen Zahlen gibt es mindestens ein $y$, das grösser ist. Diese Aussage ist wahr.
|
||||
>
|
||||
> $B(x) := \text{"}x\text{ kann programmieren"}$
|
||||
> $I := Menge der Informatiker$
|
||||
> $A := \forall x \in I B(x) \Leftrightarrow \text{"Alle Informatiker können programmieren"}$
|
||||
> $\text{"Alles, was ein Informatiker ist, kann programmieren"}$
|
||||
> $\Leftrightarrow \forall x (x \in I \Rightarrow B(x))$
|
||||
|
||||
Ausdrücke wie $\forall_x \forall_y A(x, y)$ können zu $\forall_{x,y} A(x,y)$ gekürzt werden.
|
||||
|
||||
#### Regeln
|
||||
1. Klammern
|
||||
Quantoren binden stärker als Junktoren:
|
||||
$\forall x \in M B(x) \wedge C(x) \Leftrightarrow (\forall x \in M B(x)) \wedge C(x)$
|
||||
nicht dasselbe wie:
|
||||
$\forall x \in M (B(x) \wedge C(x))$
|
||||
|
||||
2. Abkürzungen
|
||||
$\forall x \in M (\forall y \in M A(x,y)) \Leftrightarrow \forall_{x,y} \in M A(x,y)$
|
||||
$\exists x \in M (\exists y \in M A(x,y)) \Leftrightarrow \exists_{x,y} \in M A8x,y)$
|
||||
Falls die Menge klar ist, kann diese von den Faktoren weggelassen werden:
|
||||
$\forall x A(x)$ statt $\forall x \in M A(x)$
|
||||
3. Negation
|
||||
$\neg \exists_x \in M A(x) \Leftrightarrow \forall_x \in M \neg A(x)$
|
||||
$\neg \forall_x \in M A(x) \Leftrightarrow \exists_in \in M \neg A(x)$
|
||||
|
||||
#### Beispielsätze
|
||||
|
||||
| In Worten | Operation |
|
||||
| ---------------------------------- | ------------------------------------------------------------------------------------------------------ |
|
||||
| Alle Prüfungen sind einfach | $\forall_x \in P E(x)$ |
|
||||
| Eine Prüfung ist einfach | $\exists_x \in P E(x)$ |
|
||||
| Keine Prüfung ist einfach | $\exists_x \in P E(x)$ |
|
||||
| Alle Prüfungen sind nicht einfach | $\forall_x \in P \neg E(x)$ |
|
||||
| Nur eine Prüfung ist einfach | $(\exists_x \in P E(x)) \wedge (\forall_{y,z} \in P (E(y) \wedge E(z) \Rightarrow y=z))$ |
|
||||
| Nur eine Prüfung ist nicht einfach | $(\exists_x \in P \neg E(x)) \wedge (\forall_{y,z} \in P (\neg E(y) \wedge \neg E(z) \Rightarrow y=z)$ |
|
||||
| Nicht alle Prüfungen sind einfach | $\neg \forall_x \in P E(x))$ |
|
||||
| Eine Prüfung ist nicht einfach | $\exists_x \in P \neg E(x)$ |
|
||||
|
||||
#### Vereinfachungen
|
||||
| Term | Vereinfachung |
|
||||
| ------------------------------------ | ---------------------- |
|
||||
| $\neg \exists_x \neg A(x)$ | $\forall_x A(x)$ |
|
||||
| $\neg \exists_x \in K \neg A(x)$ | $\forall_x \in K A(x)$ |
|
||||
| $\forall_x(x\in K \Rightarrow A(x))$ | $\forall_x \in K A(x)$ |
|
||||
| $\exists_x (x \in K \wedge A(x))$ | $\exists_x \in K A(x)$ |
|
||||
|
||||
## Grundlegende Beweistechniken
|
||||
### Direkter Beweis einer Implikation
|
||||
Es gilt, eine Implikation zu beweisen:
|
||||
$$A \Rightarrow B$$
|
||||
|
||||
Beweisen, dass in allen Fällen, in denen $A$ wahr ist, auch $B$ wahr ist.
|
||||
|
||||
Dies geschieht durch das Beweisen der Allgemeingültigkeit durch Nutzung von Variablen an Stelle von konkreten Werten.
|
||||
|
||||
> ***Beispiel:***
|
||||
> - $A$: "$x$ und $y$ sind gerade."
|
||||
> - $B$: "$x \cdot y$ ist gerade."
|
||||
> - $A \Rightarrow B$: "Wenn $x$ und $y$ gerade sind, ist auch $x \cdot y$ gerade.
|
||||
>
|
||||
> ***Beweis:***
|
||||
> $$x = 2 \cdot n_x$$
|
||||
> $$y = 2 \cdot n_y$$
|
||||
> $$x \cdot y = (2 \cdot n_x) \cdot (2 \cdot n_y)$$
|
||||
> $$\Leftrightarrow 2 \cdot (n_x \cdot 2 \cdot n_y)$$
|
||||
> $x \cdot y$ ist also durch 2 teilbar und ist somit gerade.
|
||||
|
||||
### Beweis durch Widerspruch
|
||||
Es gilt zu beweisen, dass eine Aussage $A$ wahr ist.
|
||||
|
||||
Die Lösungsstrategie hierbei ist, zu beweisen, dass die Negation der Aussage falsch ist.
|
||||
|
||||
> ***Beispiel:***
|
||||
> - $A$: "Es gibt keine grösste natürliche Zahl"
|
||||
>
|
||||
> Die negierte Annahme $A$, entspricht der, dass es eine grösste natürliche Zahl $m$ gibt.
|
||||
>
|
||||
> Für jede natürliche Zahl $n \in \mathbb{N}$ gilt, dass es einerseits eine nächstgrössere Natürliche Zahl $o = n + 1$ für die $o > n$ gilt.
|
||||
>
|
||||
> Da auch die angenommene grösste Zahl $m$ eine natürliche Zahl $n \in \mathbb{N}$ ist, gilt auch für $m$, dass es eine folgezahl $o$ gibt, die grösser ist. Dies kann als Beweis interpretiert werden, dass die Aussage $A$ wahr ist.
|
||||
|
||||
### Beweis durch (Gegen-)Beispiel
|
||||
Es gilt zu zeigen, dass eine bestimmte bestimmte Aussage nicht auf alle Elemente zutrifft.
|
||||
|
||||
Dies geschieht, indem man ein Beispiel oder ein Gegenbeispiel für die vorliegende Aussage findet.
|
||||
|
||||
> ***Beispiele in Worte:***
|
||||
> - $A$: "Alle Schweine sind rosa."
|
||||
> - Gegenbeispiel $B$: "Die Schweine, die Kenny getötet haben, sind aber nicht rosa!"
|
||||
>
|
||||
> - $A$: "Es gibt Wochentage, die nicht mit '-tag' enden."
|
||||
> - Beispiel $B$: "Mittwoch."
|
||||
|
||||
> ***Beispiel:***
|
||||
> - $A$: "Nicht jede natürliche Zahl ist eine Quadratzahl einer natürlichen Zahl."
|
||||
> oder in alternativer Ausdrucksweise:
|
||||
> $A$: "Es gibt natürliche Zahlen, die keine Quadratzahl einer natürlichen Zahl sind."
|
||||
>
|
||||
> Um diese Aussage $A$ zu belegen, gilt es lediglich, ein geeignetes Beispiel zu finden.
|
||||
>
|
||||
> Aufzeigen kann man das bspw. anhand der Zahl $2$.
|
||||
>
|
||||
> $1^2 = 1$ ist kleiner als $2$ und $2^2 = 4$ ist grösser als $2$. $2$ ist also keine Quadratzahl einer natürlichen Zahl.
|
||||
|
||||
### Beweis durch Kontraposition
|
||||
Es gilt zu beweisen, ob eine Aussage, welche eine Implikation in der Form $A \Rightarrow B$ (siehe [Implikation](#4-implikation)) ist, wahr oder falsch ist.
|
||||
|
||||
Dies kann erreicht werden, indem man, wie im Kapitel [Kontraposition](#kontraposition) beschrieben die Aussage von $A \Rightarrow B$ zu $\neg B \Rightarrow \neg A$ umformt.
|
||||
|
||||
> ***Beispiel in Worten:***
|
||||
> - $A$: "Wenn es regnet ist die Wiese nass."
|
||||
> - Beweisbare Kontraposition $B$: "Wenn die Wiese nicht nass ist, regnet es nicht."
|
||||
|
||||
> ***Beispiel:***
|
||||
> - $A$: "Für jede natürliche Zahl $n$ gilt: $(n^2 + 1 = 1) \Rightarrow (n = 0)$
|
||||
> - Kontraposition $B$: "Für jede natürliche Zahl $n$ gilt: $(n \not = 0) \Rightarrow (n^2 + 1 \not = 1)$
|
||||
>
|
||||
> Falls die Bedingung, dass $n \not = 0$ ist, gilt auch, dass $n^2 \not = 0$ ist.
|
||||
> Somit ist also bewiesen, dass, im Falle, dass $n \not = 0$, auch $n^2 + 1 \not = 1$ zutrifft.
|
||||
|
||||
### Beweis einer Äquivalenz
|
||||
Es ist eine Aussage der Form $A \Leftrightarrow B$ zu beweisen.
|
||||
|
||||
Erreicht werden kann das, indem man sowohl $A \Rightarrow B$ als auch $B \Rightarrow A$ beweist.
|
||||
|
||||
> ***Beispiel:***
|
||||
> - $A$: "$(n\text{ ist gerade}) \Leftrightarrow (n^2\text{ ist gerade})$"
|
||||
>
|
||||
> Eine gerade Zahl kann jeweils bestimmt werden, indem man eine bestehende Zahl verdoppelt:
|
||||
> $$n = 2 \cdot i$$
|
||||
> $n$ ist also immer dann gerade, wenn es $2 \cdot i$ entspricht ($i$ ist hierbei eine beliebige, natürliche Zahl).
|
||||
>
|
||||
> Trifft dies zu, so entspricht $n^2$ folgendem: $(2 \cdot i) \cdot (2 \cdot i)$.
|
||||
> Dies lässt sich, als Beweis, dass es durch $2$ teilbar ist, folgendermassen umformen:
|
||||
> $$2 \cdot (i \cdot 2 \cdot i)$$
|
||||
> Da $n^2$ immer dem Term $(2 \cdot i) \cdot (2 \cdot i)$ entspricht, ist diese Aussage nun in beide Richtungen bewiesen.
|
||||
|
||||
### Beispielübung
|
||||
Jeder Geldbetrag von mindestens $4$ Cents lässt sich alleine mit $2$- und $5$-Centstücken bezahlen.
|
||||
|
||||
In algebraischer Form würde das in etwa so aussehen:
|
||||
|
||||
$$\forall x \in \left\{ \mathbb{N} | x \geq 4 \right\} x = 2a + 5b$$
|
||||
|
||||
An dieser Stelle steht $a$ für die Anzahl $2$-Centstücke und $b$ für die Anzahl $5$-Centstücke.
|
||||
|
||||
Dies kann mit Hilfe einer Fallunterscheidung (basierend darauf, ob der zu bezahlende Betrag gerade oder ungerade ist).
|
||||
|
||||
Eine natürliche Zahl kann nur entweder gerade oder ungerade sein. Aus diesem Grund müssen nur diese beiden Fälle behandelt werden.
|
||||
|
||||
#### Für gerade Zahlen
|
||||
Gerade Zahlen können jeweils mit $2$-Centstücken bezahlt werden. Die Anzahl $2$-Centstücke ist hierbei jeweils der zu bezahlende Betrag geteilt durch $2$.
|
||||
|
||||
In algebraischer Form würde dies in etwa folgendermassen aussehen:
|
||||
$$\forall x \in \left\{ \mathbb{N} | x \geq 4 | x \text{ ist gerade} \right\} = 2 \cdot \frac{x}{2}$$
|
||||
|
||||
#### Für ungerade Zahlen
|
||||
Um ungerade Zahlen zu erreichen, muss ein Weg gefunden werden, zu einem bestehenden, geraden Betrag einen zusätzlichen Cent zu bezahlen.
|
||||
|
||||
Dies kann erreicht werden, indem man 2 $2$-Centstücke weniger als geplant und stattdessen ein zusätzliches $5$-Centstück auszahlt.
|
||||
|
||||
Algebraisch sieht das wiederum so aus:
|
||||
$$\forall x \in \left\{ \mathbb{N} | x \geq 4 | x \text{ ist ungerade} \right\} = 2 \cdot \left(\frac{x}{2} - 2\right) + 5 \cdot 1$$
|
||||
|
||||
Damit ist nun die getätigte Aussage dieser Aufgabe bewiesen.
|
||||
|
|
@ -0,0 +1,234 @@
|
|||
# Syntax & Semantik
|
||||
## Definition
|
||||
Die Syntax beschreibt jeweils die Form, in der Dinge niedergeschrieben oder abgespeichert sind, während die Semantik bedeutet, wie das Geschriebene/das Gespeicherte interpretiert wird.
|
||||
|
||||
Folgend einige Beispiele:
|
||||
|
||||
| Syntax | Semantik |
|
||||
| ---------------------------------- | ---------------------------------------------- |
|
||||
| Paritur | Musik (Schallwellen) |
|
||||
| Java-Code | Verhalten des Computers |
|
||||
| Terme einer mathematischen Theorie | Mathematische Objekte |
|
||||
| Aussagenlogische Formeln | Boolsche Funktionen |
|
||||
| Peano-Axiome | Die Struktur ($\mathbb{N}$, $+$, $\cdot$ etc.) |
|
||||
| Feynnman-Diagramm | Wechselwirkungen |
|
||||
|
||||
Abgesehen von den bereits aus dem Kapitel "Grundbegriffe und elementare Logik" bekannten Ausdrücke sind auch folgende Ausdrücke wichtig:
|
||||
- $\top$: Gleichbedeutend mit `true`
|
||||
- $\bot$: Gleichbedeutend mit `false`
|
||||
|
||||
## Darstellung
|
||||
Um leichter Erkenntnisse über Wahrheitswerte von Aussagen zu ziehen, können diese in verschiedene Darstellungsformen gebracht werden.
|
||||
|
||||
Im Folgenden werden einige davon aufgezeigt.
|
||||
|
||||
### Ableitungsbaum
|
||||
Ein Ableitungsbaum lässt es zu, den Überblick über eine Aussage bei einer bestimmten Belegung zu geben.
|
||||
|
||||
Folgende Formel gilt es darzustellen:
|
||||
$$f = (((a \wedge b) \vee (\neg c)) \wedge (a \vee b))$$
|
||||
|
||||
Folgendes ist der Ableitungsbaum unter der Bedingung, dass $a = 1$, $b = 0$ und $c = 0$ entspricht:
|
||||
|
||||
```mermaid
|
||||
flowchart BT;
|
||||
a((a: 1));
|
||||
b((b: 0));
|
||||
c((c: 0));
|
||||
a --- 1((AND));
|
||||
b --- 1;
|
||||
c --- 2((NOT));
|
||||
1 -- 0 --- 3((OR));
|
||||
2 -- 1 --- 3;
|
||||
a --- 4((OR));
|
||||
b --- 4;
|
||||
3 -- 1 --- 5((AND));
|
||||
4 -- 1 --- 5;
|
||||
5 --- f((f: 1))
|
||||
```
|
||||
|
||||
### Boolsche Funktionen
|
||||
Ein weiterer Weg, eine Aussage darzustellen ist als boolsche Funktionen.
|
||||
|
||||
Hierbei werden jeweils algebraische Operatoren durch eine Funktion ersetzt, die dasselbe aussagt, nämlich folgende:
|
||||
|
||||
| Operator | Funktion |
|
||||
| ------------ | ------------------ |
|
||||
| $\neg A$ | $\text{not}(A)$ |
|
||||
| $A \wedge B$ | $\text{or}(A, B)$ |
|
||||
| $A \vee B$ | $\text{and}(A, B)$ |
|
||||
|
||||
$$\begin{aligned}
|
||||
\newcommand{\and}{\mathop{\mathrm{and}}}
|
||||
\text{or}(x,y) &= \begin{cases}
|
||||
true & \text{falls} & x = true & \text{oder} & y = true \\
|
||||
false & \text{sonst}
|
||||
\end{cases} \\
|
||||
|
||||
\text{and}(x,y) &= \begin{cases}
|
||||
true & \text{falls} & x = true & \text{und} & y = true \\
|
||||
false & \text{sonst}
|
||||
\end{cases} \\
|
||||
|
||||
\text{not}(x) &= \begin{cases}
|
||||
true & \text{falls} & x = false \\
|
||||
false & \text{sonst}
|
||||
\end{cases}
|
||||
\end{aligned}$$
|
||||
|
||||
### Wahrheitstabelle
|
||||
Ein weiterer Weg, welcher es einem erleichtert, Erkenntnisse aus einer Aussage zu treffen, ist das Ausarbeiten einer Wahrheitstabelle, indem man alle einzelnen Terme berechnet.
|
||||
|
||||
Folgend ein Beispiel für diesen algebraischen Ausdruck:
|
||||
$$p_0 \rightarrow (q \vee p_1)$$
|
||||
|
||||
| $p_0$ | q | $p_1$ | $q \vee p_1$ | $p_0 \rightarrow (q \vee p_1)$ |
|
||||
| :---: | :---: | :---: | :----------: | :----------------------------: |
|
||||
| $0$ | $0$ | $0$ | $0$ | $1$ |
|
||||
| $0$ | $0$ | $1$ | $1$ | $1$ |
|
||||
| $0$ | $1$ | $0$ | $1$ | $1$ |
|
||||
| $0$ | $1$ | $1$ | $1$ | $1$ |
|
||||
| $1$ | $0$ | $0$ | $0$ | $0$ |
|
||||
| $1$ | $0$ | $1$ | $1$ | $1$ |
|
||||
| $1$ | $1$ | $0$ | $1$ | $1$ |
|
||||
| $1$ | $1$ | $1$ | $1$ | $1$ |
|
||||
|
||||
#### Boolsche Operatoren als Wahrheitstabellen
|
||||
Folgendes sind boolsche Operatoren dargestellt als Wahrheitstabellen.
|
||||
|
||||
##### `AND` $\wedge$
|
||||
| $F$ | $G$ | $F \wedge G$ |
|
||||
| :---: | :---: | :----------: |
|
||||
| $0$ | $0$ | $0$ |
|
||||
| $0$ | $1$ | $0$ |
|
||||
| $1$ | $0$ | $0$ |
|
||||
| $1$ | $1$ | $1$ |
|
||||
|
||||
##### `OR` $\vee$
|
||||
| $F$ | $G$ | $F \vee G$ |
|
||||
| :---: | :---: | :--------: |
|
||||
| $0$ | $0$ | $0$ |
|
||||
| $0$ | $1$ | $1$ |
|
||||
| $1$ | $0$ | $1$ |
|
||||
| $1$ | $1$ | $1$ |
|
||||
|
||||
##### Implikation $\Rightarrow$
|
||||
| $F$ | $G$ | $F \Rightarrow G$ |
|
||||
| :---: | :---: | :---------------: |
|
||||
| $0$ | $0$ | $1$ |
|
||||
| $0$ | $1$ | $1$ |
|
||||
| $1$ | $0$ | $0$ |
|
||||
| $1$ | $1$ | $1$ |
|
||||
|
||||
#### Negation $\neg$
|
||||
| $F$ | $\neg F$ |
|
||||
| :---: | :------: |
|
||||
| $0$ | $1$ |
|
||||
| $1$ | $0$ |
|
||||
|
||||
## Semantische Eigenschaften
|
||||
Über eine Formel $A$ mit der Belegung $B$ können unter bestimmten Umständen bestimmte Aussagen getroffen werden.
|
||||
|
||||
Folgend sind Aussagen und dazugehörige Umstände aufgelistet.
|
||||
|
||||
| Bezeichnung | Alternative Bezeichnung | Beschreibung |
|
||||
| ----------------- | --------------------------------- | ------------------------------------------------------------------------------ |
|
||||
| _Gültig_ | _richtig_ oder _wahr_ | Die gegebene Formel ist unter der Belegung $B$ wahr. |
|
||||
| _Allgemeingültig_ | _Tautologie_ oder _immer wahr_ | Die gegebene Formel ist, unabhängig der Belegung $B$, immer wahr. |
|
||||
| _Ungültig_ | _falsch_ oder _unwahr_ | Die gegebene Formel ist unter der Belegung $B$ nicht wahr. |
|
||||
| _Unerfüllbar_ | _Widerspruch_ oder _immer falsch_ | Die gegebene Formel ist, unabhängig der Belegung $B$, immer falsch. |
|
||||
| _erfüllbar_ | | Es gibt mindestens eine Belegung $B$ unter der die Formel erfüllbar ist. |
|
||||
| _widerlegbar_ | | Es gibt mindestens eine Belegung $B$ unter der die Formel nicht erfüllbar ist. |
|
||||
|
||||
## Normalformen
|
||||
Normalformen beinhalten generell nur `AND`s ($\wedge$), `OR`s ($\vee$) und `NOT`s ($\neg$).
|
||||
|
||||
### Negationsnormalform `NNF`
|
||||
Die Negationsnormalform (`NNF`) ist die Form einer Formel, in der nur atomare (nicht aufteilbare) Teilformeln negiert sind.
|
||||
|
||||
Folgendes Beispiel anhand dieser Formel:
|
||||
$$\neg(A \rightarrow (B \wedge \neg(C \vee D)))$$
|
||||
|
||||
Diese Form ist nicht komplett normalisiert, da sie den Operator $\rightarrow$ beinhaltet.
|
||||
Dieser Operator wird im Folgenden umgeformt.
|
||||
|
||||
$$\neg(\neg A \vee (B \wedge \neg(C \vee D)))$$
|
||||
|
||||
Diese Formel ist keine `NNF`, da 2 nicht-atomare Formeln negiert sind.
|
||||
Im Folgenden werden diese entfernt.
|
||||
|
||||
$$(\neg\neg A \wedge \neg(B \wedge (\neg C \wedge \neg D)))$$
|
||||
$$(\neg\neg A \wedge (\neg B \vee \neg(\neg C \wedge \neg D)))$$
|
||||
|
||||
Nun ist nur noch eine letzte nicht-atomare Teilformel negiert. Dieser Teil wird nun entfernt:
|
||||
|
||||
$$(\neg\neg A \wedge (\neg B \vee (\neg\neg C \vee \neg\neg D)))$$
|
||||
|
||||
In einem letzten Schritt werden nun doppelte Negationen weg vereinfacht:
|
||||
|
||||
$$(A \wedge (\neg B \vee (C \vee D)))$$
|
||||
|
||||
Bei dieser Formel handelt es sich nun um eine Negationsnormalform (`NNF`), da nur atomare Teilformeln negiert sind und nur $\neg$s, $\vee$s und $\wedge$s in der Formel genutzt werden.
|
||||
|
||||
### Disjunktive Normalform `DNF`
|
||||
Die Disjunktive Normalform ist eine Umformung der Formel, in der alle Belegungen für die die Formel $true$ ergibt, mit einander "verodert" werden.
|
||||
|
||||
Das sieht folgendermassen aus:
|
||||
|
||||
| $A$ | $B$ | $C$ | $D$ | $B \vee D$ | $(B \vee D) \wedge C$ | $\neg A \wedge ((B \vee D) \wedge C)$ |
|
||||
| :---: | :---: | :---: | :---: | :--------: | :-------------------: | :-----------------------------------: |
|
||||
| $0$ | $0$ | $0$ | $0$ | $0$ | $0$ | $0$ |
|
||||
| $0$ | $0$ | $0$ | $1$ | $1$ | $0$ | $0$ |
|
||||
| $0$ | $0$ | $1$ | $0$ | $0$ | $0$ | $0$ |
|
||||
| $0$ | $0$ | $1$ | $1$ | $1$ | $1$ | $1$ |
|
||||
| $0$ | $1$ | $0$ | $0$ | $1$ | $0$ | $0$ |
|
||||
| $0$ | $1$ | $0$ | $1$ | $1$ | $0$ | $0$ |
|
||||
| $0$ | $1$ | $1$ | $0$ | $1$ | $1$ | $1$ |
|
||||
| $0$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ |
|
||||
| $1$ | $0$ | $0$ | $0$ | $0$ | $0$ | $0$ |
|
||||
| $1$ | $0$ | $0$ | $1$ | $1$ | $0$ | $0$ |
|
||||
| $1$ | $0$ | $1$ | $0$ | $0$ | $0$ | $0$ |
|
||||
| $1$ | $0$ | $1$ | $1$ | $1$ | $1$ | $0$ |
|
||||
| $1$ | $1$ | $0$ | $0$ | $1$ | $0$ | $0$ |
|
||||
| $1$ | $1$ | $0$ | $1$ | $1$ | $0$ | $0$ |
|
||||
| $1$ | $1$ | $1$ | $0$ | $1$ | $1$ | $0$ |
|
||||
| $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $0$ |
|
||||
|
||||
Wie zu sehen ist, ist diese Formel an folgenden Stellen wahr:
|
||||
- $\neg A \wedge \neg B \wedge C \wedge D$
|
||||
- $\neg A \wedge B \wedge C \wedge \neg D$
|
||||
- $\neg A \wedge B \wedge C \wedge D$
|
||||
|
||||
Die `DNF` erreicht man nun die Teilformeln der genannten Stellen mit einem `OR` verknüpft:
|
||||
$$(\neg A \wedge \neg B \wedge C \wedge D) \vee (\neg A \wedge B \wedge C \wedge \neg D) \vee (\neg A \wedge B \wedge C \wedge D)$$
|
||||
|
||||
### Konjunktive Normalform `KNF`
|
||||
Bei der Konjunktiven Normalform wiederum, werden alle negierten Belegungen, in denen die gegebene Formel $false$ ergibt miteinander "geandet".
|
||||
|
||||
Folgendes wieder anhand eines realen Beispiels:
|
||||
|
||||
| $A$ | $B$ | $C$ | $A \vee C$ | $B \vee (A \wedge C)$ |
|
||||
| :---: | :---: | :---: | :--------: | :-------------------: |
|
||||
| $0$ | $0$ | $0$ | $0$ | $0$ |
|
||||
| $0$ | $0$ | $1$ | $0$ | $0$ |
|
||||
| $0$ | $1$ | $0$ | $0$ | $1$ |
|
||||
| $0$ | $1$ | $1$ | $0$ | $1$ |
|
||||
| $1$ | $0$ | $0$ | $0$ | $0$ |
|
||||
| $1$ | $0$ | $1$ | $1$ | $1$ |
|
||||
| $1$ | $1$ | $0$ | $0$ | $1$ |
|
||||
| $1$ | $1$ | $1$ | $1$ | $1$ |
|
||||
|
||||
An folgenden Stellen ergibt diese Formel $false$:
|
||||
- $\neg A \wedge \neg B \wedge \neg C$
|
||||
Negation: $A \vee B \vee C$
|
||||
- $\neg A \wedge \neg B \wedge C$
|
||||
Negation: $A \vee B \vee \neg C$
|
||||
- $A \wedge \neg B \wedge \neg C$
|
||||
Negation: $\neg A \vee B \vee C$
|
||||
|
||||
Um nun eine `KNF` zu erhalten müssen die Negationen der genannten Stellen mit dem $\vee$-Operator verknüpft werden:
|
||||
$$(A \vee B \vee C) \wedge (A \vee B \vee \neg C) \wedge (\neg A \vee B \vee C)$$
|
||||
|
||||
# Quellen
|
||||
- [YouTube - Konjunktive Normalform KNF / conjunctive normal form CNF | Digitaltechnik](https://www.youtube.com/watch?v=l6b7895U-u8)
|
||||
- [YouTube - Disjunktive Normalform DNF / disjunctive normal form | Digitaltechnik](https://www.youtube.com/watch?v=GyQITHPQst4)
|
||||
|
|
@ -0,0 +1,96 @@
|
|||
# Mengen, Relationen und Funktionen
|
||||
## Mengen
|
||||
Zusammenfassung **unterscheidbarer** Objekte
|
||||
|
||||
> **Beispiele:**
|
||||
> * Folgendes sind Mengen:
|
||||
> * ${1, 2, 3}$
|
||||
> * Mitglieder einer Klasse
|
||||
> * Wesen einer bestimmten Spezies
|
||||
> * Folgendes sind **keine** Mengen:
|
||||
> * ${1, 1, 3}$
|
||||
> * Personen mit schlechtem Gedankengut
|
||||
> * ***Anmerkung:*** Keine Menge, da der Term "schlecht" nicht genauer beschrieben wird
|
||||
|
||||
### Gleichheit von Mengen
|
||||
Zwei Mengen sind genau dann gleich, wenn die dieselben Elemente enthalten. Es gilt für alle Mengen $\mathbb{X}$ und $\mathbb{Y}$ die Äquivalenz, wenn folgendes zutrifft:
|
||||
|
||||
**Im Scrtipt nachlesen - Definition 15**
|
||||
|
||||
### Eigenschaften von Mengen
|
||||
#### Sortierung
|
||||
Mengen sind unsortiert folglich gilt folgendes:
|
||||
$$\{1,2,3\} = \{2,3,1\} = \{1,3,2\}$$
|
||||
|
||||
### Spezielle Zahlenmengen
|
||||
#### Natürliche Zahlen $\mathbb{N}$
|
||||
Die natürlichen zahlen beinhalten alle positiven, ganzen Zahlen.
|
||||
Üblicherweise ist in diesen die $0$ **nicht** mit eingeschlossen. Um dies eindeutig zu kennzeichnen, kann man die Menge auch als $\mathbb{N}_0$ schreiben.
|
||||
$$\mathbb{N} = \{\mathbb{N}_{\ge 1}\} = \{ 1, 2, 3, ...\}$$
|
||||
$$\mathbb{N}_0 = \{\mathbb{N}_{\ge 0}\} = \{ 0, 1, 2, 3, ... \}$$
|
||||
|
||||
#### Ganze Zahlen $\mathbb{Z}$
|
||||
$\mathbb{Z}$ beinhaltet alle ganzzahligen Werte. Des weiteren kann man die Menge $\mathbb{Z}$ in einer Notation schreiben, um klarzustellen, ob nur positive oder nur negative Zahlen gemeint sind ($\mathbb{Z}^+$ und $\mathbb{Z}^-$). Wird die Menge mit keiner besonderen Notation geschrieben, sind sowohl positive als auch negative Zahlen (inkl. $0$) gemeint.
|
||||
|
||||
$$\mathbb{Z} : \text{ganze Zahlen}$$
|
||||
$$\mathbb{Z} = \{..., -2, -1, 0, 1, 2 ...\}$$
|
||||
$$\mathbb{Z}^+ : \text{positive Zahlen}$$
|
||||
$$\mathbb{Z}^- : \text{negative Zahlen}$$
|
||||
|
||||
#### Rationale Zahlen $\mathbb{Q}$
|
||||
Rationale Zahlen sind Zahlen, die sich als einfacher Bruch darstellen lassen. So ist bspw. $\frac{1}{\sqrt{2}}$ **keine** rationale Zahl, da sich dieser Term nicht als einfacher Bruch darstellen lässt, denn $\sqrt{2}$ lässt sich nicht berechnen.
|
||||
|
||||
> ***Beispiele:***
|
||||
> $$\frac{2}{3}$$
|
||||
> $$\frac{1}{2}$$
|
||||
|
||||
#### Reelle Zahlen $\mathbb{R}$
|
||||
|
||||
$$\mathbb{R} : \text{reelle Zahlen}$$
|
||||
**Beispiele** $\sqrt{2}, \pi, e$
|
||||
$$\mathbb{C} : \text{komplexe Zahlen}$$
|
||||
Unmögliche Zahlen wie bspw. negaive Wurzeln
|
||||
|
||||
### Intervallschreibweise
|
||||
$$[a,b]:= \{ x \in \mathbb{R} | a \leq x \leq b \}$$
|
||||
|
||||
Falls in einer in der Intervallschreibweise geschriebenen Menge kein Definitionsbereich angegeben wird, wird implizit mit $\mathbb{R}$ (reellen Zahlen) gearbeitet.
|
||||
|
||||
$$]a, b[ = (a, b) = \{x\in \mathbb{R} | a < x < b\}$$
|
||||
|
||||
### Prädikatschreibweise
|
||||
|
||||
|
||||
## Relationen
|
||||
### Operationen auf Relationen
|
||||
1. Komposition $\circ$ (hintereinander ausführen)
|
||||
|
||||
$$R = \{(1, a), (2, b), (3, c)\} \subseteq A \times B$$
|
||||
|
||||
Surrjektiv - Rechtstotal
|
||||
Zu jedem "b" hat es mindestens ein "a"
|
||||
|
||||
Injektiv - Linkseindeutig
|
||||
Zu jedem "b" gibt es maximal ein "a"
|
||||
|
||||
Bijektiv (Surjektiv & ijketiv)
|
||||
Zu jedem "b" gibt es genau ein "a"
|
||||
|
||||
### Unendlich grosse Mengen
|
||||
Endlich grosse Mengen lassen sich vergleichen, indem man die Mächtigkeit gegenüberstellt - also die Anzahl der Elemente in $A$ und die Anzahl Elemente in $B$ und diese vergleicht.
|
||||
|
||||
In unendlich grossen Mengen ist dies jedoch unmöglich.
|
||||
|
||||
#### Abzählbarkeit
|
||||
1. Jede endliche Menge ist abzählbar
|
||||
2. Jede Teilmenge ist abzählbar
|
||||
3. Ist $X$ eine abzählbare Menge & gibt es eine surjektive Funktion $F: X \rightarrow Y$, dann ist auch $Y$ abzählbar
|
||||
4. Gibt es keine solche Funktion, ist $Y$ überabzählbar
|
||||
|
||||
Beispiele von Menge:
|
||||
- Abzählbar
|
||||
- $\mathbb{M}$, $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{N} \times \mathbb{N}$
|
||||
|
||||
## 2021-11-23
|
||||
- Beweismethode kleinster Verbrecher (Script Beispiel 50)
|
||||
-
|
||||
|
|
@ -0,0 +1,21 @@
|
|||
## 5.2 Primzahlen
|
||||
Primzahlen $p$ sind natürliche Zahlen ($\mathbb{N}$), die nur durch 1 und sich selbst teilbar sind.
|
||||
|
||||
D.h. Die Anzahl an Teilern, die eine Primzahl hat, **muss** $2$ entsprechen.
|
||||
|
||||
Dementsprechend ist $1$ keine Primzahl, da $1$ nur durch eine Zahl teilbar ist.
|
||||
|
||||
Primzahlen mit dem Sieb des Eratosthenes
|
||||
|
||||
### Beweisführung für unendliche Primzahlen
|
||||
Es gibt unendlich grosse Primzahlen
|
||||
|
||||
Beweis: Widerspruch
|
||||
Behauptung: Es gibt nur endlich viele Primzahlen $\mathbb{P} = \{p_1, ..., p_n} | p_i \in \mathbb{N}$
|
||||
|
||||
Aus satz 25:
|
||||
|
||||
### Primfaktoren Zerlegung
|
||||
Jede natürliche Zahl > 1 ist ein Produkt von endlich vielen Primzahlen.
|
||||
|
||||
Mit Hilfe der Primfaktorzerlegung lassen sich
|
||||
1
Notes/Semester 1/DM - Diskrete Mathematik/Q&A.md
Normal file
|
|
@ -0,0 +1 @@
|
|||
In welchen Situationen wird $\rightarrow$ und in welchen Situationen $\Rightarrow$ verwendet?
|
||||
|
|
@ -0,0 +1,4 @@
|
|||
# Inhaltsverzeichnis
|
||||
- [Grundbegriffe und elementare Logik](./01-Gundbegriffe%20und%20elementare%20Logik.md)
|
||||
- [Syntax & Semantik](./02-Syntax%20&%20Semantik.md)
|
||||
- [Mengen, Relationen und Funktionen](./03-Mengen,%20Relationen%20und%20Funktionen.md)
|
||||
479
Notes/Semester 1/DM - Diskrete Mathematik/Zusammenfassung.md
Normal file
|
|
@ -0,0 +1,479 @@
|
|||
<style>
|
||||
img[alt=mini] {
|
||||
max-height: 100px;
|
||||
}
|
||||
</style>
|
||||
# Inhaltsverzeichnis
|
||||
- [Inhaltsverzeichnis](#inhaltsverzeichnis)
|
||||
- [Aussagenlogisches Rechnen](#aussagenlogisches-rechnen)
|
||||
- [Operatoren](#operatoren)
|
||||
- [Regeln](#regeln)
|
||||
- [Regeln der Doppelten Negation](#regeln-der-doppelten-negation)
|
||||
- [Absorption](#absorption)
|
||||
- [Kommutativität](#kommutativität)
|
||||
- [Assoziativität](#assoziativität)
|
||||
- [Distributivität](#distributivität)
|
||||
- [Regeln von De Morgan](#regeln-von-de-morgan)
|
||||
- [Quantoren](#quantoren)
|
||||
- [Regeln](#regeln-1)
|
||||
- [Beweistechniken](#beweistechniken)
|
||||
- [Beweis durch Implikation](#beweis-durch-implikation)
|
||||
- [Beweis durch Widerspruch](#beweis-durch-widerspruch)
|
||||
- [Beweis durch (Gegen-)Beispiel](#beweis-durch-gegen-beispiel)
|
||||
- [Beweis durch Kontraposition](#beweis-durch-kontraposition)
|
||||
- [Beweis durch Äquivalenz](#beweis-durch-äquivalenz)
|
||||
- [Wahrheitstabelle](#wahrheitstabelle)
|
||||
- [Normalformen](#normalformen)
|
||||
- [Negationsnormalform `NNF`](#negationsnormalform-nnf)
|
||||
- [Disjunktive Normalform `DNF`](#disjunktive-normalform-dnf)
|
||||
- [Konjunktive Normalform `KNF`](#konjunktive-normalform-knf)
|
||||
- [Ableitungsbaum](#ableitungsbaum)
|
||||
- [Mengen](#mengen)
|
||||
- [Syntax](#syntax)
|
||||
- [Operationen](#operationen)
|
||||
- [Subset $\subseteq$](#subset-subseteq)
|
||||
- [Vereinigung $\cup$](#vereinigung-cup)
|
||||
- [Schnittmenge $\cap$](#schnittmenge-cap)
|
||||
- [Differenz $\setminus$](#differenz-setminus)
|
||||
- [Komplement/Negation $\overline{A}$](#komplementnegation-overlinea)
|
||||
- [Symmetrische Differenz $\triangle$](#symmetrische-differenz-triangle)
|
||||
- [Mächtigkeit $\vert A \vert$](#mächtigkeit-vert-a-vert)
|
||||
- [Kartesisches Produkt $\times$](#kartesisches-produkt-times)
|
||||
- [Rechenregeln](#rechenregeln)
|
||||
- [Kommuntativität](#kommuntativität)
|
||||
- [Vordefinierte Mengen](#vordefinierte-mengen)
|
||||
- [Potenzmenge $\mathcal{P}$](#potenzmenge-mathcalp)
|
||||
- [Partition](#partition)
|
||||
- [Unendlichkeit](#unendlichkeit)
|
||||
- [Rechnen mit Unendlichkeit](#rechnen-mit-unendlichkeit)
|
||||
- [Relationen](#relationen)
|
||||
- [Äquivalenzklasse](#äquivalenzklasse)
|
||||
- [Äquivalenzrelation](#äquivalenzrelation)
|
||||
- [Themen](#themen)
|
||||
- [Glossar](#glossar)
|
||||
|
||||
# Aussagenlogisches Rechnen
|
||||
## Operatoren
|
||||
- $\neg A$
|
||||
Gesprochen: "Nicht $A$"
|
||||
- $A \wedge B$
|
||||
Gesprochen: "$A$ und $B$"
|
||||
- $A \vee B$
|
||||
Gesprochen: "$A$ oder $B$"
|
||||
- $A \Rightarrow B$
|
||||
Entspricht $\neg A \vee B$. Gesprochen: "$A$ impliziert $B$"
|
||||
- $A \Leftrightarrow B$
|
||||
Gesprochen: "$A$ äquivalent $B$"
|
||||
|
||||
## Regeln
|
||||
### Regeln der Doppelten Negation
|
||||
$$\neg\neg A \Leftrightarrow A$$
|
||||
|
||||
### Absorption
|
||||
$$A \wedge A \Leftrightarrow A$$
|
||||
$$A \vee A \Leftrightarrow A$$
|
||||
|
||||
### Kommutativität
|
||||
Operanden können beliebig vertauscht werden:
|
||||
|
||||
$$A \wedge B \Leftrightarrow B \wedge A$$
|
||||
$$A \vee B \Leftrightarrow B \vee A$$
|
||||
|
||||
### Assoziativität
|
||||
**Identische** Operationen können in beliebiger Reihenfolge ausgeführt werden:
|
||||
|
||||
$$(A \wedge B) \wedge C \Leftrightarrow A \wedge (B \wedge C)$$
|
||||
$$(A \vee B) \vee C \Leftrightarrow A \vee (B \vee C)$$
|
||||
|
||||
### Distributivität
|
||||
**Unterschiedliche** Operationen können "ausmultipliziert" werden:
|
||||
|
||||
$$A \wedge (B \vee C) \Leftrightarrow (A \wedge B) \vee (A \wedge C)$$
|
||||
$$A \vee (B \wedge C) \Leftrightarrow (A \vee B) \wedge (A \vee C)$$
|
||||
|
||||
### Regeln von De Morgan
|
||||
$$\neg(A \wedge B) \Leftrightarrow \neg A \vee \neg B$$
|
||||
$$\neg(A \vee B) \Leftrightarrow \neg A \wedge \neg B$$
|
||||
|
||||
## Quantoren
|
||||
- $\forall x\, A(x)$
|
||||
Gesprochen: "Für alle $x$ gilt $A(x)$"
|
||||
- $\forall x \in M A(x)$
|
||||
Gesprochen: "Für alle $x$ aus der Menge $M$ gilt $A(x)$
|
||||
- $\exists x\, A(x)$
|
||||
Gesprochen: "Es gibt ein $x$ mit $A(x)$"
|
||||
- $\exists x \in M A(x)$
|
||||
Gesprochen: "Es gibt ein $x$ aus der Menge $M$ mit $A(x)$"
|
||||
|
||||
$\forall x \forall y\, A(x,y) \Leftrightarrow \forall{x,y}\, A(x,y)$ und $\exist x \exist y\, A(x,y) \Leftrightarrow \exist{x,y}\, A(x,y)$
|
||||
|
||||
> ***Hinweis:***
|
||||
> Die Bezeichnung fär die Symbole $\forall$ und $\exist$ sind _Allquantor_ und _Existenzquantor_.
|
||||
|
||||
### Regeln
|
||||
- Vertauschungsregel für unbeschränkte Quantoren
|
||||
$\forall x\, A(x) \Leftrightarrow \neg\exist x\, \neg A(x)$
|
||||
- Vertauschungsregel für beschränkte Quantoren
|
||||
$\forall x \in K\, A(x) \Leftrightarrow \neg\exist x \in K \neg A(x)$
|
||||
- Beschränkter und unbeschränkter Allquantor
|
||||
$\forall x \in K A(x) \Leftrightarrow \forall x(x \in K \Rightarrow A(x))$
|
||||
- Beschränkter und unbeschränkter Existenzquantor
|
||||
$\exist x K A(x) \Leftrightarrow \exist x(x \in K \wedge A(x))$
|
||||
|
||||
# Beweistechniken
|
||||
## Beweis durch Implikation
|
||||
Anwendbar bei Formeln in der Form:
|
||||
$$A \Rightarrow B$$
|
||||
|
||||
1. Zwingende Voraussetzungen für die Bedingung $A$ erfassen
|
||||
2. Prüfen, ob $B$ richtig ist
|
||||
|
||||
> ***Beispiel:***
|
||||
> $A$: "$x$ und $y$ sind gerade."
|
||||
> $B$: "$x \cdot y$ ist gerade."
|
||||
>
|
||||
> Damit $x$ und $y$ gerade sind, müssen sie ein Produkt von $2$ sein. Die Behauptung ist also:
|
||||
>
|
||||
> $x = 2 \cdot n_x$ und $y = 2 \cdot n_y$
|
||||
>
|
||||
> $n_x$ und $n_y$ sind hierbei **beliebige** natürliche Zahlen.
|
||||
>
|
||||
> Für den Nachweis ergibt sich folgendes für $B$:
|
||||
> $$x \cdot y = (2 \cdot n_x) \cdot (2 \cdot n_y) = 22 \cdot (n_x \cdot 2 \cdot n_y)$$
|
||||
> Da das Ergebnis ein vielfaches von $2$ ist, heisst das, dass $x \cdot y$ gerade ist und somit die Aussage $A \Rightarrow B$ wahr ist.
|
||||
|
||||
## Beweis durch Widerspruch
|
||||
Anwendbar bei einfachen Aussagen.
|
||||
|
||||
Der Merksatz ist hierbei: "Wenn die Aussage _nicht nicht wahr_ ist, ist sie _wahr_."
|
||||
|
||||
Der Vorgang ist hierbei, die ursprüngliche Aussage zu negieren und zu beweisen, dass die negierte Aussage **unerfüllbar** ist.
|
||||
|
||||
> ***Beispiel:***
|
||||
> $A$: "Es gibt keine grösste natürliche Zahl."
|
||||
> $\neg A$: "Es gibt **eine** grösste natürliche Zahl."
|
||||
>
|
||||
> $m$ sei dei grösste natürliche Zahl. Für jede natürliche Zahl $x$ gibt es ein Inkrement, welches man mit Hilfe von $x + 1$ errechnen kann. So gibt es auch für $m$ ein Inkrement $m + 1$, welches um $1$ grösser ist als $m$. Somit sit die negierte Aussage $\neg A$ **unerfüllbar**. $A$ ist wahr.
|
||||
|
||||
## Beweis durch (Gegen-)Beispiel
|
||||
Anwendbar bei Aussagen mit Quantoren ($\forall$ "für alle" und $\exists$ "existiert").
|
||||
|
||||
Die Strategie hierbei ist, ein anwendbares Beispiel (im Falle $\exists$) oder Gegenbeispiel (im Falle $\forall$) zu finden.
|
||||
|
||||
> ***Beispiel:***
|
||||
> $A$: "Es existieren Zahlen, welche kein Quadrat einer natürlichen Zahl sind."
|
||||
>
|
||||
> Dies lässt sich an dem Beispiel $2$ beweisen. $2$ ist weder ein Quadrat von $1$ ($1^2 = 1$) noch von $2$ ($2^2 = 4)$.
|
||||
|
||||
## Beweis durch Kontraposition
|
||||
Anwendbar bei Aussagen in der Form $A \Rightarrow B$
|
||||
|
||||
Es gilt für diese Strategie, die dazugehörige Kontraposition $\neg B \Rightarrow \neg A$ zu belegen.
|
||||
|
||||
> ***Beispiel:***
|
||||
> $A$: "Für jede natürliche Zahl $n$ gilt: $(n^2 + 1 = 1) \Rightarrow (n = 0)$
|
||||
>
|
||||
> Die Kontraposition dazu lautet wie folgt:
|
||||
> $A'$: "Für alle Zahlen, die **nicht** $0$ sind gilt $n^2 + 1 \not= 1$
|
||||
>
|
||||
> Da alle Zahlen $> 0$ ein Quadrat haben, das grösser als $0$ ist, gilt: $n^2 + 1 > 1$.
|
||||
> Daraus folgt, dass Aussage $A$ wahr ist.
|
||||
|
||||
## Beweis durch Äquivalenz
|
||||
Anwendbar für Aussagen der Form $A \Leftrightarrow B$
|
||||
|
||||
Die Strategie ist hierbei, zu beweisen, dass $A \Rightarrow B$ gilt und $B \Rightarrow A$ gilt.
|
||||
|
||||
> ***Beispiel:***
|
||||
> $A: (n^2 + 1 = 1) \Leftrightarrow (n = 0)$
|
||||
>
|
||||
> Wenn $n = 0$ ist, ergibt sich aus $(n^2 + 1 = 1)$ folgendes: $(0^2 + 1 = 1) = (0 + 1 = 1)$. Damit ist $A \Rightarrow B$ bewiesen.
|
||||
>
|
||||
> Die einzige Situation in der $(n^2 + 1 = 1)$ oder eher $(n^2 = 0)$ ergibt, ist, wenn $n$ $0$ entspricht. Damit ist auch $B \Rightarrow A$ bewiesen.
|
||||
|
||||
## Wahrheitstabelle
|
||||
Folgend ein Beispiel einer Wahrheitstabelle:
|
||||
|
||||
| $a$ | $b$ | $c$ | $b \vee c$ | $a \Rightarrow (b \vee c)$ |
|
||||
| :---: | :---: | :---: | :--------: | :------------------------: |
|
||||
| $0$ | $0$ | $0$ | $0$ | $1$ |
|
||||
| $0$ | $0$ | $1$ | $1$ | $1$ |
|
||||
| $0$ | $1$ | $0$ | $1$ | $1$ |
|
||||
| $0$ | $1$ | $1$ | $1$ | $1$ |
|
||||
| $1$ | $0$ | $0$ | $0$ | $0$ |
|
||||
| $1$ | $0$ | $1$ | $1$ | $1$ |
|
||||
| $1$ | $1$ | $0$ | $1$ | $1$ |
|
||||
| $1$ | $1$ | $1$ | $1$ | $1$ |
|
||||
|
||||
## Normalformen
|
||||
Normalformen beinhalten generell nur `AND`s ($\wedge$), `OR`s ($\vee$) und `NOT`s ($\neg$)
|
||||
|
||||
### Negationsnormalform `NNF`
|
||||
Die Negationsnormalform (`NNF`) ist die Form einer Formel, in der nur atomare (nicht aufteilbare) Teilformeln negiert sind.
|
||||
|
||||
> ***Beispiel:***
|
||||
> $$(A \wedge (\neg B \vee (C \vee D)))$$
|
||||
> Merke, dass nur $B$, welches _atomar_ ist, negiert ist.
|
||||
|
||||
### Disjunktive Normalform `DNF`
|
||||
Die Disjunktive Normalform ist eine Umformung der Formel, in der alle Belegungen für die die Formel $true$ ergibt, mit einander "verodert" werden.
|
||||
|
||||
> ***Beispiel:***
|
||||
> Die `DNF` für die Formel $\neg A \wedge (B \vee C)$ lautet folgendermassen:
|
||||
>
|
||||
> $$(\neg A \wedge \neg B \wedge C) \vee (\neg A \wedge B \wedge \neg C) \vee (\neg A \wedge B \wedge C)$$
|
||||
>
|
||||
> ***Herleitung:***
|
||||
> Schritt 1: Wahrheitstabelle aufstellen:
|
||||
> | $A$ | $B$ | $C$ | $B \vee C$ | $\neg A \wedge (B \vee C)$ |
|
||||
> | :---: | :---: | :---: | :--------: | :------------------------: |
|
||||
> | $0$ | $0$ | $0$ | $0$ | $0$ |
|
||||
> | $0$ | $0$ | $1$ | $1$ | $1$ |
|
||||
> | $0$ | $1$ | $0$ | $1$ | $1$ |
|
||||
> | $0$ | $1$ | $1$ | $1$ | $1$ |
|
||||
> | $1$ | $0$ | $0$ | $0$ | $0$ |
|
||||
> | $1$ | $0$ | $1$ | $1$ | $0$ |
|
||||
> | $1$ | $1$ | $0$ | $1$ | $0$ |
|
||||
> | $1$ | $1$ | $1$ | $1$ | $0$ |
|
||||
>
|
||||
> Schritt 2: $1$-Stellen aufschreiben:
|
||||
> - $\neg A \wedge \neg B \wedge C$
|
||||
> - $\neg A \wedge B \wedge \neg C$
|
||||
> - $\neg A \wedge B \wedge C$
|
||||
>
|
||||
> Schritt 3: Formeln für $1$-Stellen "verodern":
|
||||
> $$(\neg A \wedge \neg B \wedge C) \vee (\neg A \wedge B \wedge \neg C) \vee (\neg A \wedge B \wedge C)$$
|
||||
|
||||
### Konjunktive Normalform `KNF`
|
||||
Bei der Konjunktiven Normalform wiederum, werden alle negierten Belegungen, in denen die gegebene Formel $false$ ergibt miteinander "geandet".
|
||||
|
||||
> ***Beispiel:***
|
||||
> Der `KNF` von $B \vee (A \wedge C)$ ist:
|
||||
> $$(A \vee B \vee C) \wedge (A \vee B \vee \neg C) \wedge (\neg A \vee B \vee C)$$
|
||||
>
|
||||
> ***Herleitung:***
|
||||
> Schritt 1: Wahrheitstabelle aufstellen:
|
||||
> | $A$ | $B$ | $C$ | $A \vee C$ | $B \vee (A \wedge C)$ |
|
||||
> | :---: | :---: | :---: | :--------: | :-------------------: |
|
||||
> | $0$ | $0$ | $0$ | $0$ | $0$ |
|
||||
> | $0$ | $0$ | $1$ | $0$ | $0$ |
|
||||
> | $0$ | $1$ | $0$ | $0$ | $1$ |
|
||||
> | $0$ | $1$ | $1$ | $0$ | $1$ |
|
||||
> | $1$ | $0$ | $0$ | $0$ | $0$ |
|
||||
> | $1$ | $0$ | $1$ | $1$ | $1$ |
|
||||
> | $1$ | $1$ | $0$ | $0$ | $1$ |
|
||||
> | $1$ | $1$ | $1$ | $1$ | $1$ |
|
||||
>
|
||||
> Schritt 2: $0$-Stellen aufschreiben **und negieren**:
|
||||
> - $\neg A \wedge \neg B \wedge \neg C$
|
||||
> Negation: $A \vee B \vee C$
|
||||
> - $\neg A \wedge \neg B \wedge C$
|
||||
> Negation: $A \vee B \vee \neg C$
|
||||
> - $A \wedge \neg B \wedge \neg C$
|
||||
> Negation: $\neg A \vee B \vee C$
|
||||
>
|
||||
> Schritt 3: Negierte Ausdrücke mit `AND`s verketten:
|
||||
> $$(A \vee B \vee C) \wedge (A \vee B \vee \neg C) \wedge (\neg A \vee B \vee C)$$
|
||||
|
||||
## Ableitungsbaum
|
||||
Der Ableitungsbaum bietet einen übersichtlichen Weg um Gleichungen in der Aussagenlogik zu lösen.
|
||||
|
||||
Folgend ein Beispiel:
|
||||
|
||||
Es sei $(x \Rightarrow y) \wedge z$ mit folgender Belegung:
|
||||
- $B(x) = \top$
|
||||
- $B(y) = \bot$
|
||||
- $B(z) = \top$
|
||||
|
||||
Der dazugehörige Ableitungsbaum ist dann:
|
||||
|
||||
```mermaid
|
||||
flowchart BT
|
||||
op3(("∧: 0"))
|
||||
op2(("∨: 0"))
|
||||
op1(("¬: 0"))
|
||||
x["x: 1"]
|
||||
y["y: 0"]
|
||||
z["z: 1"]
|
||||
x --- op1
|
||||
op1 --- op2
|
||||
y --- op2
|
||||
op2 --- op3
|
||||
z --- op3
|
||||
```
|
||||
|
||||
# Mengen
|
||||
Mengen haben keine Sortierung und keine doppelten Elemente.
|
||||
|
||||
> ***Hinweise:***
|
||||
> - Mengen heissen "disjunkt", wenn sie **keine gemeinsamen** Elemente beinhalten.
|
||||
|
||||
## Syntax
|
||||
$M = \{ x \in \N | x > 5\}$
|
||||
|
||||
- $\in$
|
||||
Gesprochen: "Element von"
|
||||
- $\notin$
|
||||
Gesprochen: "Nicht Element von"
|
||||
- $|$
|
||||
Gesprochen: "Für die gilt"
|
||||
|
||||
"$M$ ist die Menge aller $x$, für die gilt, dass $x > 5$ ist."
|
||||
|
||||
$M = { 5, 6, 7, 8, ... }$
|
||||
|
||||

|
||||
|
||||
## Operationen
|
||||
### Subset $\subseteq$
|
||||
### Vereinigung $\cup$
|
||||
Die Vereinigung "Union" beschreibt die Zusammenfassung zweier Mengen:
|
||||
|
||||

|
||||
|
||||
### Schnittmenge $\cap$
|
||||
Die Schnittmenge "Intersection" zweier Mengen:
|
||||
|
||||

|
||||
|
||||
### Differenz $\setminus$
|
||||
Beschreibt die Differenzmenge zweier Mengen:
|
||||
|
||||

|
||||
|
||||
$A \setminus B$ gesprochen: "$A$ ohne $B$"
|
||||
|
||||
### Komplement/Negation $\overline{A}$
|
||||
Das Komplement einer Menge $A$ wird wie folgt geschrieben:
|
||||
$$\overline{A}$$
|
||||
|
||||
Sie beschreibt alle Elemente, die _nicht_ in der Menge $A$ vorkommen:
|
||||
|
||||

|
||||
|
||||
### Symmetrische Differenz $\triangle$
|
||||
Die Vereinigung zweier Mengen abzüglich deren Schnittmenge:
|
||||
|
||||

|
||||
|
||||
$A \triangle B = (A \setminus B) \cup (B \setminus A)$ gesprochen "$A$ ohne $B$ vereinigt mit $B$ ohne $A$"
|
||||
|
||||
### Mächtigkeit $\vert A \vert$
|
||||
Die Mächtigkeit $\vert A \vert$ beschreibt, wieviele Elemente eine Menge $A$ beinhaltet.
|
||||
|
||||
> ***Beispiel:***
|
||||
> $\vert \{1, 78, 28\} \vert = 3$
|
||||
|
||||
### Kartesisches Produkt $\times$
|
||||
Das Kartesische Produkt ist eine Menge aller Folgen, die aus den Elementen der beiden Mengen gebildet werden können.
|
||||
|
||||
Beispiel:
|
||||
$$A = \{a, b\}$$
|
||||
$$B = \{2, 3, 4\}$$
|
||||
$$A \times B = \{a, b\} \times \{2, 3, 4\} = \{(a, 2), (a, 3), (a, 4), (b, 2), (b, 3), (b, 4)\}$$
|
||||
|
||||
Die Mächtigkeit von $A \times B$ ist gleich $\vert A \vert \cdot \vert B \vert$
|
||||
|
||||
> ***Hinweis:***
|
||||
> **Folgen** sind sortiert das bedeutet folgendes:
|
||||
> $$A \times B \not = B \times A$$
|
||||
|
||||
## Rechenregeln
|
||||
### Kommuntativität
|
||||
|
||||
## Vordefinierte Mengen
|
||||
- $\N$: Natürliche Zahlen - Zahlen $\geq 0$
|
||||
- $\Z$: Alle ganzen Zahlen (positiv und negativ)
|
||||
|
||||
## Potenzmenge $\mathcal{P}$
|
||||
Die Potenzmenge gibt alle möglichen Kombinationen aus einer gegebenen Menge zurück. Die Funktion $\mathcal{P}(x)$ ist folgendermassen definiert:
|
||||
|
||||
$$\mathcal{P}(A) := \{x | x \subseteq A \}$$
|
||||
|
||||
> ***Beispiel:***
|
||||
> $$\mathcal{P}(\{0, 1\}) = \{\emptyset, \{0\}, \{1\}, \{0, 1\}\}$$
|
||||
|
||||
> ***Bemerkung:***
|
||||
> Die Mächtigkeit einer Potenzmenge errechnet sich folgendermassen:
|
||||
> $$|\mathcal{P}(A)| = 2^{|A|}$$
|
||||
|
||||
## Partition
|
||||
Eine Partition einer Menge $A$ ist eine Menge von Teilmengen von $A$.
|
||||
|
||||
Diese Teilmengen müssen folgende Bedingungen erfüllen:
|
||||
- Die Mengen dürfen nicht leer sein
|
||||
- Teilmengen dürfen untereinander keine gemeinsamen Elemente haben
|
||||
|
||||
## Unendlichkeit
|
||||
Unendliche Mengen sind unter folgenden Bedingungen abzählbar oder überabzählbar:
|
||||
|
||||
- Abzählbar unendlich, wenn sie gleich mächtig wie $\N$ sind
|
||||
- Überabzählbar unendlich, wenn sie mächtiger als $\N$ sind
|
||||
|
||||
### Rechnen mit Unendlichkeit
|
||||
$A$ sei eine abzählbar unendliche und $B$ eine überabzählbar unendliche Menge:
|
||||
|
||||
- $A \cup B$ ist **abzählbar**, da im Ergebnis nur Elemente aus der abzählbaren Menge $A$ enthalten sind.
|
||||
- $A \cap B$ ist **überabzählbar**, da alle Elemente der überabzählbaren Menge $B$ im Ergebnis enthalten sind
|
||||
- $B \setminus A$ ist **überabzählbar**, da von der überabzählbaren Menge $B$ nur die abzählbaren Elemente abgezogen werden.
|
||||
|
||||
# Relationen
|
||||
DAG ("discrete acyclic graph") ein "gerichteter azyklischer Graph" ist ein Graph, in dem keine Zyklen enthalten sind:
|
||||
|
||||
Folgendes ist ein DAG:
|
||||
|
||||
```mermaid
|
||||
flowchart LR
|
||||
a((A))
|
||||
b((B))
|
||||
c((C))
|
||||
d((D))
|
||||
e((E))
|
||||
f((F))
|
||||
g((G))
|
||||
a --> b
|
||||
b --> c
|
||||
c --> e
|
||||
b --> e
|
||||
b --> d
|
||||
g --> d
|
||||
d --> e
|
||||
e --> f
|
||||
```
|
||||
|
||||
Folgendes ist **kein** DAG:
|
||||
```mermaid
|
||||
flowchart LR
|
||||
a((A))
|
||||
b((B))
|
||||
c((C))
|
||||
d((D))
|
||||
e((E))
|
||||
f((F))
|
||||
a --> b
|
||||
b --> c
|
||||
d --> b
|
||||
c --> e
|
||||
e --> f
|
||||
e --> d
|
||||
```
|
||||
|
||||
## Äquivalenzklasse
|
||||
Eine Äquivalenzklasse beinhaltet alle Elemente, welche einer Klasse zugeordnet werden können
|
||||
|
||||

|
||||
|
||||
## Äquivalenzrelation
|
||||
|
||||
|
||||
# Themen
|
||||
- Chinesischer Restsatz
|
||||
- Euklidischer Algorithmus (ggt, kgv berechnen)
|
||||
|
||||

|
||||
|
||||
# Glossar
|
||||
| Bezeichnung | Beschreibung |
|
||||
| -------------------- | ------------------------------------------------------------------ |
|
||||
| Knotenmenge | Die Menge aller Elemente (Knoten), die in einem Graphen vorkommen. |
|
||||
| Wahrheits-Konstanten | $\top$ steht für `true`, $\bot$ für `false`.
|
||||
|
After 
(image error) Size: 48 KiB |
BIN
Notes/Semester 1/DM - Diskrete Mathematik/assets/SetDelta.png
Normal file
|
After 
(image error) Size: 49 KiB |
BIN
Notes/Semester 1/DM - Diskrete Mathematik/assets/SetExamples.png
Normal file
|
After 
(image error) Size: 14 KiB |
|
After 
(image error) Size: 53 KiB |
BIN
Notes/Semester 1/DM - Diskrete Mathematik/assets/SetMinus.png
Normal file
|
After 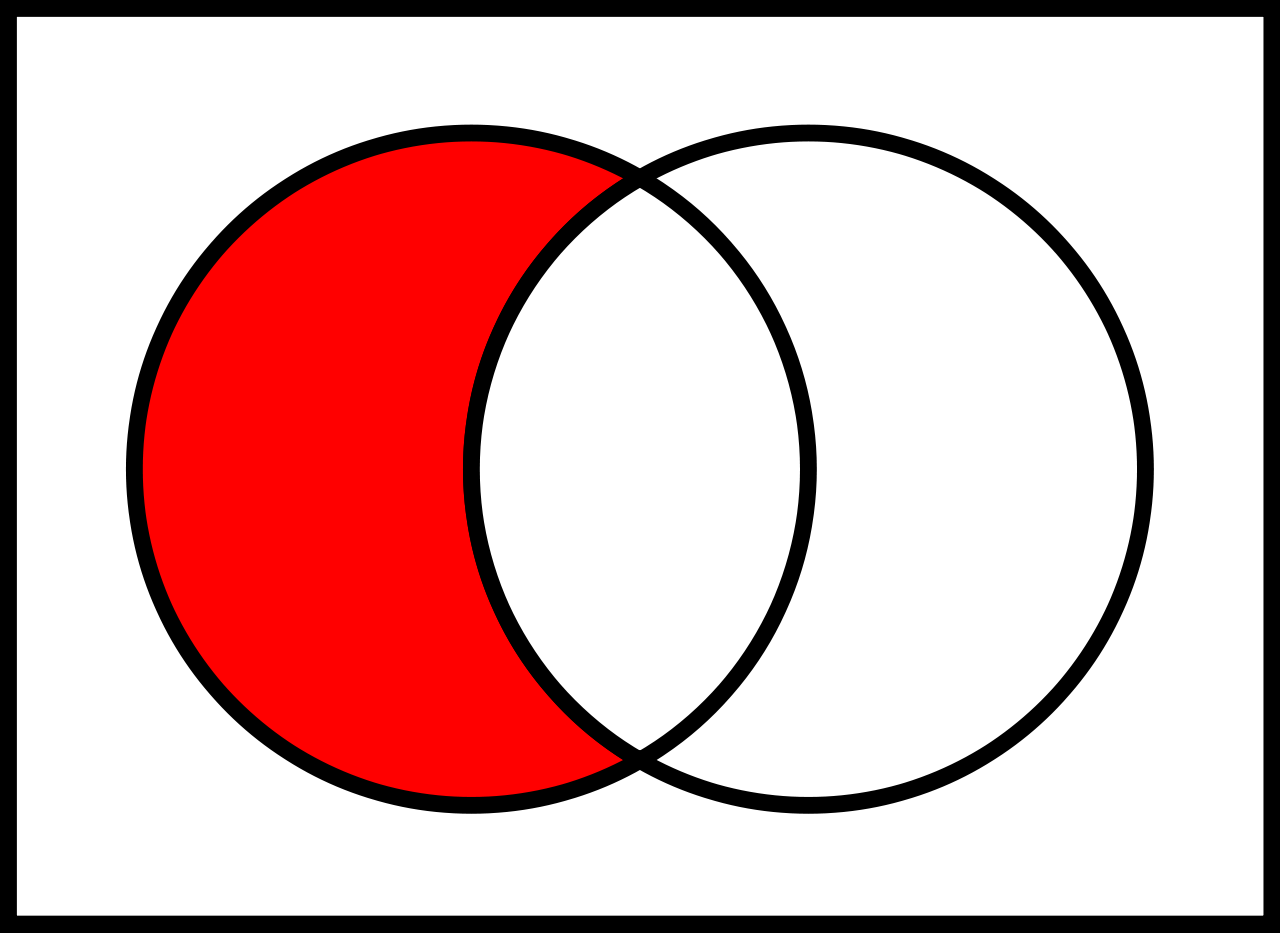
(image error) Size: 52 KiB |
BIN
Notes/Semester 1/DM - Diskrete Mathematik/assets/SetUnion.png
Normal file
|
After 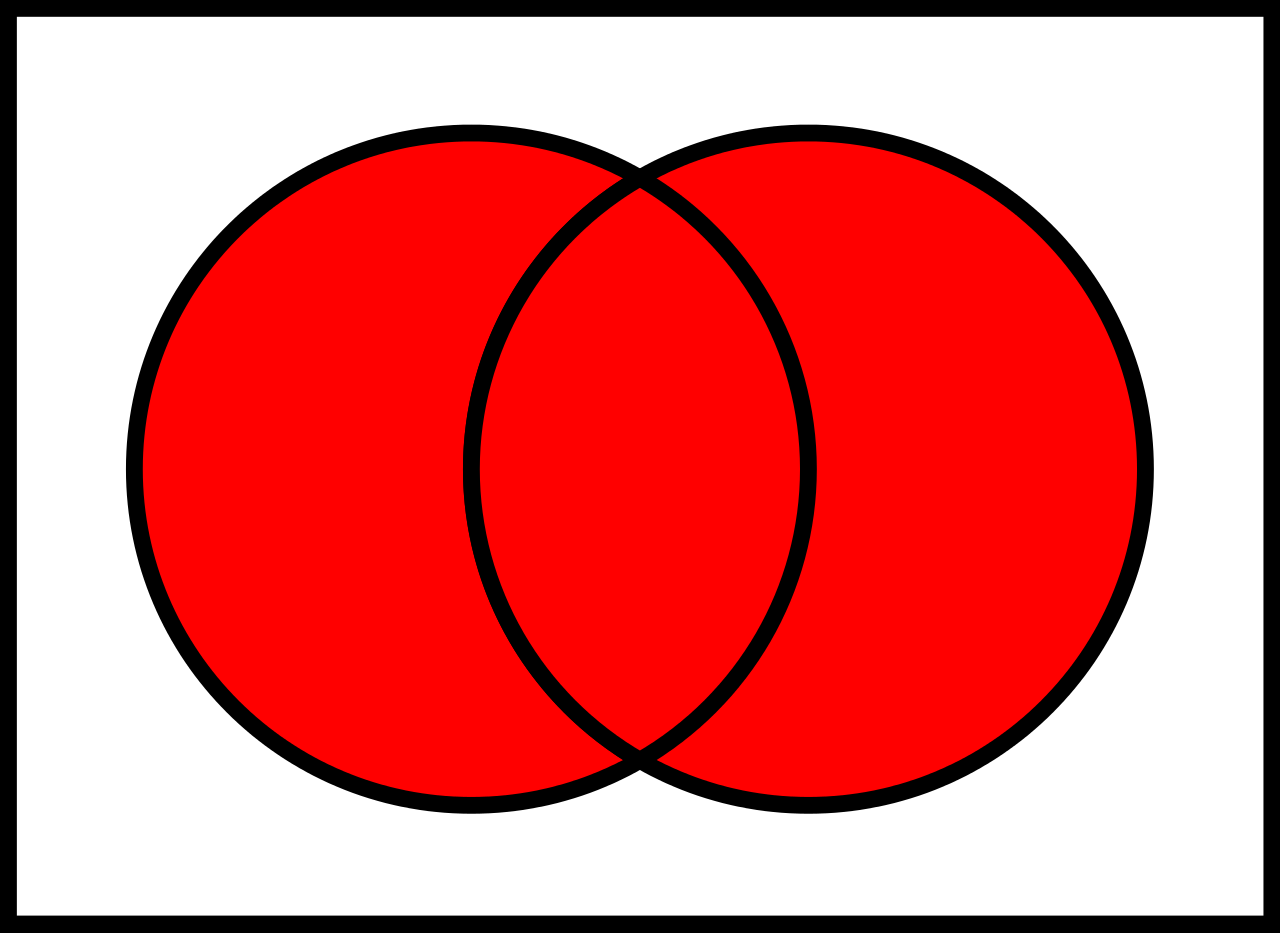
(image error) Size: 46 KiB |
BIN
Notes/Semester 1/DM - Diskrete Mathematik/assets/SortGraph.png
Normal file
|
After 
(image error) Size: 51 KiB |
|
After 
(image error) Size: 50 KiB |
|
|
@ -0,0 +1,16 @@
|
|||
# Gleichmässig Beschläunigte Bewegung
|
||||
Bewegung mit konstanter Beschläunigung
|
||||
|
||||
$$a = const.$$
|
||||
$$v(t) = v(0) + a * t$$
|
||||
$$a = \frac{\Delta v}{\Delta t}$$
|
||||
$$\int^{v(t)}_{v(0)} \Delta v = \int^t_0 a \Delta t$$
|
||||
$$v \int^{v(t)}_{v(0)} = v(t) - v(0) = a \times \int^t_0 = a \times (t - 0)$$
|
||||
$$\Rightarrow v(t) - v(0) = a \times t \Rightarrow v(t) = v(0) + a \times t$$
|
||||
$$v_x = \frac{\Delta x}{\Delta t}$$
|
||||
$$x(t) = x(0) + v(0) \times t + \frac{1}{2}at^2$$
|
||||
|
||||
Zeitfreie:
|
||||
$$x(t)-x(0) = \frac{v(t)^2 - v(0)^2}{2a}$$
|
||||
|
||||
(Script: Spezialfall $x = \frac{v^2}{2a}$, $x(0) = v(0) = 0$)
|
||||
|
|
@ -0,0 +1,17 @@
|
|||
# SI-Einheiten
|
||||
## Einheit Energie/Arbeit
|
||||
Die Einheit von Energie/Arbeit ist $J$ (Joule).
|
||||
|
||||
Energie:
|
||||
|
||||
$$1J=1N \times m=1kg \frac{m^2}{s^2}$$
|
||||
|
||||
Leistung
|
||||
|
||||
$$P=\frac{\Delta E}{\Delta t}$$
|
||||
|
||||
Einheit Leistung: $[P] = W$
|
||||
|
||||
$1W = 1 \frac{J}{s}$ => $1 Ws = 1J$
|
||||
|
||||
$$1kWh = 1 \times 10^3 W \times (3.6 \times 10^3s) = 3.6 \times 10^6 Ws = 3.6 \times 10^6J = 3.6 MJ$$
|
||||
|
|
@ -0,0 +1,10 @@
|
|||
# Stromkreis
|
||||
## Spannung
|
||||
Die Spannung beschreibt die Differenz zweier Ladungen. Die Spannung sorgt dafür, dass der Strom fliesst.
|
||||
|
||||
## Kondensator
|
||||
Q - Elektrische Ladung gemessen in $C$ (Coulomb => $A \cdot s$)
|
||||
|
||||
### Kapazität
|
||||
> **_Kapazität:_**
|
||||
> $$C = \frac{Q}{K_C}$$
|
||||
|
|
@ -0,0 +1 @@
|
|||
# Inhaltsverzeichnis
|
||||
|
|
@ -0,0 +1,23 @@
|
|||
# Zusammenfassung Physik
|
||||
## Knotenregel
|
||||
Summe aller Ströme ist 0
|
||||
|
||||
## Maschen-Regel
|
||||
Summe aller Spannungen ist 0
|
||||
|
||||
## Ohmsches Gesetz
|
||||
$$U = R \cdot I$$
|
||||
|
||||
## Schaltungsregeln
|
||||
### Serien-Schaltungen
|
||||
$$R_\text{total} = R_1 + R_2 + R_2 + R_3$$
|
||||
|
||||
### Parallel-Schaltung
|
||||
$$R_\text{total} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}} = \left(\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}\right)^{-1}$$
|
||||
|
||||
## Misc
|
||||
Unterschied Schwarzer Strahler und Schwarzer Körper:
|
||||
- Schwarzer Strahler ist dasselbe wie ein Schwarzer Körper
|
||||
Schwarze Körper absorbieren & emittieren alles - reflektieren aber nichts
|
||||
|
||||
Schwarze Strahler haben einen Emissionskoeffizient = 1, Graue Strahler haben einen Emissionskoeffizient < 1
|
||||
41
Notes/Semester 1/INCO - Informatik und Codierung/Gatter.md
Normal file
|
|
@ -0,0 +1,41 @@
|
|||
# Gatter
|
||||
Gatter sind Hardware (Transistoren), welche binäre Daten verarbeiten können. (Binäre: 0en und 1en)
|
||||
Diese werden üblicherweise als Boxen dargestellt.
|
||||
|
||||
## Rechenoperationen
|
||||
### `AND`
|
||||
```mermaid
|
||||
graph LR;
|
||||
a["A"];
|
||||
b["B"];
|
||||
out["C"];
|
||||
and["&"];
|
||||
a --- and;
|
||||
b --- and;
|
||||
and --- out;
|
||||
```
|
||||
|
||||
Ein `AND` (einige, verschiedene Notationen sind `AND`, `&` und $\wedge$) setzt voraus, dass die Eingabe-Werte (hier `A` und `B`) beide den Wert `true` beinhalten.
|
||||
|
||||
### NAND
|
||||
```mermaid
|
||||
graph LR;
|
||||
a["A"];
|
||||
b["B"];
|
||||
out["C"];
|
||||
and["&"];
|
||||
not((" "));
|
||||
a --- and;
|
||||
b --- and;
|
||||
and --- not --- out;
|
||||
```
|
||||
|
||||
Ein `NAND` (kurz für "not and") ist die invertierte Version der [`AND`-Operation](#and). Dieser setzt voraus, dass eine der Eingabe-Werte (hier `A` und `B`) **nicht** `true` entsprechen.
|
||||
|
||||
Ein `NAND` lässt sich folgendermassen umformen:
|
||||
$$C = \overline{A \wedge B}$$
|
||||
$$C = \overline{A} \vee \overline{B}$$
|
||||
|
||||
## Vereinfachung
|
||||
Für die Hardwaretechnik ist es jeweils effizienter, dieselben Operationen für alle Gatter zu verwenden.
|
||||
Dies ist bei einer Vereinfachung zu berücksichtigen.
|
||||
|
|
@ -0,0 +1,7 @@
|
|||
# Zusammenfassung
|
||||
## Zahlensysteme
|
||||
Zahlensysteme sind Arten, Zahlen darzustellen anhand deren Basis.
|
||||
|
||||
### Beispiel
|
||||
#### Dezimalsystem
|
||||
| $16
|
||||
0
Notes/Semester 1/INCO - Informatik und Codierung/JPEG.md
Normal file
|
|
@ -0,0 +1,9 @@
|
|||
# Kombinatorische Logik
|
||||
Die Kombinatorische Logik bezeichnet logische, binäre Operationen, deren Eingänge und Ausgänge beschreibt.
|
||||
Beschrieben werden lediglich simple Zustände ohne Speicherung von Daten.
|
||||
|
||||
Da kombinatorische Logiken Systeme ohne Speicher beschreiben, sind unter dieser Prämisse sind die Ergebnisse immer vorhersehbar (es sei denn, eine der Eingänge liefert zufällige Werte).
|
||||
|
||||
Kombinatorische Logik kann mit Hilfe sogenannter Gatter dargestellt werden.
|
||||
|
||||
Diese werden unter dem Punkt [Gatter](./Gatter.md) genauer erklärt:
|
||||
1
Notes/Semester 1/INCO - Informatik und Codierung/Q&A.md
Normal file
|
|
@ -0,0 +1 @@
|
|||
- Was ist die Aussage von H(ε)?
|
||||
|
|
@ -0,0 +1,23 @@
|
|||
# Quellencodierung
|
||||
## Ziel ist die Datenkompression
|
||||
* Speicherplatz sparen
|
||||
* Bandbreite reduzieren
|
||||
* => Kosten minimieren
|
||||
* Überarbeitungszeit reduzieren
|
||||
* Energie sparen
|
||||
* Optimierung zwischen Verarbeitung und Übertragung
|
||||
|
||||
## Keine Ziele der Quellencodierung sind
|
||||
* Datenverschlüsselung (Chiffrierung)
|
||||
|
||||
## Redundanz
|
||||
Falls Redundanz R grösser als 0 ist, kann verlustfrei komprimiert werden.
|
||||
Ist die Redundanz R kleiner als 0, so wird verlustbehaftet komprimiert.
|
||||
0 bedeutet keine Redundanz => keine Komprimierung
|
||||
< 0 bedeutet das "Wegwerfen" von Informationen (bspw. gewisse Frequenzen in .mp3)
|
||||
|
||||
## Huffman-Code
|
||||
|
||||
### Kompressions-Algorithmen
|
||||
#### LZ77
|
||||
|
||||
|
|
@ -0,0 +1,4 @@
|
|||
# Inhaltsverzeichnis
|
||||
- [Kombinatorische Logik](./Kombinatorische%20Logik.md)
|
||||
- [Gatter](./Gatter.md)
|
||||
- [Lektionen](./Lessons)
|
||||
|
|
@ -0,0 +1,39 @@
|
|||
# Zahlensysteme
|
||||
Zahlensysteme haben jeweils eine bestimme Basis, die darüber bestimmt, welche Wertigkeit die einzelnen Ziffern haben.
|
||||
|
||||
So hat unser herkömmliches System, das Dezimalsystem, die Basis 10. Die erste Ziffer hat den Wert $10^0$, die zweite Ziffer den Wert $10^1$, die dritte den Wert $10^2$ etc.
|
||||
|
||||
## Zahlensysteme umwandeln
|
||||
### Binärzahlen in Hexadezimal umwandeln
|
||||
Binär- und Hexadezimal-Zahlen lassen sich problemlos umwandeln.
|
||||
|
||||
Jede Hexadezimalzahl entspricht jeweils 4 Stellen im Binärsystem. Folgend eine Tabelle mit allen Hexadezimal-Zahlen und deren Binären Repräsentationen:
|
||||
|
||||
| Hex | Bin |
|
||||
| :---: | :----: |
|
||||
| $0$ | $0000$ |
|
||||
| $1$ | $0001$ |
|
||||
| $2$ | $0010$ |
|
||||
| $3$ | $0011$ |
|
||||
| $4$ | $0100$ |
|
||||
| $5$ | $0101$ |
|
||||
| $6$ | $0110$ |
|
||||
| $7$ | $0111$ |
|
||||
| $8$ | $1000$ |
|
||||
| $9$ | $1001$ |
|
||||
| $A$ | $1010$ |
|
||||
| $B$ | $1011$ |
|
||||
| $C$ | $1100$ |
|
||||
| $D$ | $1101$ |
|
||||
| $E$ | $1110$ |
|
||||
| $F$ | $1111$ |
|
||||
|
||||
> Beispiel anhand des $8$er- (Oktal)-Systems:
|
||||
> | $8^3$ | $8^2$ | $8^1$ | $8^0$ |
|
||||
> | :---: | :---: | :---: | :---: |
|
||||
> | $6$ | $2$ | $5$ | $7$ |
|
||||
>
|
||||
> $$6257_8 = \\
|
||||
> 6 \cdot 8^3 + 2 \cdot 8^2 + 5 \cdot 8^1 + 7 \cdot 8^0 = \\
|
||||
> 6 \cdot 512 + 2 \cdot 64 + 5 \cdot 8 + 7 \cdot 1 = \\
|
||||
> 3072 + 128 + 40 + 8 = 3248$$
|
||||
|
|
@ -0,0 +1,890 @@
|
|||
---
|
||||
Footer:
|
||||
Left: ""
|
||||
Right: ""
|
||||
Center: ""
|
||||
Header:
|
||||
Left: ""
|
||||
Right: ""
|
||||
Center: ""
|
||||
---
|
||||
<script src="../../../assets/deployggb.js"></script>
|
||||
<script src="../../../assets/graphs.js"></script>
|
||||
<script>
|
||||
window.graphs(
|
||||
[
|
||||
[
|
||||
"binEntropy",
|
||||
[
|
||||
"H_b(p) = p * log_2(1/p) + (1 - p) * log_2(1/(1 - p))",
|
||||
"SetCaption(H_b, \"H_b(p)\")",
|
||||
"a = IntegralBetween(H_b, 0, 0.0001, 0.9999)",
|
||||
"SetCaption(a, \"P(1)\")",
|
||||
"b = IntegralBetween(H_b, 1, 0.000001, 0.9999)",
|
||||
"SetCaption(b, \"P(0)\")"
|
||||
],
|
||||
undefined,
|
||||
(api) =>
|
||||
{
|
||||
api.evalCommand("ZoomIn(0.001, -0.2, 1, 1.1)");
|
||||
api.setColor("a", 0, 255, 0);
|
||||
api.setColor("b", 255, 0, 0);
|
||||
}
|
||||
]
|
||||
]);
|
||||
</script>
|
||||
|
||||
# Zusammenfassung INCO
|
||||
## Inhaltsverzeichnis
|
||||
- [Zusammenfassung INCO](#zusammenfassung-inco)
|
||||
- [Inhaltsverzeichnis](#inhaltsverzeichnis)
|
||||
- [Formeln](#formeln)
|
||||
- [Zahlensysteme](#zahlensysteme)
|
||||
- [Zahlen berechnen](#zahlen-berechnen)
|
||||
- [Hex $\Leftrightarrow$ Bin](#hex-leftrightarrow-bin)
|
||||
- [Rechen-Operationen](#rechen-operationen)
|
||||
- [Addition](#addition)
|
||||
- [Subtraktion](#subtraktion)
|
||||
- [Multiplikation](#multiplikation)
|
||||
- [Division](#division)
|
||||
- [Darstellung von Negativen Zahlen](#darstellung-von-negativen-zahlen)
|
||||
- [$1$er-Komplement](#1er-komplement)
|
||||
- [$2$er-Komplement](#2er-komplement)
|
||||
- [Informationstheorie](#informationstheorie)
|
||||
- [Formeln](#formeln-1)
|
||||
- [Probability $P(x)$](#probability-px)
|
||||
- [Informationsgehalt $I(x)$](#informationsgehalt-ix)
|
||||
- [Entropie $H(x)$](#entropie-hx)
|
||||
- [Quellencodierung](#quellencodierung)
|
||||
- [Grundsätze](#grundsätze)
|
||||
- [Übersicht](#übersicht)
|
||||
- [Formeln](#formeln-2)
|
||||
- [Mittlere Symbollänge $L(x)$](#mittlere-symbollänge-lx)
|
||||
- [Redundanz einer Codierung $R(x)$](#redundanz-einer-codierung-rx)
|
||||
- [Run Length Encoding `RLE`](#run-length-encoding-rle)
|
||||
- [Huffman Code](#huffman-code)
|
||||
- [LZ77-Kompression](#lz77-kompression)
|
||||
- [LZW-Kompression](#lzw-kompression)
|
||||
- [JPEG-Kompressionsverfahren](#jpeg-kompressionsverfahren)
|
||||
- [Aufteilung in Luminanz und Chrominanz](#aufteilung-in-luminanz-und-chrominanz)
|
||||
- [Downsampling](#downsampling)
|
||||
- [Block-Verarbeitung](#block-verarbeitung)
|
||||
- [Diskrete Kosinus Transformation](#diskrete-kosinus-transformation)
|
||||
- [Quantisierung](#quantisierung)
|
||||
- [Entropy Encoding](#entropy-encoding)
|
||||
- [Qualitätsunterschied](#qualitätsunterschied)
|
||||
- [Audiocodierung](#audiocodierung)
|
||||
- [Abtasttheorem](#abtasttheorem)
|
||||
- [Quantisierung](#quantisierung-1)
|
||||
- [Kanalcodierung](#kanalcodierung)
|
||||
- [Fehlerkorrekturverfahren](#fehlerkorrekturverfahren)
|
||||
- [Backward Error Correction](#backward-error-correction)
|
||||
- [Forward Error Correction](#forward-error-correction)
|
||||
- [Binäre Kanäle](#binäre-kanäle)
|
||||
- [Bitfehlerwahrscheinlichkeit](#bitfehlerwahrscheinlichkeit)
|
||||
- [Binary Symmetric Channel](#binary-symmetric-channel)
|
||||
- [Mehrbitfehlerwahrscheinlichkeit Berechnen](#mehrbitfehlerwahrscheinlichkeit-berechnen)
|
||||
- [Wahrscheinlichkeiten in einem BSC](#wahrscheinlichkeiten-in-einem-bsc)
|
||||
- [Binäre Kanalcodes](#binäre-kanalcodes)
|
||||
- [Code-Rate](#code-rate)
|
||||
- [Hamming-Distanz](#hamming-distanz)
|
||||
- [Beispiele](#beispiele)
|
||||
- [Hamming Distanz 1](#hamming-distanz-1)
|
||||
- [Hamming Distanz 2](#hamming-distanz-2)
|
||||
- [Hamming Distanz 3](#hamming-distanz-3)
|
||||
- [Hamming-Gewicht](#hamming-gewicht)
|
||||
- [Eigenschaften von Binären Kanalcodes](#eigenschaften-von-binären-kanalcodes)
|
||||
- [Perfekt](#perfekt)
|
||||
- [Systematisch](#systematisch)
|
||||
- [Linear](#linear)
|
||||
- [Zyklisch](#zyklisch)
|
||||
- [Fehlererkennung](#fehlererkennung)
|
||||
- [Paritäts-Check](#paritäts-check)
|
||||
- [Cyclic Redundancy Check CRC](#cyclic-redundancy-check-crc)
|
||||
- [Fehlerkorrektur](#fehlerkorrektur)
|
||||
- [Lineare Block-Codes](#lineare-block-codes)
|
||||
- [Faltungscode](#faltungscode)
|
||||
- [Schaltungs-Umsetzung eines Faltungscodes](#schaltungs-umsetzung-eines-faltungscodes)
|
||||
- [Glossar](#glossar)
|
||||
|
||||
## Formeln
|
||||
|
||||
|
||||
## Zahlensysteme
|
||||
### Zahlen berechnen
|
||||
> Beispiel anhand des $8$er- (Oktal)-Systems:
|
||||
> | $8^3$ | $8^2$ | $8^1$ | $8^0$ |
|
||||
> | :---: | :---: | :---: | :---: |
|
||||
> | $6$ | $2$ | $5$ | $7$ |
|
||||
>
|
||||
> $$6257_8 =$$
|
||||
> $$6 \cdot 8^3 + 2 \cdot 8^2 + 5 \cdot 8^1 + 7 \cdot 8^0 =$$
|
||||
> $$6 \cdot 512 + 2 \cdot 64 + 5 \cdot 8 + 7 \cdot 1 =$$
|
||||
> $$3072 + 128 + 40 + 8 = 3248$$
|
||||
|
||||
### Hex $\Leftrightarrow$ Bin
|
||||
| Hex | Bin |
|
||||
| :---: | :----: |
|
||||
| $0$ | $0000$ |
|
||||
| $1$ | $0001$ |
|
||||
| $2$ | $0010$ |
|
||||
| $3$ | $0011$ |
|
||||
| $4$ | $0100$ |
|
||||
| $5$ | $0101$ |
|
||||
| $6$ | $0110$ |
|
||||
| $7$ | $0111$ |
|
||||
| $8$ | $1000$ |
|
||||
| $9$ | $1001$ |
|
||||
| $A$ | $1010$ |
|
||||
| $B$ | $1011$ |
|
||||
| $C$ | $1100$ |
|
||||
| $D$ | $1101$ |
|
||||
| $E$ | $1110$ |
|
||||
| $F$ | $1111$ |
|
||||
|
||||
### Rechen-Operationen
|
||||
Operationen werden generell identisch zu den herkömmlichen schriftlichen Rechenoperationen durchgeführt.
|
||||
|
||||
#### Addition
|
||||

|
||||
|
||||
#### Subtraktion
|
||||

|
||||
|
||||
#### Multiplikation
|
||||

|
||||
|
||||
#### Division
|
||||

|
||||
|
||||
### Darstellung von Negativen Zahlen
|
||||
#### $1$er-Komplement
|
||||
Das $1$er-Komplement wird gebildet indem man jede Ziffer einer Zahl durch die Ergänzung auf $1$ ersetzt:
|
||||
| Ursprüngliche Zahl | $0010$ |
|
||||
| ------------------ | ------ |
|
||||
| Subtrahend | $1111$ |
|
||||
| $1$er-Komplement | $1101$ |
|
||||
|
||||
Genauso kann für Dezimal-Zahlen ein $9$er-Komplement gebildet werden, indem alle Ziffern mit der Ergänzung auf $9$ ersetzt werden:
|
||||

|
||||
|
||||
Das Problem des $1$er-Komplements ist, dass $0$ zwei verschiedene Darstellungsweisen hat.
|
||||
|
||||
Das $1$er-Komplement von $0$ lautet nämlich folgendermassen:
|
||||
|
||||
| Ursprüngliche Zahl | $0000$ |
|
||||
| ------------------ | ------ |
|
||||
| Subtrahend | $1111$ |
|
||||
| $1$er-Komplement | $1111$ |
|
||||
|
||||
Die $0$ kann also mit dem $1$er-Komplement sowohl als $0000$ als auch als $1111$ dargestellt werden.
|
||||
|
||||
#### $2$er-Komplement
|
||||
Das $2$er-Komplement schafft hierbei Abhilfe und wird gebildet, indem man das $1$er-Komplement um $1$ erhöht:
|
||||
|
||||
| Ursprüngliche Zahl | $0010$ |
|
||||
| ------------------ | ------ |
|
||||
| Subtrahend | $1111$ |
|
||||
| $1$er-Komplement | $1101$ |
|
||||
| Summand | $0001$ |
|
||||
| $2$er-Komplement | $1110$ |
|
||||
|
||||
So ergibt die Bildung des Komplements von $0$ folgendes:
|
||||
|
||||
| Ursprüngliche Zahl | $0000$ |
|
||||
| ------------------ | ------ |
|
||||
| Subtrahend | $1111$ |
|
||||
| $1$er-Komplement | $1111$ |
|
||||
| Summand | $0001$ |
|
||||
| $2$er-Komplement | $0000$ |
|
||||
|
||||
## Informationstheorie
|
||||

|
||||
|
||||
### Formeln
|
||||
#### Probability $P(x)$
|
||||
Die Wahrscheinlichkeit errechnet sich indem man die Anzahl Vorkommen des Symbols ($N_x$) durch die gesamte Anzahl Symbole in der Nachricht ($N$) teilt:
|
||||
$$P(x) = \frac{N_x}{N}$$
|
||||
|
||||
> **Beispiel:**
|
||||
> Für ein Symbol, das $2$-mal in einer Nachricht mit $4$ Symbolen vorkommt, würde die Rechnung also folgendermassen aussehen:
|
||||
> $$P(x) = \frac{N_x}{N} = \frac{2}{4} = \frac{1}{2} = 0.5$$
|
||||
|
||||
#### Informationsgehalt $I(x)$
|
||||
Der Informationsgehalt errechnet sich, indem man berechnet, wieviele Bits mindestens benötigt werden, um das Symbol $x$ darzustellen.
|
||||
Je weniger man ein Symbol in einer Nachricht erwartet, desto höher ist dessen Informationsgehalt.
|
||||
|
||||
$$I(x) = \log_2\left(\frac{1}{P(x)}\right)$$
|
||||
|
||||
#### Entropie $H(x)$
|
||||
Die Entropie besagt, was der durchschnittliche Informationsgehalt einer Datenquelle ist.
|
||||
|
||||
Die Entropie eines einzelnen Symbols oder eines einzelnen Falls errechnet sich wie folgt:
|
||||
|
||||
$$H(x) = P(x) \cdot \log_2\left(\frac{1}{P(x)}\right)$$
|
||||
|
||||
Folgendermassen errechnet sich die Entropie einer ganzen Datenquelle:
|
||||
|
||||
$$H(x) = \sum^{N-1}_{n=1}\left(P(x_n) \cdot \log_2\left(\frac{1}{P(x_n)}\right)\right)$$
|
||||
|
||||
Je gleichmässiger die Häufigkeit der einzelnen Symbole, desto höher die Entropie.
|
||||
|
||||
Die untenstehende Grafik zeigt das Verhältnis zwischen der Wahrscheinlichkeit in einem BMS (Binary Memoryless Source) und der daraus resultierenden Entropie.
|
||||
|
||||
<div id="binEntropy"></div>
|
||||
|
||||
Wie zu sehen ist die Entropie am höchsten, wenn die Wahrscheinlichkeit für $1$en ($P(1)$) identisch mit der Wahrscheinlichkeit für $0$en ($P(0)$) ist.
|
||||
|
||||
## Quellencodierung
|
||||
Unter Quellencodierung versteht man die Aufbereitung von Daten für einen optimierten Versand.
|
||||
|
||||
### Grundsätze
|
||||
Die Grundsätze und/oder Ziele der Quellencodierung sind folgende:
|
||||
|
||||
- Speicherplatz sparen
|
||||
- Bandbreite reduzieren
|
||||
- Kosten minimieren
|
||||
- Übertragungszeit reduzieren
|
||||
- Energie sparen
|
||||
- Optimierung zwischen Verarbeitung und Übertragung
|
||||
|
||||
Folgendes sind **keine** Ziele der Quellencodierung
|
||||
|
||||
- ~~_Datenverschlüsselung (Chiffrierung, Security)_~~
|
||||
- ~~_Sicherung der Datenintegrität durch Fehlererkennung und Fehlerkorrektur (folgt später, siehe Kanalcodierung)_~~
|
||||
|
||||
### Übersicht
|
||||

|
||||
|
||||
- Die **Irrelevanz**-Reduktion ist darauf ausgelegt, Daten zu entfernen, die für den Empfänger irrelevant sind
|
||||
- Nicht-hörbare Frequenzen bspw. in Musik
|
||||
- Überhöhte, nicht wahrnehmbare Bildwiederholfrequenz
|
||||
- Nicht wahrnehmbare Farben in Bildern
|
||||
- Die Reduktion von **Redundanz** beschreibt die das **verlustfreie** Komprimieren von Daten
|
||||
|
||||
### Formeln
|
||||
#### Mittlere Symbollänge $L(x)$
|
||||
$$L(x) = \sum_{n=0}^{N - 1} P(x_n) \cdot l_n$$
|
||||
|
||||
_Einheit: $\frac{Bit}{Symbol}$_
|
||||
|
||||
#### Redundanz einer Codierung $R(x)$
|
||||
$$R(x) = L(x) - H(x)$$
|
||||
|
||||
_Einheit: $\frac{Bit}{Symbol}$_
|
||||
|
||||
Falls die Entropie einer Datenquelle grösser ist als die durchschnittliche Länge der codierten Worte, handelt es sich bei der Codierung um eine verlustbehaftete Kompression.
|
||||
|
||||
### Run Length Encoding `RLE`
|
||||
Die Lauflängencodierung ist die simpelste Art von Komprimierung.
|
||||
Diese basiert auf das Prinzip, sich wiederholende Frequenzen in der Form `[Marker, Anzahl, Symbol]` festzuhalten.
|
||||
|
||||
Die Anzahl Bits, welche für da Speichern der `Anzahl` aufgewendet werden, sollte so gewählt werden, dass die typische Länge von `RLE`-Blöcken abgebildet werden kann.
|
||||
|
||||
Tritt also ein Symbol sehr oft hintereinander auf: `ABBBBBBBBBA`
|
||||
|
||||
Könnte diese beispielsweise in der folgenden Form dargestellt werden: `AC9BA`
|
||||
|
||||
`C` wird an dieser Stelle als `RLE`-Marker (Segment, welche den Start eines `RLE`-Codes markiert) eingesetzt.
|
||||
|
||||
> ***Beispiel:***
|
||||
> In diesem Code wird von einem System ausgegangen, welches nur die Übertragung von `T`, `E`, `R`, `A`, `U`, `I`, `W`, `Q`, `C`, `S` und `L` zulässt.
|
||||
> - Quelle:
|
||||
> `TERRRRRRRRRMAUIIIIIIIIIIIIIIIIIWQCSSSSSSSSSSL`
|
||||
>
|
||||
> Als `RLE`-Marker sollte das Symbol verwendet werden, das am allerwenigsten vorkommt (in diesem Fall wäre das `A`).
|
||||
> Da sich in der Quelle Symbole teils 10-17 Mal wiederholen werden für das Speichern der `Anzahl` 2 Dezimalstellen (oder 5 Bits) verwendet:
|
||||
> - `RLE`-komprimiert:
|
||||
> `TE`<span style="text-decoration: underline">***`A09R`***</span>`M`<span style="text-decoration: underline">***`A01A`***</span>`U`<span style="text-decoration: underline">***`A17I`***</span>`WQC`<span style="text-decoration: underline">***`A10S`***</span>`L`
|
||||
|
||||
### Huffman Code
|
||||
Der Huffman Code ermöglicht es einem, Codeworte zu generieren, welche folgende wichtige Grundsätze einhalten:
|
||||
- Häufige Symbole haben kurze Code-Worte
|
||||
- Seltene Symbole haben lange Code-Worte
|
||||
- Präfix-frei
|
||||
- Optimal (kein besserer, Präfix-freier Code möglich)
|
||||
|
||||
Schritte zum Bilden eines Huffman-Codes
|
||||
1. Alle Symbole aufsteigend nach Wahrscheinlichkeit $P(x)$ auflisten - dies sind die _Blätter_ des Huffman-Baums
|
||||
2. Entsprechende Wahrscheinlichkeiten dazuschreiben
|
||||
3. Blätter mit der kleinsten Wahrscheinlichkeit verbinden und die Summe der Wahrscheinlichkeiten in der entstehenden Gabelung notieren
|
||||
4. Punkt 3 Wiederholen bis alle Blätter miteinander verbunden sind
|
||||
5. Festlegen, welche Richtung des Astes einer Gabelung einer $0$ oder einer $1$ entspricht
|
||||
6. Entstehende Code-Werte notieren
|
||||
|
||||
> ***Beispiel:***
|
||||
> Beispiel anhand von `M`, `N`, `O`, `R`, `S` mit folgenden Wahrscheinlichkeiten:
|
||||
> $P(M) = 0.35$, $P(N) = 0.2$, $P(O) = 0.25$, $P(R) = 0.05$, $P(S) = 0.15$
|
||||
> ```mermaid
|
||||
> flowchart LR
|
||||
> r["R (111)"]---4((0.05))
|
||||
> s["S (110)"]---5((0.15))
|
||||
> n["N (10)"]---1((0.2))
|
||||
> p["O (01)"]---2((0.25))
|
||||
> m["M (00)"]---3((0.35))
|
||||
> a1((0.2))
|
||||
> 4---a1
|
||||
> 5---a1
|
||||
> b1((0.4))
|
||||
> a1---b1
|
||||
> 1---b1
|
||||
> a2((0.6))
|
||||
> 2---a2
|
||||
> 3---a2
|
||||
> c1((1.0))
|
||||
> b1---c1
|
||||
> a2---c1
|
||||
> ```
|
||||
> In diesem Beispiel wird die Richtungszuweisung $\uparrow = 1$ und $\downarrow = 0$ verwendet.
|
||||
|
||||
### LZ77-Kompression
|
||||
Im LZ77-Verfahren werden die Daten durch ein Sliding Window bestehend aus Such- und Vorschau-Buffer geleitet, um diese nach Gemeinsamkeiten abzutasten:
|
||||

|
||||
|
||||
Wie in der Abbildung zu sehen wird der Vorschau-Buffer nach Übereinstimmungen im Such-Buffer geprüft.
|
||||
|
||||
Folgend ein Beispiel des Vorgangs einer `LZ77`-Kompression mit der Eingabe `AMAMMMAAAMMMTAAT` mit einer Such-Buffer Länge von $8$ und einer Vorschau-Buffer Länge von $5$:
|
||||
|
||||
| Such-Buffer | Vorschau-Buffer | Input-Daten | Token (Offset, Länge, Zeichen) |
|
||||
| ----------- | --------------- | ------------- | ------------------------------ |
|
||||
| | `AMAMM` | `MAAAMMMTAAT` | `(0, 0, A)` |
|
||||
| `A` | `MAMMM` | `AAAMMMTAAT` | `(0, 0, M)` |
|
||||
| `AM` | `AMMMA` | `AAMMMTAAT` | `(2, 2, M)` |
|
||||
| `AMAMM` | `MAAAM` | `MMTAAT` | `(4, 2, A)` |
|
||||
| `AMAMMMAA` | `AMMMT` | `AAT` | `(6, 4, T)` |
|
||||
| `MMAAAMMT` | `AAT` | | `(6, 2, T)` |
|
||||
|
||||
Bei der Decodierung werden die Token interpretiert und dessen Resultat am Ende des Buffers hinzugefügt.
|
||||
So werden redundante Daten automatisch wiederhergestellt.
|
||||
|
||||
| Token | Resultierender Buffer |
|
||||
| ----------- | --------------------- |
|
||||
| `(0, 0, A)` | `A` |
|
||||
| `(0, 0, M)` | `AM` |
|
||||
| `(2, 2, M)` | `AMAMM` |
|
||||
| `(4, 2, A)` | `AMAMMMAA` |
|
||||
| `(6, 4, T)` | `AMAMMMAAAMMMT` |
|
||||
| `(6, 2, T)` | `AMAMMMAAAMMMTAAT` |
|
||||
|
||||
### LZW-Kompression
|
||||
Das LZW-Verfahren lehnt nur geringfügig an dem LZ77-Verfahren an. An Stelle eines Sliding-Windows wird ein Wörterbuch verwendet.
|
||||
|
||||
Das Wörterbuch hat zu Beginn des Kompression lediglich 255 Einträge mit den dazugehörigen ASCII-Charakteren.
|
||||
|
||||
Während der Kompression wird das Wörterbuch nach und nach aufgebaut, neue Wörterbuch-Einträge werden als Token versendet. Ein Token besteht aus dem Index eines übereinstimmenden Wörterbuch-Eintrags, welches möglichst viele Zeichen lang ist.
|
||||
|
||||
Der Wert des Tokens setzt sich aus dem Wert des verwiesenen Wörterbuch-Eintrags und dem ersten Zeichen des Werts des nächsten Tokens zusammen:
|
||||
|
||||

|
||||
|
||||
Folgend ein Beispiel anhand des zu komprimierenden Wertes: `AMAMMMAAAMMMTAAT`:
|
||||
|
||||
| Input-Daten | Token-Index | Token | Wert |
|
||||
| ------------------ | ----------- | ----- | ------ |
|
||||
| `AMAMMMAAAMMMTAAT` | `256` | `65` | `AM` |
|
||||
| `MAMMMAAAMMMTAAT` | `257` | `77` | `MA` |
|
||||
| `AMMMAAAMMMTAAT` | `258` | `256` | `AMM` |
|
||||
| `MMAAAMMMTAAT` | `259` | `77` | `MM` |
|
||||
| `MAAAMMMTAAT` | `260` | `257` | `MAA` |
|
||||
| `AAMMMTAAT` | `261` | `65` | `AA` |
|
||||
| `AMMMTAAT` | `262` | `258` | `AMMM` |
|
||||
| `MTAAT` | `263` | `77` | `MT` |
|
||||
| `TAAT` | `264` | `84` | `TA` |
|
||||
| `AAT` | `265` | `261` | `AAT` |
|
||||
| `T` | `266` | `84` | `T` |
|
||||
|
||||
Gesendet werden also folgende Daten:
|
||||
|
||||
```
|
||||
[65, 77, 256, 77, 257, 65, 258, 77, 84, 261, 84]
|
||||
```
|
||||
|
||||
> ***Hinweis:***
|
||||
> $65$ ist der ASCII-Wert von einem `A`, $77$ entspricht einem `M` und $84$ einem `T`.
|
||||
|
||||
Für die Decodierung werden die versendeten Wörterbuch-Einträge wieder zu eigentlichem Text umgewandelt:
|
||||
|
||||
| Index | Token | Wert | Resultierender Buffer |
|
||||
| ----- | ----- | ------ | --------------------- |
|
||||
| `256` | `65` | `A?` | `A` |
|
||||
| `257` | `77` | `M?` | `AM` |
|
||||
| `258` | `256` | `AM?` | `AMAM` |
|
||||
| `259` | `77` | `M?` | `AMAMM` |
|
||||
| `260` | `257` | `MA` | `AMAMMMA` |
|
||||
| `261` | `65` | `A?` | `AMAMMMAA` |
|
||||
| `262` | `258` | `AMM?` | `AMAMMMAAAMM` |
|
||||
| `263` | `77` | `M?` | `AMAMMMAAAMMM` |
|
||||
| `264` | `84` | `T?` | `AMAMMMAAAMMMT` |
|
||||
| `265` | `261` | `AA?` | `AMAMMMAAAMMMTAA` |
|
||||
| `266` | `84` | `T` | `AMAMMMAAAMMMTAAT` |
|
||||
|
||||
### JPEG-Kompressionsverfahren
|
||||
JPEG ist eine **verlustbehaftete** Kompressionsart. Es gibt auch die Möglichkeit, Bilder verlustfrei mit JPEG zu komprimieren, diese Möglichkeit ist aber in kaum einem Programm vorzufinden.
|
||||
Diese entfernt sowohl Redundanz als auch Bild-Informationen (Farben), welche für das menschliche Auge kaum ersichtlich sind.
|
||||
|
||||
JPEG eignet sich vor allem bei Fotografien, während es für Dokumente oder Computergrafiken (aka. Bilder mit scharfen Kanten wie Schriften oder Website-Banner) **nicht** geeignet ist.
|
||||
|
||||
#### Aufteilung in Luminanz und Chrominanz
|
||||
In einem ersten Schritt werden die Farbinformationen aufgeteilt in Luminanz $Y$, Chrominanz (Rot) $C_R$ und Chrominanz (Blau) $C_B$.
|
||||
Dieser Schritt ist notwendig, da das menschliche Auge viel affiner auf Helligkeit (die Luminanz) als auf Farben ist.
|
||||
|
||||
Der Schritt der Umwandlung von `RGB` in LCrCb ist verlustfrei.
|
||||
|
||||
Folgende Abbildung zeigt diese Umwandlung:
|
||||
|
||||

|
||||
|
||||
Die folgende Abbildung zeigt auf, wie die Farbwerte eines Bildes zu Luminanz-Werten umgerechnet werden können:
|
||||
|
||||

|
||||
|
||||
Mit Hilfe folgender Formel können aus `RGB`-Werten die dazugehörigen Luminanz und Chrominanz-Werte berechnet werden:
|
||||
|
||||
$$\begin{bmatrix}
|
||||
Y \\
|
||||
C_B \\
|
||||
C_R
|
||||
\end{bmatrix} =
|
||||
\begin{bmatrix}
|
||||
0.299 & 0.587 & 0.114 \\
|
||||
-0.1687 & -0.3313 & 0.5 \\
|
||||
0.5 & -0.4187 & -0.0813
|
||||
\end{bmatrix}
|
||||
\cdot
|
||||
\begin{bmatrix}
|
||||
R \\
|
||||
G \\
|
||||
B
|
||||
\end{bmatrix}
|
||||
+
|
||||
\begin{bmatrix}
|
||||
0 \\
|
||||
128 \\
|
||||
128
|
||||
\end{bmatrix}$$
|
||||
|
||||
> **Erinnerung:**
|
||||
> Im einzelnen bedeutet das bspw. folgendes:
|
||||
>
|
||||
> $$Y = (0.299 \cdot R + 0.587 \cdot G + 0.114 \cdot 0.114) + 0$$
|
||||
> $$C_B = (-0.1687 \cdot R + -0.3313 \cdot G + 0.5 \cdot B) + 128$$
|
||||
> $$C_R = (0.5 \cdot R + -0.4187 \cdot G + -0.0813 \cdot B) + 128$$
|
||||
|
||||
Die Formel zum Umwandeln von Luminanz- und Chrominanz-Werten lautet wie folgt:
|
||||
|
||||
$$\begin{bmatrix}
|
||||
R \\
|
||||
G \\
|
||||
B
|
||||
\end{bmatrix} =
|
||||
\begin{bmatrix}
|
||||
1 & 0 & 1.402 \\
|
||||
1 & -0.34414 & -0.71414 \\
|
||||
1 & 1.772 & 0
|
||||
\end{bmatrix}
|
||||
\cdot
|
||||
\begin{bmatrix}
|
||||
Y \\
|
||||
C_B - 128 \\
|
||||
C_R - 128
|
||||
\end{bmatrix}$$
|
||||
|
||||
#### Downsampling
|
||||
Da, wie bereits erwähnt, das Auge sensitiver auf Helligkeit (Luminanz) als auf Farben (Chrominanz) ist, kann die Auflösung der Chrominanz-Werte beliebig verringert werden.
|
||||
|
||||
Das Downsampling wird im Format `J:a:b` definiert.
|
||||
- `J` steht für die Breite der 2px hohen Blöcke
|
||||
- `a` steht für die Anzahl Pixel nach dem Down-Sampling in der 1. Zeile
|
||||
- `b` steht für die Anzahl Pixel nach dem Down-Sampling in der 2. Zeile
|
||||
|
||||

|
||||
|
||||
Folgend einige Beispiele:
|
||||
|
||||

|
||||
|
||||
Nach dem Downsampling sehen die Bilder jeweils folgendermassen aus:
|
||||
|
||||

|
||||
|
||||
#### Block-Verarbeitung
|
||||
Die hier geschilderten Schritte werden jeweils für Blöcke à 8x8 Pixel angewendet.
|
||||
Folgend ein Überblick über die einzelnen Schritte:
|
||||
|
||||

|
||||
|
||||
##### Diskrete Kosinus Transformation
|
||||
|
||||
Bei der Transformation werden die Werte in den 8x8-Blöcken (Werte von $0$ bis $254$) umgewandelt, sodass sie nicht mehr Koordinaten und die dazugehörigen Werte repräsentieren, sondern eine Gewichtung, wie sehr sie aus dem Muster einer bestimmten Kosinus-Frequenz zusammengesetzt sind:
|
||||
|
||||

|
||||
|
||||
Dies geschieht mit Hilfe folgender Formel:
|
||||
$$F_{vu} = \frac{1}{4} \cdot C_u \cdot C_v \cdot \sum_{x=0}^7\sum_{y=0}^7B_{xy} \cdot \cos\left(\frac{(2x + 1) \cdot u \cdot \pi}{16}\right) \cdot \cos\left(\frac{(2y + 1) \cdot v \cdot \pi}{16}\right)$$
|
||||
|
||||
> ***Information***:
|
||||
> $C_u,C_v = \frac{1}{\sqrt{2}}$ für $u=0$ oder $v=0$
|
||||
> $C_u,C_v = 1$ für alle anderen Fälle (i.e. $u \not =0$ und $v \not = 0$)
|
||||
|
||||
Folgendermassen lässt sich diese Formel auch wieder umkehren:
|
||||
$$B_{yx} = \frac{1}{4}\sum_{u=0}^7\sum_{v=0}^7 C_u \cdot C_v \cdot F_{vu} \cdot \cos\left(\frac{(2x + 1) \cdot u \cdot \pi}{16}\right) \cdot \cos\left(\frac{(2y + 1) \cdot v \cdot \pi}{16}\right)$$
|
||||
|
||||
##### Quantisierung
|
||||
Die gewonnene 8x8 Frequenz-Tabellen werden anschliessend quantisiert. In diesem Schritt werden aufgrund einer Quantisierungstabelle (welche Resultat intensiver Experimente war) alle Werte dividiert.
|
||||
|
||||
Dies führt dazu, dass vorwiegend nur signifikante Werte in der rechten oberen Ecke übrig bleiben:
|
||||
|
||||

|
||||
|
||||
##### Entropy Encoding
|
||||
In einem letzten Schritt werden der DC-Koeffizient (Wert ganz oben links) und die AC-Koeffizienten (alle übrigen Werte) mit Hilfe von Run Length Encoding (siehe [RLE](#run-length-encoding-rle)) in der Form `[DC-Wert, [Anzahl Nullen, Koeffizient]*, EOB]` gespeichert.
|
||||
|
||||
Der "End of Block" (`EOB`) Marker markiert hierbei die Stelle ab der nur noch $0$-Werte folgen. Die Werte werden in einer diagonalen "Zick-Zack" Form abgetastet:
|
||||
|
||||

|
||||
|
||||
> ***Beispiel:***
|
||||
> 
|
||||
>
|
||||
> Die in dieser Abbildung ersichtlichen Werte würden also folgendermassen codiert werden:
|
||||
>
|
||||
> ```
|
||||
> (79), (1, -2), (0, -1), (0, -1), (2, -1), (0, -1), (EOB)
|
||||
> ```
|
||||
|
||||
#### Qualitätsunterschied
|
||||
Folgendes Beispiel zeigt, wie sich JPEG-Bilder je nach gewählter Qualität unterscheiden.
|
||||
|
||||

|
||||
|
||||
## Audiocodierung
|
||||
Im Folgenden ist beschrieben, wie die Audiocodierung im Wave-Format funktioniert.
|
||||
|
||||
### Abtasttheorem
|
||||
Um ein Audiosignal korrekt abtasten zu können, muss die Abtast-Frequenz mindestens doppelt so gross sein wie die maximale Frequenz des Audio-Signals:
|
||||
|
||||
$$F_\text{abtast} > 2 \cdot F_\text{max}$$
|
||||
|
||||
Wird dieses Theorem nicht eingehalten, so kann es bspw. zu einer sog. "Spiegelung" kommen.
|
||||
|
||||
In diesem Fall führt, wie in der Abbildung zu sehen, das originale Signal (gelb hinterlegt) zu einem falschen Ausgabesignal (blau hinterlegt):
|
||||
|
||||

|
||||
|
||||
### Quantisierung
|
||||
Im Rahmen der Quantisierung wird versucht, mit Hilfe von Quantisierung das Signal so genau wie möglich in binärer Form abzubilden:
|
||||
|
||||

|
||||
|
||||
Da das quantisierte Signal nicht zu 100% dem originalen Signal entspricht entsteht jeweils ein Rauschen, welches pro zusätzlichem Bit, welches für das Quantisieren verwendet wird, um 6db abnimmt:
|
||||
|
||||

|
||||
|
||||
Im Vergleich: In der Telefonie wird eine Quantisierung mit 8 Bit vorgenommen - auf Audio-CDs mit 16 Bit. Aus diesem Grund klingen Anrufe sehr "verrauscht".
|
||||
|
||||
## Kanalcodierung
|
||||
Das Ziel der Kanalcodierung ist das Erkennen und/oder Beheben von Fehlern.
|
||||
|
||||
### Fehlerkorrekturverfahren
|
||||
#### Backward Error Correction
|
||||
Unter dem Prinzip der Backward Error Correction (Rückwärtsfehlerkorrektur) versteht man, dass Fehler in Daten **lediglich erkannt** werden, um diese dann erneut beim Sender anzufordern.
|
||||
|
||||
Mögliche Hilfsmittel hierfür sind bspw.:
|
||||
- Blockcodes
|
||||
- CRC (Cyclic redundancy check (siehe [CRC](#crc)))
|
||||
|
||||
#### Forward Error Correction
|
||||
Das Prinzip der Forward Error Correction (Vorwärtsfehlerkorrektur) ist es, Fehler nicht nur zu erkennen sondern direkt beim Empfang zu korrigieren.
|
||||
|
||||
Mögliche Hilfsmittel sind:
|
||||
- Blockcodes
|
||||
- Minimum-Distance-Decoding
|
||||
- Faltungscodes
|
||||
|
||||
Verfahren, die bei jedem Versand eines Pakets auf eine Antwort, dass der Versand erfolgreich war, warten, kosten viel Performance:
|
||||
|
||||

|
||||
|
||||
Aus diesem Grund ist bspw. das Protokoll TCP, welches eine Flusskontrolle hat, um einiges langsamer als UDP, welches **keine** Flusskontrolle hat.
|
||||
|
||||
### Binäre Kanäle
|
||||
Binäre Kanäle können nur die Werte $0$ und $1$ übertragen.
|
||||
|
||||
Alle Beispiele unterliegen der Annahme, dass ein symmetrischer, binärer Kanal vorliegt (siehe [Binary Symmetric Channel](#binary-symmetric-channel)).
|
||||
|
||||

|
||||
|
||||
#### Bitfehlerwahrscheinlichkeit
|
||||
Die eingezeichnete Störquelle sorgt dafür, dass zu einer Wahrscheinlichkeit $\varepsilon$ eine $0$ statt einer $1$ oder eine $1$ statt einer $0$ gesendet wird.
|
||||
|
||||
Die Bit Error ***Ratio*** `BER` (Formelbuchstabe $\varepsilon$) beschreibt, wie hoch die Wahrscheinlichkeit ist, dass ein Fehler auftritt.
|
||||
|
||||
Einige Beispiele von Fehlerwahrscheinlichkeiten:
|
||||
- Alle Bits falsch:
|
||||
$\text{BER} = 1$
|
||||
- Alle Bits richtig:
|
||||
$\text{BER} = 0$
|
||||
- 1 von 2 Bits falsch:
|
||||
$\text{BER} = 0.5$
|
||||
- 1 von 1000 Bits falsch:
|
||||
$\text{BER} = 0.001$
|
||||
|
||||
Ein asymmetrischer Kanal hat unterschiedliche Wahrscheinlichkeiten:
|
||||
- $\varepsilon_{0 \rightarrow 1}$: Die Wahrscheinlichkeit, dass eine $0$ durch einen Fehler zu einer $1$ wird
|
||||
- $\varepsilon_{1 \rightarrow 0}$: Die Wahrscheinlichkeit, dass eine $1$ durch einen Fehler zu einer $0$ wird
|
||||
|
||||
|
||||
#### Binary Symmetric Channel
|
||||
In einem symmetrischen Kanal sind diese beiden Wahrscheinlichkeiten identisch:
|
||||
$$\varepsilon_{0 \rightarrow 1} = \varepsilon_{1 \rightarrow 0} = \varepsilon$$
|
||||
|
||||
Bildlich sieht das folgendermassen aus:
|
||||

|
||||
|
||||
Wahrscheinlichkeit, dass 1 Bit korrekt übertragen wird:
|
||||
$$1-\varepsilon$$
|
||||
|
||||
Wahrscheinlichkeit, dass $N$ Bits korrekt übertragen werden:
|
||||
$$(1-\varepsilon)^N$$
|
||||
|
||||
#### Mehrbitfehlerwahrscheinlichkeit Berechnen
|
||||
In einem BSC lässt sich mit Hilfe folgender Formel berechnen, ob in einer Sequenz von $N$ Bits **genau $F$ Bitfehler** auftreten:
|
||||
|
||||
$$P_{F,N} = \underbrace{\begin{pmatrix}
|
||||
N \\
|
||||
F
|
||||
\end{pmatrix}}_{\text{Anzahl möglicher Anordnungen der Fehler}} \cdot \overbrace{\varepsilon^F}^{\text{Wahrscheinlichkeit für F Fehler}} \cdot \underbrace{(1-\varepsilon)^{N - F}}_{\text{Wahrscheinlichkeit, dass alle weiteren Bits korrekt sind}}$$
|
||||
|
||||
$\begin{pmatrix}
|
||||
N \\
|
||||
F
|
||||
\end{pmatrix}$ berechnet sich hierbei folgendermassen:
|
||||
|
||||
$$\begin{pmatrix}
|
||||
N \\
|
||||
F
|
||||
\end{pmatrix} = \frac{N!}{F! \cdot (N - F)!}$$
|
||||
|
||||
Alternativ kann das Ergebnis von $\begin{pmatrix}
|
||||
N \\
|
||||
F
|
||||
\end{pmatrix}$ auch aus dem Pascalschen Dreieck abgelesen werden:
|
||||
|
||||

|
||||
|
||||
#### Wahrscheinlichkeiten in einem BSC
|
||||
Folgende Grafik zeigt zudem auf, wie die Wahrscheinlichkeiten in einem BSC aussehen:
|
||||
|
||||

|
||||
|
||||
Mit Hilfe der im Kapitel [Entropie](#entropie-hx) erwähnten Formel lassen sich zudem auch die Entropien der einzelnen Fälle berechnen:
|
||||
|
||||

|
||||
|
||||
Zwar erhöht der Bitfehler, wie zu sehen, die Entropie, zerstört aber gleichzeitig auch Informationen vom Eingang.
|
||||
|
||||
Um also den resultierenden, tatsächlichen unversehrten Informationsgehalt zu errechnen, muss von der resultierenden Entropie $H(Y)$ die Entropie des Bitfehlers $H(\varepsilon)$ abgezogen werden.
|
||||
|
||||
$$I_{BSC} = H(Y) - H(\varepsilon)$$
|
||||
|
||||
Die gesamthafte Entropie der Störquelle $H(\varepsilon)$ berechnet sich mit dieser Formel:
|
||||
|
||||
$$H(\varepsilon) = \varepsilon \cdot \log_2\left(\frac{1}{\varepsilon}\right) + (1 - \varepsilon) \cdot \log_2\left(\frac{1}{1 - \varepsilon}\right)$$
|
||||
|
||||
Daraus ergibt sich diese Rechnung zum Bestimmen der Kapazität des BSCs aus der Abbildung:
|
||||
|
||||
$$I_{BSC} = H(Y) - H(\varepsilon) = 0.323 - \left(0.01 \cdot \log_2\left(\frac{1}{0.01}\right) + (1 - 0.01) \cdot \left(\frac{1}{1 - 0.01}\right)\right) = 0.323 - 0.081 = 0.242 Bit/Bit$$
|
||||
|
||||
Folgender Graph zeigt das Verhältnis zwischen der Bitfehler-Rate und der Kanalkapazität auf:
|
||||
|
||||

|
||||
|
||||
### Binäre Kanalcodes
|
||||
Binäre Kanalcodes sind eine Sammlung Codewörter, welche zusätzlich zu den Daten auch Informationen zwecks Fehlerschutz beinhalten können:
|
||||
|
||||

|
||||
|
||||
#### Code-Rate
|
||||
Die Code-Rate $R$ gibt an, zu wieviel Prozent Code-Wörter aus verwertbaren Informationen bestehen.
|
||||
|
||||
Sie errechnet sich aus der gesamtlänge der Code-Wörter $N$ und der Anzahl Informations-Bits $K$:
|
||||
|
||||
$$R = \frac{K}{N}$$
|
||||
|
||||
#### Hamming-Distanz
|
||||
Die minimale Hamming-Distanz $d_\text{min}$ gibt wider, wieviele Bits mindestens wechseln müssen, um aus einem Codewort ein anderes zu bilden.
|
||||
|
||||
Die Anzahl erkennbarer Fehler ist $d_\text{min}-1$
|
||||
|
||||
Die Anzahl _korrigierbarer_ Fehler $\frac{d_\text{min}-1}{2}$
|
||||
|
||||
##### Beispiele
|
||||
Folgend einige Beispiele anhand einer 3-Bit Codes.
|
||||
|
||||
###### Hamming Distanz 1
|
||||
Ein Fehler führt zu einer Verwechslung mit einem anderen Codewort:
|
||||
|
||||

|
||||
|
||||
###### Hamming Distanz 2
|
||||
Maximal 1 Bitfehler (orange hinterlegt) kann erkannt werden:
|
||||
|
||||

|
||||
|
||||
###### Hamming Distanz 3
|
||||
Maximal 2 Bitfehler erkennbar, maximal 1 Bitfehler korrigierbar:
|
||||
|
||||

|
||||
|
||||
#### Hamming-Gewicht
|
||||
Das Hamming-Gewicht $w_H(x)$ bezeichnet die Anzahl in einem Code-Wort.
|
||||
|
||||
> ***Beispiele:***
|
||||
> - $w_H(000) = 0$
|
||||
> - $w_H(001) = w_H(010) = w_H(100) = 1$
|
||||
> - $w_H(110) = w_H(101) = w_H(011) = 2$
|
||||
> - $w_H(111) = 3$
|
||||
|
||||
Mit Hilfe des Hamming-Gewitchs lässt sich die Hamming-Distanz mathemtaisch berechnen:
|
||||
|
||||
$$d(x, y) = w_H(x \oplus y)$$
|
||||
|
||||
#### Eigenschaften von Binären Kanalcodes
|
||||
##### Perfekt
|
||||
Alle möglichen Sequenzen haben eine minimale Hamming-Distanz zu einem korrekten Code-Wort zu dem es somit zugewiesen werden kann.
|
||||
|
||||
##### Systematisch
|
||||
Die Informations-Bits (die zu versendenden Daten) sind an einem Stück
|
||||
|
||||
Beispiele:
|
||||
|
||||

|
||||
|
||||
oder
|
||||
|
||||

|
||||
|
||||
##### Linear
|
||||
Zwei beliebige gültige Code-Wörter geben, rechnet man sie mit `XOR` $\oplus$ zusammen, wiederum ein gültiges Code-Wort.
|
||||
|
||||
> ***Hinweis:***
|
||||
> Durch Generator-Matrizen erstellte Codes sind **immer** linear (siehe [Lineare Block-Codes](#lineare-block-codes)).
|
||||
>
|
||||
> Ob ein Block-Code linear ist kann nur mit Sicherheit überprüft werden, indem man alle Code-Wörter untereinander mit `XOR` $\oplus$ zusammenrechnet und prüft, ob das Ergebnis ein gültiges Code-Wort ist.
|
||||
|
||||
##### Zyklisch
|
||||
Die zyklische Verschiebung eines gültigen Code-Wortes ergibt ein gültiges Codewort:
|
||||
|
||||

|
||||
|
||||
Beispiele dazu:
|
||||
|
||||

|
||||
|
||||
## Fehlererkennung
|
||||
### Paritäts-Check
|
||||
Der einfachste Weg, Daten auf deren Gültigkeit zu prüfen. Für den Paritäts-Check werden alle Bits eines Datenstroms mit `XOR` $\oplus$ zusammengerechnet. Das Ergebnis ist die sogenannte Parität. Ist diese beim Empfang der Daten ungültig, so ist beim Versand ein Fehler aufgetreten.
|
||||
|
||||
Beispiel eines Paritäts-Checks:
|
||||
|
||||

|
||||
|
||||
### Cyclic Redundancy Check CRC
|
||||
Der Cyclic Redundancy Check (oder CRC) ist ein Algorithmus zum einfachen Prüfen eines Datenstroms auf Fehler.
|
||||
|
||||
Um eine CRC Prüfsumme zu erstellen und zu prüfen, muss man sich vorgängig auf ein Generator Polynom einigen (das heutzutage gängigste ist bspw. `crc32`).
|
||||
|
||||
Um den CRC zu berechnen, muss dem Datenstrom die Anzahl Stellen des Generator-Polynoms minus 1 angefügt werden (grau hinterlegt). Die daraus errechnete Zahl muss anschliessend durch das Generator-Polynom (blau hinterlegt) dividiert werden.
|
||||
|
||||
Der daraus entstehende Rest (rot hinterlegt) ist die CRC Prüfsumme.
|
||||
|
||||

|
||||
|
||||
Anschliessend wird der Datenstrom zusammen mit dem CRC (an Stelle des grau hinterlegten Platzhalters) versendet.
|
||||
|
||||
Geprüft wird die Gültigkeit indem der ankommende Datenstrom durch das Generator-Polynom geteilt wird. Ist der Rest $0$, so sind die Daten korrekt:
|
||||
|
||||

|
||||
|
||||
## Fehlerkorrektur
|
||||
Ander als in der Fehlererkennung sollen in der Fehlererkennung einige Fehler auch ohne weiteres beim Empfänger korrigiert werden können.
|
||||
|
||||
Das Konzept sieht hierbei folgend aus:
|
||||
|
||||

|
||||
|
||||
Die Formel zum Errechnen von der Anzahl Prüfbits $P$ für die Übertragung von $K$ Informations-Bits:
|
||||
|
||||
$p \approx I(K + 1)$
|
||||
|
||||
Für 200 Informations-Bits:
|
||||
|
||||
$p \approx \log_2(200 + 1) = 7.6\text{ bit} \approx 8\text{ bit}$
|
||||
|
||||
### Lineare Block-Codes
|
||||
Hamming Codes gehören zu den linearen Block-Codes.
|
||||
|
||||
Lineare Block-Codes werden mit Hilfe einer Generatormatrix gebildet, welche aus einer Paritäts-Matrix und einer Einheits-Matfix besteht:
|
||||
|
||||

|
||||
|
||||
Die Paritätsmatrix wird verwendet, um die Prüfsumme zu erstellen, die Einheitsmatrix, um die eigentliche Information einzufügen.
|
||||
|
||||
Berechnet werden die generierten Bits ähnlich wie in einer Matrix Rechnung.
|
||||
|
||||
Will man bspw. die Daten `0101` versenden, ist die Rechnung für das 1. Bit folgendermassen:
|
||||
|
||||
Die erste Spalte für das 1. Bit befindet sich in der Paritätsmatrix und lautet `1011`.
|
||||
|
||||
Die Rechnung ist $(0 \wedge 1) \oplus (1 \wedge 0) \oplus (0 \wedge 1) \oplus (1 \wedge 1) = 1$
|
||||
|
||||
Folgend sieht die Lösung für das Berechnen aller Bits aus:
|
||||
|
||||

|
||||
|
||||
Die Prüfmatrix kann gebildet werden, indem die horizontale Einheitsmatrix entfernt und durch eine vertikale Einheitsmatrix ersetzt wird:
|
||||
|
||||

|
||||
|
||||
Berechnet man auf dieselbe Weise wie zuvor das Produkt eines Code-Wortes mit der Prüf-Matrix erhält man als Ergebnis $0$, falls die Übertragung korrekt war.
|
||||
|
||||
Ansonsten erhält man das sogenannte "Syndrom" des Indexes des Bits, welches falsch übertragen wurde:
|
||||
|
||||

|
||||
|
||||
## Faltungscode
|
||||
Folgendes Bild zeigt auf, wie mit Hilfe eines Trellis-Diagramms ein Faltungscode errechnet und auch wieder decodiert wird:
|
||||
|
||||

|
||||
|
||||
Die freie Hamming-Distanz kann am einfachsten vom Zustandsdiagramm abgelesen werden.
|
||||
|
||||
### Schaltungs-Umsetzung eines Faltungscodes
|
||||

|
||||
|
||||
## Glossar
|
||||
| Wort | Definition |
|
||||
| ----------------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------ |
|
||||
| Zahlensystem | System zum Darstellen von Zahlen (bspw. Dezimalsystem, Hexadezimal-System siehe [Zahlensysteme](#zahlensysteme)) |
|
||||
| Bit (Binary Digit) | Speicher für 1 Bit (`true`/`false`) |
|
||||
| Byte (Octet) | 8 Bit oder 2 Nibble à 4 Bit  |
|
||||
| Word | Wert mit (meist) 16 Bit:  |
|
||||
| Doubleword (`DWord`) | Aneinanderreihung von 2 Worten:  |
|
||||
| Quadword (`QWord`) | Aneinanderreihung von 4 Worten |
|
||||
| Octaword | Aneinanderreihung von 8 Worten |
|
||||
| DMS | Eine DMS - Discrete Memoryless Source - liefert voneinander unabhängige, zufällige Werte |
|
||||
| BMS | Eine BMS - Binary Memoryless Source - liefert voneinander unabhängige, zufällige binäre Werte ($0$en und $1$en) |
|
||||
| Probability $P(x)$ | Die Wahrscheinlichkeit, dass das Symbol $x$ in einer Nachricht auftritt (siehe [Probability](#probability-px)) |
|
||||
| Informationsgehalt $I(x)$ | Der Informationsgehalt, der ein übermitteltes Symbol hat (siehe [Informationsgehalt](#informationsgehalt-ix)) |
|
||||
| Entropie $H(x)$ | Der durchschnittliche Informationsgehalt einer Quelle (siehe [Entropie](#entropie-hx)) |
|
||||
| Mittlere Codewortlänge $L(x)$ | Die durchschnittliche Länge, welche die Codeworte einer Codierung haben (siehe [Codewortlänge](#mittlere-symbollänge-lx)) |
|
||||
| Redundanz $R(x)$ | Die Redundanz beschreibt, wieviele unnötige Daten Codeworte einer Codierung enthalten. Eine niedrige Redundanz ist besser. (siehe [Redundanz](#redundanz-einer-codierung-rx)) |
|
||||
| `RLE` (Run Length Encoding) | Codierung in der ein sich oft wiederholendes Symbol komprimiert darstellen lässt (siehe [RLE](#run-length-encoding-rle)) |
|
||||
| Luminanz $Y$ | Graustufen-Intensität (siehe [JPEG](#jpeg-kompressionsverfahren)) |
|
||||
| Spiegelung | Eine der möglichen Fehlern, die beim Digitalisieren eines Audiosignals auftreten kann (siehe [Abtasttheorem](#abtasttheorem)) |
|
||||
| Backward Error Correction | Das Erkennen von Fehlern in empfangenen Daten |
|
||||
| Bit Error Ratio `BER` | Die Bit Error Ratio beschreibt, wie hoch die Wahrscheinlichkeit ist, dass Bit-Fehler in einem Binären Kanal auftreten. (siehe [Bitfehlerwahrscheinlichkeit](#bitfehlerwahrscheinlichkeit)) |
|
||||
| Hamming-Distanz | Die minimale Anzahl unterschiedlicher Bits zwischen 2 Code-Worten in einem Blockcode (siehe [Hamming-Distanz](#hamming-distanz)) |
|
||||
| Hamming-Gewicht | Die Anzahl $1$en in einem Code-Wort (siehe [Hamming-Gewicht](#hamming-distanz)) |
|
||||
| Code-Rate $R$ | Die Code-Rate beschreibt, das Verhältnis der Anzahl Informationsbits gegenüber der gesamtlänge der Codewörter (siehe [Code-Rate](#coderate)) |
|
||||
| Syndrom | Ein Wert, der darauf hinweist, dass an einer gewissen Bit-Stelle ein Fehler geschehen ist. |
|
||||
|
After 
(image error) Size: 7.7 KiB |
|
After 
(image error) Size: 54 KiB |
|
After 
(image error) Size: 14 KiB |
BIN
Notes/Semester 1/INCO - Informatik und Codierung/assets/BSC.png
Normal file
|
After 
(image error) Size: 64 KiB |
|
After 
(image error) Size: 50 KiB |
|
After 
(image error) Size: 59 KiB |
|
After 
(image error) Size: 76 KiB |
|
After 
(image error) Size: 28 KiB |
|
After 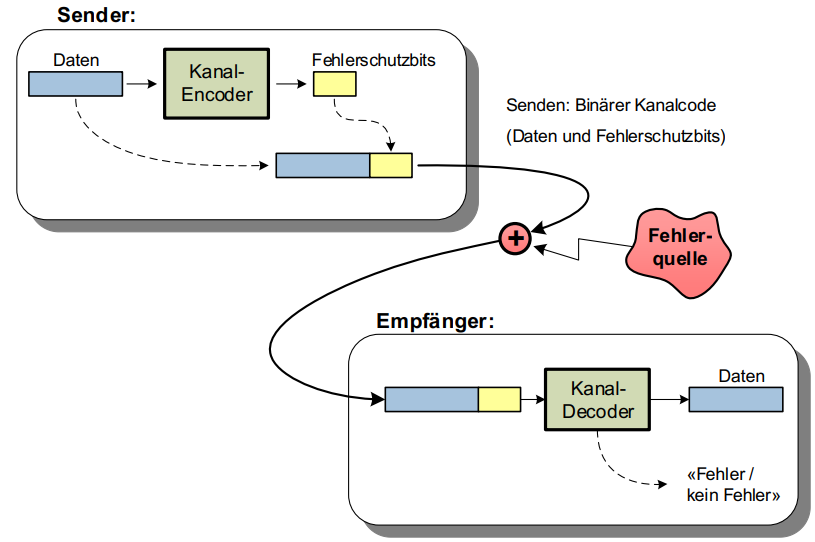
(image error) Size: 53 KiB |
|
After 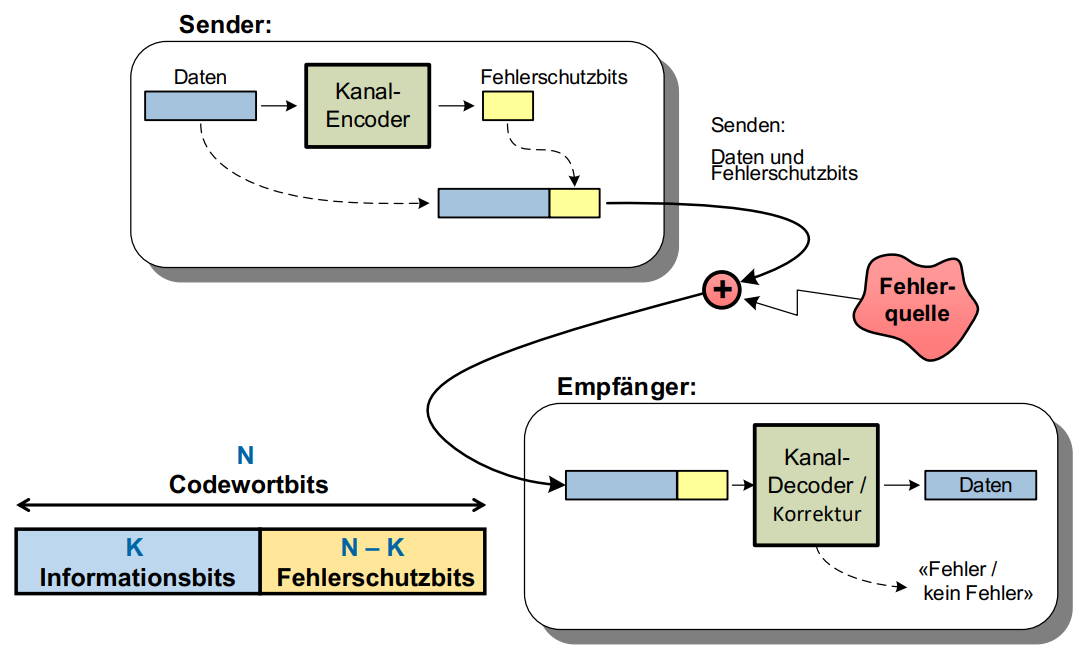
(image error) Size: 79 KiB |
|
After 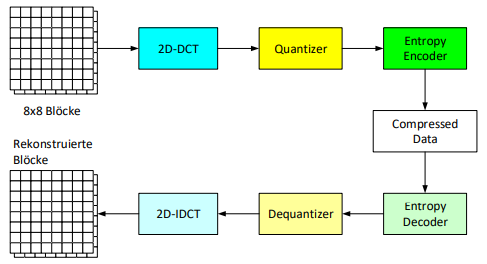
(image error) Size: 20 KiB |
|
After 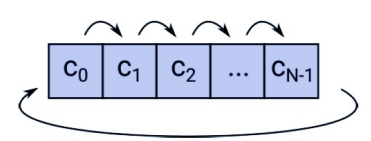
(image error) Size: 28 KiB |
|
After 
(image error) Size: 31 KiB |
|
After 
(image error) Size: 175 KiB |
|
After 
(image error) Size: 9.4 KiB |
|
After 
(image error) Size: 66 KiB |
|
After 
(image error) Size: 24 KiB |
|
After 
(image error) Size: 12 KiB |
|
After 
(image error) Size: 15 KiB |
|
After 
(image error) Size: 131 KiB |
|
After 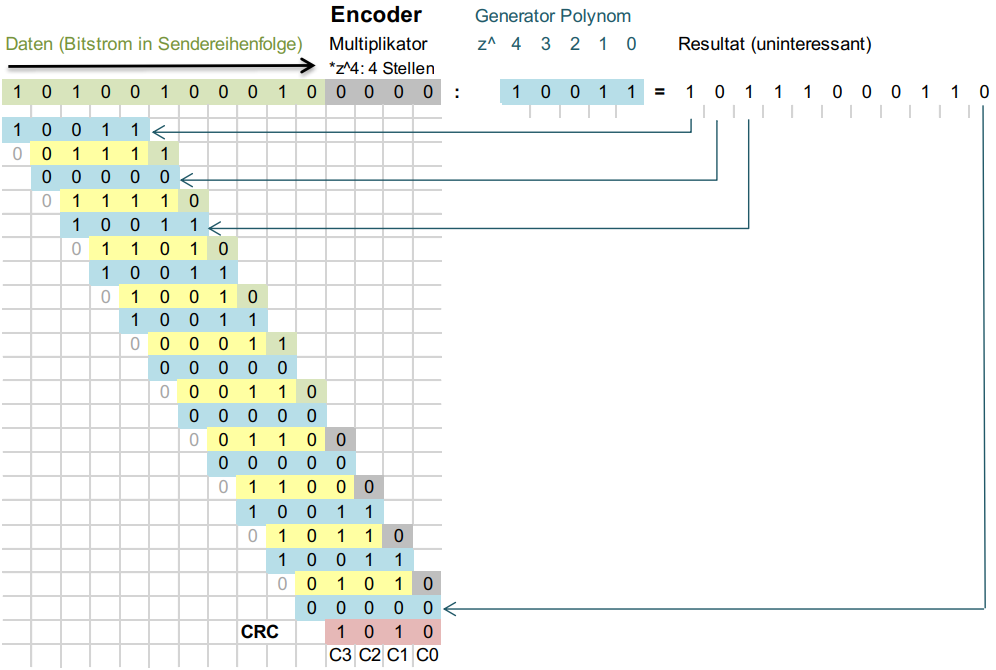
(image error) Size: 67 KiB |
|
After 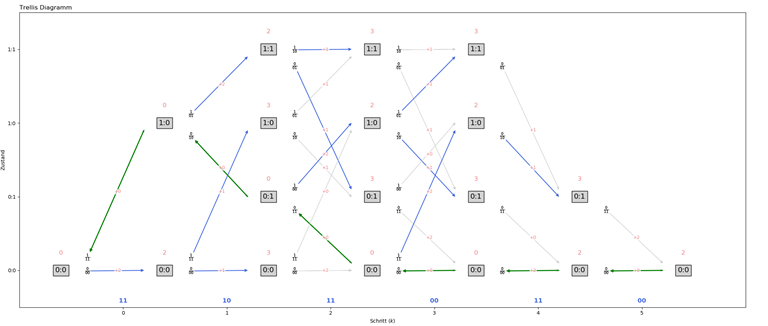
(image error) Size: 39 KiB |
|
After 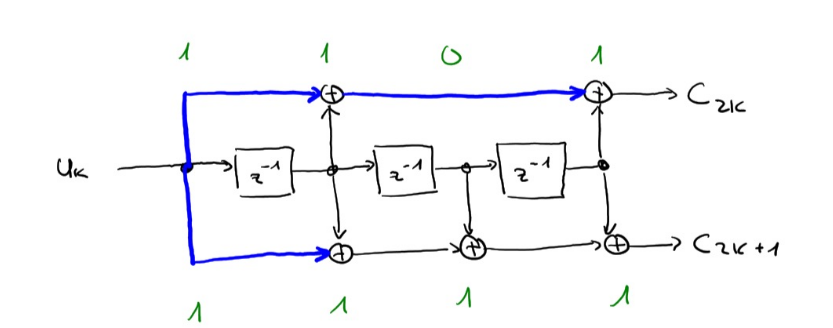
(image error) Size: 78 KiB |
|
After 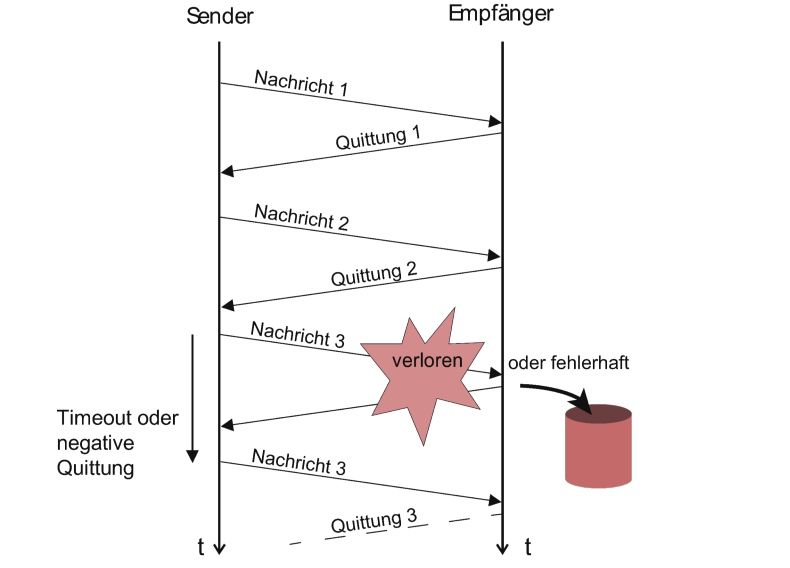
(image error) Size: 62 KiB |
|
After 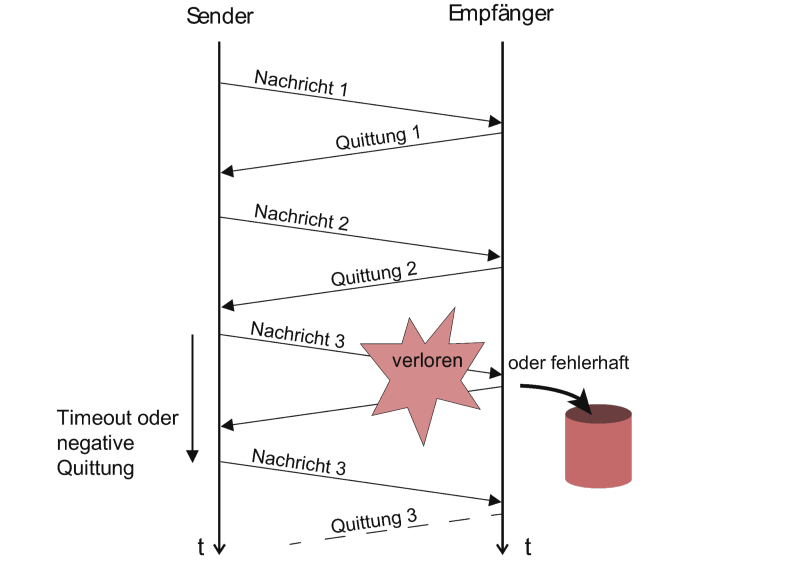
(image error) Size: 62 KiB |
|
After 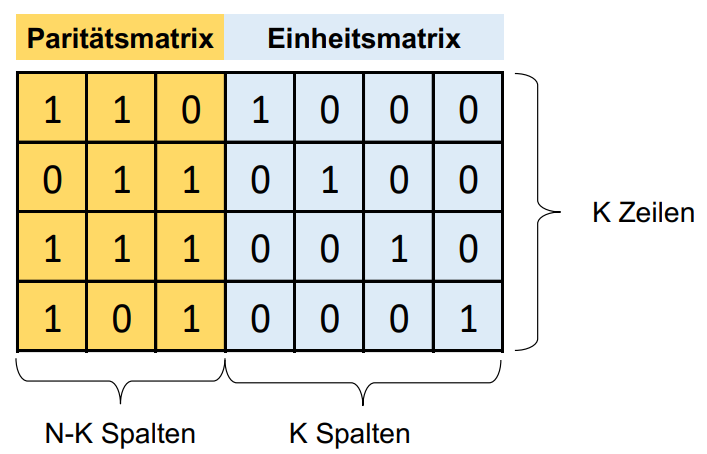
(image error) Size: 35 KiB |
|
After 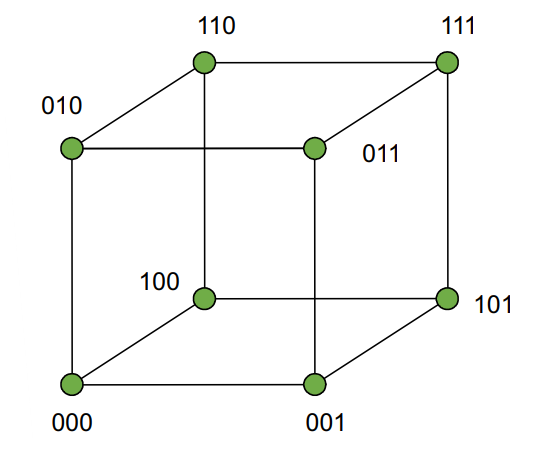
(image error) Size: 21 KiB |
|
After 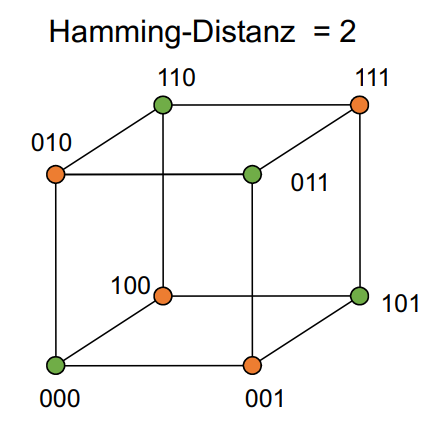
(image error) Size: 22 KiB |
|
After 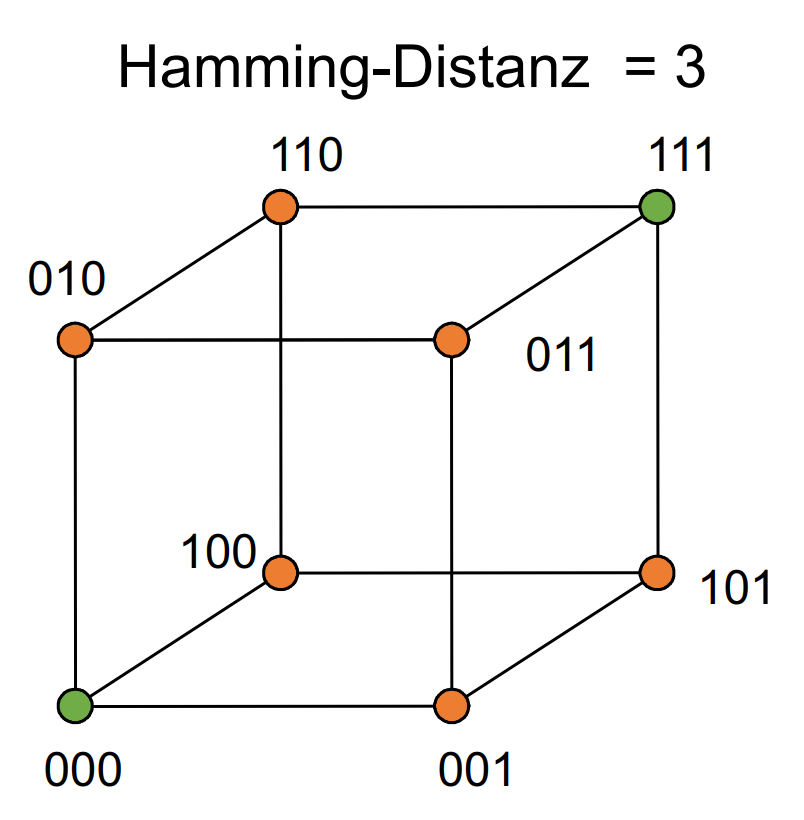
(image error) Size: 48 KiB |
|
After 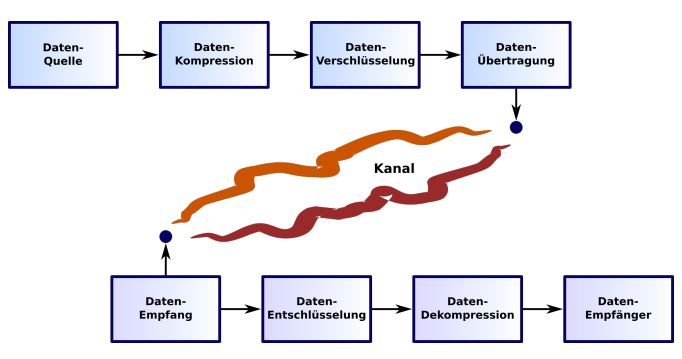
(image error) Size: 40 KiB |
|
After 
(image error) Size: 133 KiB |
|
After 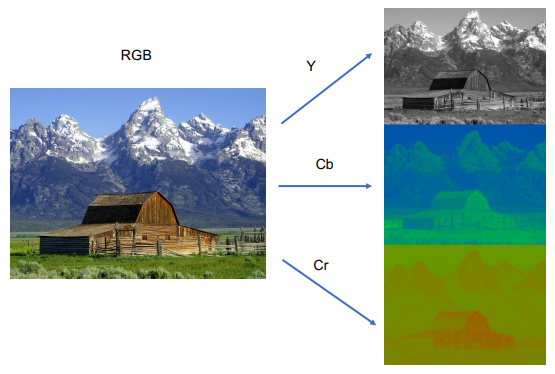
(image error) Size: 184 KiB |
BIN
Notes/Semester 1/INCO - Informatik und Codierung/assets/LZ77.png
Normal file
|
After 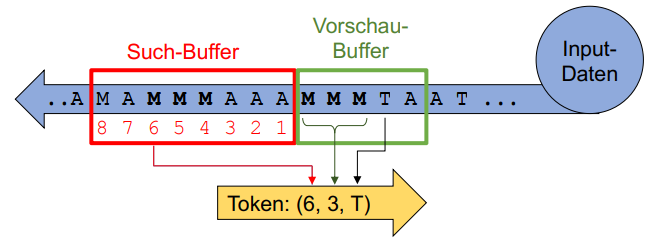
(image error) Size: 24 KiB |
BIN
Notes/Semester 1/INCO - Informatik und Codierung/assets/LZW.png
Normal file
|
After 
(image error) Size: 11 KiB |
|
After 
(image error) Size: 150 KiB |
|
After 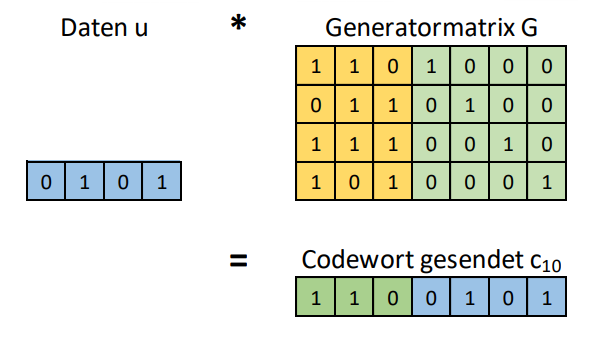
(image error) Size: 21 KiB |
|
After 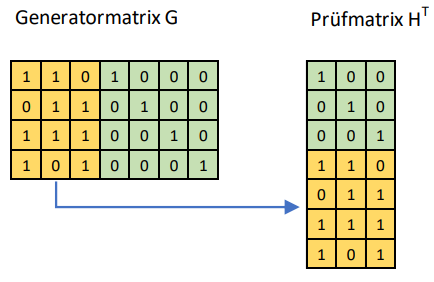
(image error) Size: 14 KiB |
|
After 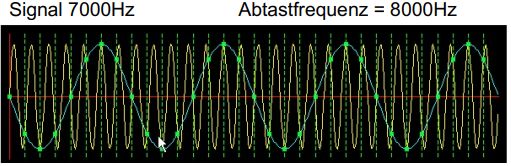
(image error) Size: 113 KiB |
|
After 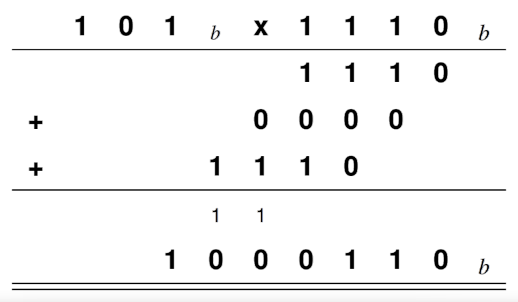
(image error) Size: 15 KiB |
|
After 
(image error) Size: 6.4 KiB |
|
After 
(image error) Size: 45 KiB |
|
After 
(image error) Size: 24 KiB |
|
After 
(image error) Size: 290 KiB |
|
After 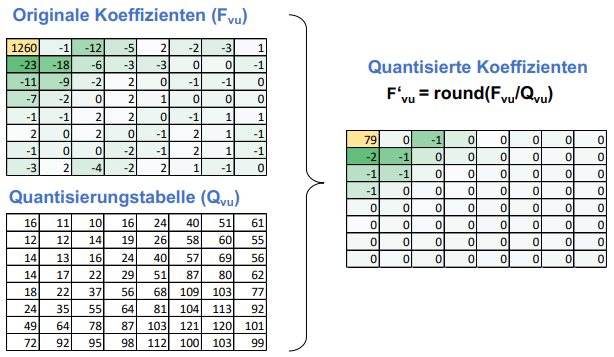
(image error) Size: 52 KiB |
|
After 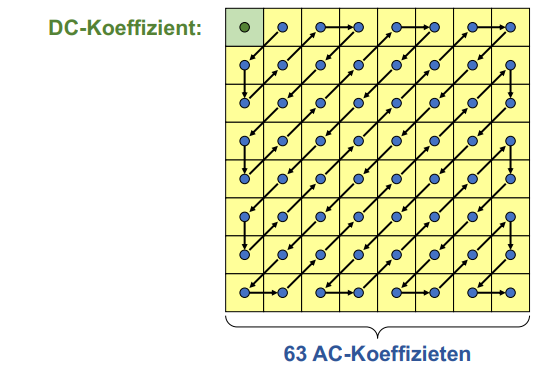
(image error) Size: 45 KiB |
|
After 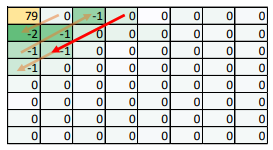
(image error) Size: 12 KiB |
|
After 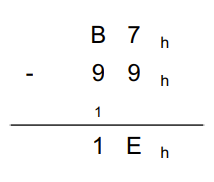
(image error) Size: 4.2 KiB |
|
After 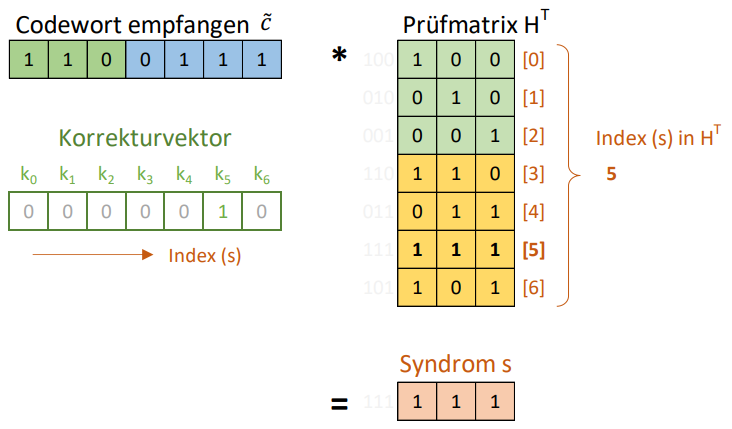
(image error) Size: 39 KiB |
|
After 
(image error) Size: 12 KiB |
|
After 
(image error) Size: 12 KiB |
BIN
Notes/Semester 1/INCO - Informatik und Codierung/assets/Word.png
Normal file
|
After 
(image error) Size: 7.8 KiB |
5
Notes/Semester 1/PROG1 - Programmieren/Bücher.md
Normal file
|
|
@ -0,0 +1,5 @@
|
|||
# Bücher
|
||||
Folgende Bücher müssen gekauft werden:
|
||||
|
||||
* ISBN 978-3-86894-911-7
|
||||
* ISBN 978-0-13-235088-4
|
||||
15
Notes/Semester 1/PROG1 - Programmieren/OOP.md
Normal file
|
|
@ -0,0 +1,15 @@
|
|||
# Objekt-Orientierte Programmierung
|
||||
## Klassen
|
||||
Definitionen von Instanzen einer Objekt-Art - der "Bauplan" - nennt sich `Klasse`.
|
||||
|
||||
Die Klasse gibt vor, wie dessen Instanzen aufgebaut sind. So könnte bspw. eine Klasse für ein `Auto` in einem GTA-Spiel Eigenschaften wie `Velocity` (Beschläunigung), `Color` (Farbe) oder `Model` (Modell) haben.
|
||||
|
||||
Will man jedoch kein GTA-Spiel sondern - möglicherweise - ein Programm für einen Auto-Makler erstellen, sind wiederum andere Eigenschaften von Wichtigkeit wie bspw. der `Price` (Preis) oder das `Brand` (die Marke).
|
||||
|
||||
## Instanzen
|
||||
Instanzen sind Objekte, die anhand einer [Klasse](#klassen) erstellt wurde. Diese haben alle in der Klasse vorgeschriebene Eigenschaften, Felder und Methoden. Einer Instanz kann man konkrete Werte für die Eigenschaften zuweisen.
|
||||
|
||||
So könnte man eine Objekt-Instanz `expensiveCar` der `Auto`-Klasse erstellen, welche das `Brand` `BMW` hat und eine Objekt-Instanz `CheapCar`, welche das `Brand` `Škoda` hat.
|
||||
|
||||
## Bezeichnungen
|
||||
Sämtliche Komponenten eines Projekts (Variablen (`variable`s), Parameter (`parameter`s), Klassen (`class`es), Felder (`field`s), Eigenschaften (`Property`/Properties) und Methoden (`Method`s)) müssen benannt werden. Hierbei ist wichtig, auf möglichst prägnante Bezeichnungen zurückzugreifen.
|
||||
|
|
@ -0,0 +1 @@
|
|||
# Inhaltsverzeichnis
|
||||
4
Notes/Semester 1/Table of Contents.md
Normal file
|
|
@ -0,0 +1,4 @@
|
|||
# Inhaltsverzeichnis
|
||||
- [DB - Datenbanken](./DB%20-%20Datenbanken/Table%20of%20Contents.md)
|
||||
- [INCO - Informationen und Codierung](./INCO%20-%20Informationen%20und%20Codierung/Table%20of%20Contents.md)
|
||||
- [DM - Diskrete Mathematik](./DM%20-%20Diskrete%20Mathematik/Table%20of%20Contents.md)
|
||||
239
Notes/Semester 2/AN2 - Analysis 2/Analysis 2.ipynb
Normal file
145
Notes/Semester 2/AN2 - Analysis 2/Zusammenfassung.md
Normal file
|
|
@ -0,0 +1,145 @@
|
|||
<script src="../../../assets/deployggb.js"></script>
|
||||
<script src="../../../assets/graphs.js"></script>
|
||||
<script>
|
||||
window.graphs(
|
||||
[
|
||||
[
|
||||
"example",
|
||||
[
|
||||
"f(x) = x^3 + 5",
|
||||
"a = IntegralBetween(f(x), 2, 4)",
|
||||
"SetCaption(a, \"Integral\")",
|
||||
"SetCaption(f, \"f(x)\")"
|
||||
],
|
||||
undefined,
|
||||
(api) =>
|
||||
{
|
||||
api.setColor("a", 255, 0, 0);
|
||||
api.evalCommand("ZoomIn(-10, -10, 10, 100)");
|
||||
api.evalCommand("ShowLabel(a, true)");
|
||||
}
|
||||
]
|
||||
])
|
||||
</script>
|
||||
|
||||
# Zusammenfassung Analysis 2
|
||||
## Inhalt
|
||||
- [Zusammenfassung Analysis 2](#zusammenfassung-analysis-2)
|
||||
- [Inhalt](#inhalt)
|
||||
- [Integrale](#integrale)
|
||||
- [Unbestimmte Integrale](#unbestimmte-integrale)
|
||||
- [Integration von Produkten](#integration-von-produkten)
|
||||
- [Integration durch Substitution](#integration-durch-substitution)
|
||||
- [Schritt 1: Verschachtelte Funktionen Bestimmen](#schritt-1-verschachtelte-funktionen-bestimmen)
|
||||
- [Schritt 2: Substitutions-Gleichung für $x$](#schritt-2-substitutions-gleichung-für-x)
|
||||
- [Schritt 3: Substitutions-Gleichung für $dx$](#schritt-3-substitutions-gleichung-für-dx)
|
||||
- [Schritt 4: Integral-Substitution](#schritt-4-integral-substitution)
|
||||
- [Taylor-Reihe](#taylor-reihe)
|
||||
|
||||
## Integrale
|
||||
Integrale dienen dazu, die Flächen unter einer Kurve zu berechnen.
|
||||
|
||||
<p id="example"></p>
|
||||
|
||||
Mit der Funktion $f(x) = x^3 + 5$ lässt sich dessen Integral folgendermassen darstellen:
|
||||
|
||||
$$\int_{2}^4{f(x)dx}$$
|
||||
|
||||
oder
|
||||
|
||||
$$\int_{2}^4{\left(x^3 + 5\right)dx}$$
|
||||
|
||||
Berechnen lässt sich das Integral mit Hilfe der Basisfunktion:
|
||||
|
||||
$$F(x) = \frac{1}{4}x^4 + 5x$$
|
||||
|
||||
Folgend lautet die Integration:
|
||||
|
||||
$$\int_{2}^4{f(x)dx} = F(4) - F(2)$$
|
||||
|
||||
oder
|
||||
|
||||
$$\int_{2}^4{f(x)dx} = \left(\frac{1}{4}4^4 + 5 \cdot 4\right) - \left(\frac{1}{4} \cdot 2^4 + 5 \cdot 2\right) \\
|
||||
\int_{2}^4{f(x)dx} = \frac{1}{4} \cdot 256 + 20 - \frac{1}{4} \cdot 16 - 10 \\
|
||||
\int_{2}^4{f(x)dx} = 64 + 20 - 4 - 10 = 70$$
|
||||
|
||||
### Unbestimmte Integrale
|
||||
Integrale können in unbestimmter oder in bestimmter Form geschrieben werden. Unbestimmte Integrale haben - anders als bestimmte Integrale - keinen festgelegte Grenzwerte.
|
||||
|
||||
Aus diesem Grund können diese nicht eindeutig berechnet werden:
|
||||
|
||||
$$\int{x^3 + 5dx} = F(x) = \frac{1}{4}x^4 + 5x + C$$
|
||||
|
||||
> ***Informationen zur Konstanten $C$:***
|
||||
> Da in der Ableitung von $f(x) = x^3 + 5$ eine beliebige Konstante $C$ zulässt, kann die Ableitung nicht eindeutig bestimmt werden. Nur durch Setzen von Grenzen lässt sich die Konstante **eliminieren**:
|
||||
> $$\int_{-1}^1{x^3 + 5dx} = F(1) - F(-1) \\
|
||||
> \int_{-1}^1{x^3 + 5dx} = \left(\frac{1}{4} \cdot 1^4 + 5 \cdot 1 + C\right) - \left(\frac{1}{4} + 5 \cdot -1 + C\right) \\
|
||||
> \int_{-1}^1{x^3 + 5dx} = \frac{1}{4} + 5 + C - \frac{1}{4} + 5 - C \\
|
||||
> \int_{-1}^1{x^3 + 5dx} = 5 + 5 + \frac{1}{4} - \frac{1}{4} + C - C = 10$$
|
||||
|
||||
### Integration von Produkten
|
||||
Da Produkte sowohl durch Produktregel oder durch Kettenregel entstandene Ableitungen sein können, ist das Bestimmen der Basisfunktion von Produkten etwas komplizierter.
|
||||
|
||||
So kann ein Produkt von folgenden 2 Ableitungen[^Derivation] stammen:
|
||||
|
||||
$$\left(u(x) \cdot v(x) \right)' = u'(x) \cdot v(x) + u(x) \cdot v'(x)$$
|
||||
|
||||
oder
|
||||
|
||||
$$(u(v(x)))' = u'(v(x)) \cdot v'(x)$$
|
||||
|
||||
Die zwei gängigsten Methoden sind im folgenden beschrieben:
|
||||
|
||||
#### Integration durch Substitution
|
||||
Diese Methode basiert auf folgende Ableitungs-Regel[^Derivation].
|
||||
|
||||
$$F(u(x)) = \int{F(u(x))' dx} = \int{F'(u) \cdot u'(x) dx}$$
|
||||
|
||||
Gelöst wird das Ganze mit der Regel $\frac{du}{dx} = g'(x)$ für $u = g(x)$.
|
||||
|
||||
Aufgezeigt wird das anhand eines bestimmten und eines unbestimmten Integrals:
|
||||
|
||||
- Beispiel a)
|
||||
$$\int{\left(\cos(x^2) \cdot x\right) dx}$$
|
||||
- Beispiel b)
|
||||
$$\int^{\sqrt{\frac{\pi}{2}}}_0\left(\cos(x^2) \cdot x\right) dx$$
|
||||
|
||||
##### Schritt 1: Verschachtelte Funktionen Bestimmen
|
||||
In diesem Schritt sollen die verschachtelten Funktionen für spätere Funktionen bestimmt werden:
|
||||
|
||||
Für Beispiel a) und b) mit $f(g(x)) = \cos(x^2) \cdot x$:
|
||||
- $f(x) = \cos(g(x)) \cdot x$
|
||||
- $g(x) = x^2$
|
||||
|
||||
##### Schritt 2: Substitutions-Gleichung für $x$
|
||||
$$u = g(x)$$
|
||||
|
||||
Für Beispiel a) und b) bedeutet das:
|
||||
$$u = x^2$$
|
||||
|
||||
> ***Note:***
|
||||
> Eine verschachtelte Funktion wird üblicherweise mit $g(x)$ bezeichnet.
|
||||
|
||||
##### Schritt 3: Substitutions-Gleichung für $dx$
|
||||
$$\frac{du}{dx} = g'(x) \Rightarrow dx = \frac{du}{g'(x)}$$
|
||||
|
||||
Im Fall von Beispiel a) und b) entspricht die Ableitung $g'(x)$ $2x$.
|
||||
|
||||
Für Beispiel a) und b) bedeutet das folgendes:
|
||||
|
||||
$$\frac{du}{dx} = 2x \Rightarrow dx = \frac{du}{2x}$$
|
||||
|
||||
##### Schritt 4: Integral-Substitution
|
||||
$$\int{f(x) dx} = \int{\varphi(u) du}$$
|
||||
|
||||
Die genannte Formel muss nun auf das Integral und das substituierte Integral angewendet werden.
|
||||
|
||||
Hierbei soll die Variable $x$ weggekürzt werden. Ist dies nicht möglich, so ist dieser Ansatz "Integration durch Substitution" für dieses Integral nicht möglich.
|
||||
|
||||
***Beispiel a)***
|
||||
$$\int{\left(\cos(x^2) \cdot x\right) dx} = \int{\left(\cos(u) \cdot x\right) \frac{du}{2x}} \\
|
||||
\int{\left(\cos(x^2) \cdot x\right) dx}$$
|
||||
|
||||
## Taylor-Reihe
|
||||
|
||||
[^Derivation]: [Ableitungen](../.../../../Semester%201/AN1%20-%20Analysis%201/Ableitungen.md)
|
||||
|
|
@ -0,0 +1,24 @@
|
|||
# IP-Adressierung
|
||||
## Adressierung im L3
|
||||
- Hierarchisch
|
||||
|
||||
### Subnetting
|
||||
Mögliche Zahlen in Subnetzmasken:
|
||||
|
||||
|
||||
| Wert (dezimal) | Wert (Hexadezimal) | Wert (Binär) | Alternative Schreibweise | Anzahl adressierbarer Interfaces |
|
||||
| :------------: | :----------------: | :-------------------------------------: | ------------------------ | :------------------------------: |
|
||||
| 255.255.255.0 | 0xFFFFFF00 | 1111'1111'1111'1111'1111'1111'0000'0000 | /24 | $256 - 2$ |
|
||||
| 255.255.254.0 | 0xFFFFFE00 | 1111'1111'1111'1111'1111'1110'0000'0000 | /23 | $512 - 2$ |
|
||||
| 255.255.252.0 | 0xFFFFFC00 | 1111'1111'1111'1111'1111'1100'0000'0000 | /22 | $1024 - 2$ |
|
||||
| 255.255.248.0 | 0xFFFFF800 | 1111'1111'1111'1111'1111'1000'0000'0000 | /21 | $2048 - 2$ |
|
||||
| 255.255.240.0 | 0xFFFFF000 | 1111'1111'1111'1111'1111'0000'0000'0000 | /20 | $4096 - 2$ |
|
||||
| 255.255.224.0 | 0xFFFFE000 | 1111'1111'1111'1111'1110'0000'0000'0000 | /19 | $8192 - 2$ |
|
||||
| 255.255.192.0 | 0xFFFFC000 | 1111'1111'1111'1111'1100'0000'0000'0000 | /18 | $16384 - 2$ |
|
||||
| 255.255.128.0 | 0xFFFF8000 | 1111'1111'1111'1111'1000'0000'0000'0000 | /17 | $32768 - 2$ |
|
||||
| 255.255.0.0 | 0xFFFF0000 | 1111'1111'1111'1111'0000'0000'0000'0000 | /16 | $65536 - 2$ |
|
||||
|
||||
## Routing
|
||||
## IP-Adressen/Header
|
||||
## ARP, Kapselung
|
||||
## Fragmentierung
|
||||