manuth/ZHAWNotes
1
0
Fork 0
Code Issues Pull requests Projects Releases Wiki Activity
ZHAWNotes/Notes/Semester 3/HM1 - Höhere Mathematik/Zusammenfassung.md

31 KiB
Raw Blame History

Höhere Mathematik

Inhalt

Einführung

Einsatzgebiet

  • Annähern komplexer Formeln in endlicher Zeit
  • Berechnung von Algorithmen durch Computer
    • Algorithmen ohne expliziter Lösungsdarstellung
    • Alternative Lösungsvorgänge für höhere Performance

Arten von Lösungen

  • Direkte Verfahren - Exakte Lösung nach endlicher Zeit
  • Näherungsverfahren/Iteratives Verfahren - Approximation nach begrenzter Anzahl Rechenschritte

Verbindung zur Informatik

  • Effiziente Berechnung numerischer Algorithmen
  • Speicherung und Darstellung von Zahlen
  • Computergrafik & Bildverarbeitung
  • Neuronale Netze

Typische Fragestellungen

  • Wie wirkt sich die Beschränkung der Anzahl Bits für Zahlenformate auf Rechenergebnisse und Rechengenauigkeit aus?
  • Numerische Lösung von Nullstellenproblemen
  • Numerische Integration

Rechnerarithmetik

Maschinenzahl

Maschinenzahlen werden als Zahlen x in folgender Form dargestellt:

x = m \cdot B^e

  • x: Die zu repräsentierende Zahl
  • m: Die Mantisse (der darstellbare Zahlenwert)
  • B: Die Basis der zu repräsentierenden Zahl
  • e: Der Exponent (der Stellenwert der Mantisse m)

Beispiel: 1337 = 0.1337 * 10^4

Maschinenzahlen sind normalisiert, wenn

  • für die Mantisse m 0.1 <= |m| < 1.0 zutrifft

Maschinenzahlen werden normalisiert, damit es zu jedem Wert eine eindeutige Darstellung als Maschinenzahl gibt.

Grenzen von Maschinenzahlen

x_{max} = B^{e_{max}} - B^{e_{max}-n} = (1 - B^{-n}) \cdot B^{e_{max}}

x_min = B^{e_{min} - 1}

Datentypen gem. IEEE

float oder single: 32 Bit - 1 Bit für Vorzeichen, 23 Bit für Mantisse m, 8 Bit für Exponent e

double: 64 Bit - 1 Bit für Vorzeichen, 52 für Mantisse m, 11 Bit für Exponent e

Rundungsfehler und Maschinengenauigkeit

Absoluter Fehler:

|\tilde{x} - x|

Relativer Fehler:

\frac{|\tilde{x} - x|}{|x|}

Maximaler absoluter Rundungsfehler:

\frac{B}{2} \cdot B^{e - n - 1}

Maschinengenauigkeit oder maximaler relativer Rundungsfehler:

\frac{1}{2} \cdot B^{1 - n}

Fehlerfortpflanzung bei Funktionsauswertung:

Relativ:

\frac{f'(x) \cdot x}{f(x)} \cdot \frac{\tilde{x} - x}{x}

Absolut:

|f'(x)| \cdot |\tilde{x} - x|
  • B: Die Basis der Maschinenzahl
  • e: Der Exponent der Maschinenzahl (Standard-Wert: 0)
  • n: Die Anzahl Stellen der Mantisse m
  • x: Der darzustellende Wert
  • \tilde{x}: Die Annäherung/Approximation an x
  • f: Auszuwertende Funktion

Konditionszahl

Die Konditionszahl gibt an, wie gross der potenzielle relative Fehler einer numerischen Lösung ist.

Eine niedrige Konditionszahl (K \le 1) bedeutet einen niedrigen Fehler, eine hohe Konditionszahl ein grosses Fehlerrisiko.

Formel:

Konditionszahl:

K = \frac{|f'(x)| \cdot |x|}{|f(x)|}

Nullstellenprobleme

Problemstellung und Ansatz

Es wird der korrekte Wert x für eine Aufgabe gesucht.

  1. Aufgabe ausformulieren:
    x = \sqrt{A}
  2. Aufgabe zu Nullstellenproblem umformulieren (Funktion, die bei gesuchtem x immer 0 ergibt): f(x) = x^2 - A
  3. (Algorithmisch) richtiges x finden, bei dem die Funktion 0 ergibt
  4. Das gefundene x ist die Lösung

Note:
Als Ausgangsbedingung für eine numerische Lösung eines Nullstellenproblems können diverse Bedingungen verwendet werden wie etwa:

  • Eine bestimmte Anzahl Iterationen
  • Abstand zwischen x_n und x_{n + 1} unterschreitet Threshold (approximiertes Resultat)
    • Ein niedriger Threshold ergibt ein genaueres Resultat
    • Ein Threshold von 0 ergibt das genaue Resultat

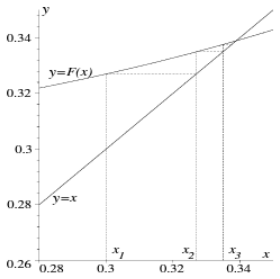
Fixpunktiteration

Ein möglicher Ansatz für ein solches Problem ist eine Fixpunktiteration.

Der Vorgang für eine solche ist folgende:

  1. Die Funktion in die Form F(x) = x.
    Beispiel für f(x) = x^2 - A:
    F(x) = \sqrt{A}
  2. Beliebigen Wert für x_0 wählen (vorzugsweise Wert in Nähe von erwarteter Lösung)
  3. Fixpunktiteration x_{n + 1} berechnen:
    x_{n+1} = F(x_n)

Dies wird durchgeführt bis die Ausgangsbedingung erfüllt ist.

Code-Beispiel:

import math

threshold = 10 ** -6

def f(x): # Funktion f in Nullstellenform
  return math.cos(x) - x

def F(x): # Funktion f in Fixpunktform
  return math.cos(x)

def F_(x): # Die Ableitung F'(x)
  return return -math.sin(x)

x = 0.75 # Startwert - angenommene, etwaige Lösung

if F_(x) >= 1:
  print("Fehler: Fixpunktiteration divergiert!")
else:
  while math.abs(x - F(x)) >= threshold:
    x = F(x)
  
  print(f"Approximierte Lösung: {x}")

Konvergenz

Eine Fixpunktiteration is konvergent (also berechenbar), wenn folgendes zutrifft:

|F'(\tilde{x})| < 1

Divergenz

Eine Fixpunktiteration is divergent (also unberechenbar), wenn folgendes zutrifft:

|F'(\tilde{x})| \ge 1
  • F(x): Die Fixpunktgleichung
  • F'(x): Die Ableitung der Fixpunktgleichung
  • x: Das genaue Resultat für x
  • \tilde{x}: Das approximierte Resultat für x (Fixpunkt)
  • x_n: Die $n$-te Approximation für x

Banachscher Fixpunktsatz

Der Fixpunktsatz dient dazu, abzuschätzen, wie gross der Fehler des Ergebnisses einer Fixpunktiteration in etwa ist.

Fixpunktsatz:

|F(x) - F(y)| \le \alpha \cdot |x - y| \text{für alle }x,y \in [a, b]

Alternative Umformung:

\frac{|F(x) - F(y)|}{|x - y|} \le \alpha

Fehlerabschätzung:

a-priori Abschätzung:

|x_n - \tilde{x}| \le \frac{\alpha^n}{1 - \alpha} \cdot |x_1 - x_0|

a-posteriori Abschätzung:

|x_n - \tilde{x}| \le \frac{\alpha}{1 - \alpha} \cdot |x_n - x_{n - 1}|

Konstante \alpha:

\alpha = \max_{x_0 \in [a, b]}| F'(x_0)|
\alpha \approx |F'(\tilde{x})|

Folgendermassen kann dieser aufgestellt werden:

Note:
In dieser Passage wird sowohl a (der Buchstabe "a") als auch \alpha (Alpha) verwendet. Diese haben hier eine unterschiedliche Bedeutung.

  1. Start- und Endpunkt a und b auswählen, welche genau einen Fixpunkt \tilde{x} beinhalten
  2. Prüfen, ob folgendes Zutrifft: Alle Ergebnisse von F([a, b]) befinden sich im Intervall [a, b]
  3. Konstante \alpha berechnen (gem. Formel)
  4. Die a-priori und die a-posteriori Abschätzung kann nun beliebig angewendet werden. Hierbei wird für x_0 der Wert a verwendet.

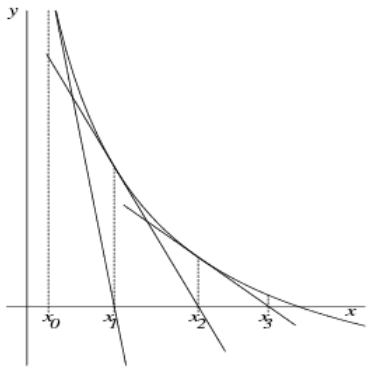
Newton-Verfahren

Das Newton-Verfahren erreicht die Konvergenz (d.h. das (approximierte) Resultat) um einiges schneller.

Hierfür wird die Funktion f in der Nullstellenform benötigt (f(x) = \text{[...]} = 0).

Newton-Verfahren:

x_{n + 1} = x_n - \frac{f(x_n)}{f'(x_n)}

Vereinfachtes Newton-Verfahren:

x_{n + 1} = x_n - \frac{f(x_n)}{f'(x_0)}

Konvergenz-Kontrolle:

\left|\frac{f(x) \cdot f''(x)}{(f'(x))^2}\right| < 1

Das Ergebnis ist wahr, wenn mit dem gewählten x eine Konvergenz erreicht werden kann.

  1. Startpunkt x_0 in der Nähe einer Nullstelle wählen
  2. (Wahlweise vereinfachtes) Newton-Verfahren anwenden bis x_n und x_{n + 1} bis Ausgangsbedingung erreicht wird

Sekantenverfahren

x_{n + 1} = x_n - \frac{x_n - x_{n - 1}}{f(x_n) - f(x_{n - 1})} \cdot f(x_n)

Vorgang:

  1. Startpunkte x_0 und x_1 wählen (Punkte, die eine Nullstelle umschliessen)
  2. Iteration durchführen, bis Ausgangsbedingung erfüllt wird

Konvergenz-Ordnung

Ein Verfahren hat eine Konvergenz-Ordnung q \ge 1, wenn es eine Konstante c > 0 für die für alle n Iterations-Schritte gilt:

|x_{n + 1} - \tilde{x}| \le c \cdot |x_n - \tilde{x}|^q
  • c: Beliebige Konstante
  • q: Konvergenz-Ordnung
    • Für Newton-Verfahren: q = 2
    • Für vereinfachtes Newton-Verfahren: q = 1
    • Für Sekanten-Verfahren: 1 = (1 + \sqrt{5}) : 2 \approx 1.618

Fehlerabschätzung

Wenn folgendes zutrifft:

f(x_n - \varepsilon) \cdot f(x_n + \varepsilon) < 0

Schneidet f zwischen x_n - \varepsilon und x_n + \varepsilon die Nullstelle.

Deswegen gilt folgendes:

|x_n - \xi| < \varepsilon

Sprich: Der Fehler ist kleiner als \varepsilon.

Vorgang:

  • \varepsilon suchen, für die oben genannte Bedingung zutrifft
  • Der maximale Fehler ist \varepsilon
  • x_n: Der approximierte $x$-Wert nach der $n$-ten Iteration
  • \varepsilon: Der maximale Fehler
  • \xi: Der Schnittpunkt der Nullstelle

Formelbuchstaben zu Nullstellenproblem

  • \alpha: Lipschitz-Konstante
  • [a, b]: Der
  • F(x): Die Fixpunktgleichung
  • F'(x): Die Ableitung der Fixpunktgleichung
  • x und y: Beliebig gewählte Punkte im Interval [a,b]
  • \tilde{x}: Das approximierte Resultat für x (Fixpunkt)
  • x_n Die $n$-te Approximation von x

Lineare Gleichungssysteme

Lernziele

  • Sie können...
    • Lineare Gleichungssysteme aufstellen
    • den Gauss-Algorithmus mit und ohne Pivotisierung
    • die LR-Zerlegung
    • die QR-Zerlegung
    • Jacobi-Verfahren (in Python)
    • Gauss-Seidel-Verfahren (in Python)
    • Fehlerabschätzungen
    • Eigenwerte und Eigenvektoren von Matrizen berechnen

Lineares Gleichungssystem:

Lineare Gleichungssysteme haben jeweils die Form A \cdot x = b wobei A und b gegeben und x gesucht ist:

$$A = \left( \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \ a_{21} & a_{22} & \cdots & a_{2n} \ \vdots & \vdots & & \vdots \ a_{n1} & a_{n2} & \cdots & a_{nn} \end{matrix} \right), x = \left( \begin{matrix} x_1 \ x_2 \ \vdots \ x_n \end{matrix} \right), b = \left( \begin{matrix} b_1 \ b_2 \ \vdots \ b_n \end{matrix} \right)

Eigenschaften

  • Gleich viele gesuchte Variablen x_n wie Gleichungen n. Folglich:
    • Die Matrix A ist eine quadratische Matrix mit Dimensionen n \times n
  • A ist invertierbar
  • A hat eine Determinante \det(A)

Dreiecks-Matrizen

L: Untere Dreiecksmatrix

Eine Matrix, die in der oberen rechten Ecke nur den Wert 0 und auf der Diagonale nur den Wert 1 hat. Eine Untere Dreiecksmatrix hat also folgende Form:

$$L = \left( \begin{matrix} 1 & 0 & 0 & \cdots & 0 \ l_{21} & 1 & 0 & \cdots & 0 \ l_{31} & l_{32} & 1 & \ddots & 0 \ \vdots & \vdots & \ddots & \ddots & 0 \ l_{n1} & l_{n2} & \cdots & l_{nn - 1} & 1 \end{matrix} \right)

R: Obere Dreiecksmatrix

Eine Matrix, die unten links von der Diagonale nur den Wert 0 beinhaltet. Eine Obere Dreiecksmatrix hat dementsprechend folgende Form:

$$R = \left( \begin{matrix} r_{11} & r_{12} & r_{13} & \cdots & r_{1n} \ 0 & r_{22} & r_{23} & \cdots & r_{2n} \ 0 & 0 & r_{33} & \cdots & r_{3n} \ \vdots & \vdots & \ddots & \ddots & \vdots \ 0 & 0 & \cdots & 0 & r_{nn} \end{matrix} \right)

Code-Beispiele:

Umwandlung in $R$-Matrix:

for i in range(n):
    if A[i, i] == 0:
        index = -1
        for j in range(i + 1, n):
            if A[j, i] > 0:
                index = j
        if index == -1:
            raise Exception("Invalid Matrix")
        else:
            # Swap lines
            A[[i, index]] = A[[index, i]]
    for j in range(i + 1, n):
        factor = A[j, i] / A[i, i]
        A[j] = A[j] - (factor * A[i])

Der Gauss-Algorithmus

Der Gauss-Algorithmus basiert darauf, dass ein lineares Gleichungssystem leicht lösbar ist, falls A eine obere Dreiecksmatrix ist. A muss also hierfür die Form einer oberen Dreiecksmatrix R haben.

Gauss-Algorithmus:

x_i = \frac{b_i - \sum_{j = i + 1}^n{a_{ij} \cdot x_j}}{a_{ii}}, i = n, n - 1, \dots, 1

Um den Gauss-Algorithmus anzuwenden, muss die Matrix A erst in eine $R$-Matrix umgewandelt werden. Dies funktioniert wie folgt:

  1. Mit i von 1 bis n
  2. Falls a_{ii} den Wert 0 hat:
    1. Mit j von i + 1 bis n
    2. Prüfen, ob a_{ji} einen höheren Wert als 0 hat
      • Falls Zeile gefunden wurde:
        • a_{i} mit a_{j} tauschen
        • b_{i} mit b_{j} tauschen
      • Sonst beenden: ungültige Matrix
  3. Mit j von i + 1 bis n
    1. a_k = a_k - \frac{a_{ki}}{a_{ii}} \cdot a_i
    2. b_k = b_k - \frac{a_{ki}}{a_{ii}} \cdot b_i

Code-Beispiel:

from numpy import array, zeros

def gaussMethod(A, b):
    A = array(A)
    n = A.shape[0]
    A = A.reshape((n, n))
    b = array(b).reshape((n))
    result = zeros(n)

    # Convert to R-Matrix
    for i in range(n):
        maxIndex = i
        for j in range(i + 1, n):
            if A[j, i] > A[maxIndex, i]:
                maxIndex = j
        # Swap lines
        A[[i, maxIndex]] = A[[maxIndex, i]]
        b[[i, maxIndex]] = b[[maxIndex, i]]
        for j in range(i + 1, n):
            factor = A[j, i] / A[i, i]
            A[j] = A[j] - (factor * A[i])
            b[j] = b[j] - (factor * b[i])
    # Calculate result
    for index in range(n, 0, -1):
        i = index - 1
        value = b[i]
        for j in range(i, n):
            value = value - A[i, j] * result[j]
        result[i] = value / A[i, i]
    return result.reshape((n, 1))

Fehlerfortpflanzung und Pivotisierung

  • Da beim Umwandeln einer Matrix A in die $R$-Form Zeilen in jedem Schritt mit dem Faktor \lambda = \frac{a_{ji}}{a_{ii}} multipliziert werden, vergrössert sich der Schritt immer um |\lambda|
  • \lambda kann klein gehalten werden, indem Zeilen der Grösse nach sortiert werden
  • In den Code-Beispielen ist dies bereits berücksichtigt

Determinanten-Bestimmung

Die Determinante einer Matrix A lässt sich einfach berechnen, sobald sie in die $R$-Form gebracht wurde mit folgender Formel:

Determinanten-Bestimmung mit Matrix \tilde{A} (die Matrix A in der $R$-Form):

$$\det(A) = (-1)^l \cdot \det(\tilde{A}) = (-1)^l \cdot \prod_{i = 1}^n{\tilde{a_{ii}}}

Code-Beispiel:

from numpy import array

def det(A):
    l = 0
    n = A.shape[0]
    A = A.reshape((n, n))

    # Convert to R-Matrix
    for i in range(n):
        maxIndex = i
        for j in range(i + 1, n):
            if A[j, i] > A[maxIndex, i]:
                maxIndex = j
        # Swap lines
        A[[i, maxIndex]] = A[[maxIndex, i]]
        l = l + 1
        for j in range(i + 1, n):
            factor = A[j, i] / A[i, i]
            A[j] = A[j] - (factor * A[i])

    result = 1
    for i in range(n):
        result = result * A[i, i]
    return (-1 ** l) * result

Die $LR$-Zerlegung

In der $LR$-Zerlegung wird die Matrix A in die Matrizen L und R aufgeteilt, sodass A = L \cdot R gilt.

Alternative Namen dieses Vorgangs sind $LR$-Faktorisierung und $LU$-decomposition.

Für in L und R zerlegte Matrizen gilt:

A \cdot x = b

und

A \cdot x = L \cdot R \cdot x = L \cdot y = b

Aufwand: Berechnung der $LR$-Zerlegung mit Gauss-Algorithmus benötigt ca. \frac{2}{3}n^3 Punktoperationen.

Falls Zeilenvertauschungen stattfinden, entsteht bei der $LR$-Zerlegung eine zusätzliche Permutations-Matrix P.

Für L und R zerlegte Matrizen mit Permutation P gilt:

P \cdot A = L \cdot R
L \cdot y = P \cdot b
R \cdot x = y

Das Verfahren für die $LR$-Zerlegung ist identisch zu den Schritten bei der Umwandlung in eine $R$-Matrix. Jedoch wird jeweils der Wert l_{ji} in der (zu Beginn) leeren Matrix L mit dem im aktuellen Eliminationsschritt gesetzt. Zudem muss bei Vertauschungen die Permutations-Matrix P entsprechend angepasst werden:

Code-Beispiel:

from numpy import array, identity, zeros

def decomposite(A):
    l = 0
    n = A.shape[0]
    R = A.reshape((n, n))
    L = zeros((n, n))
    P = identity((n, n))
    
    # Convert to LR-Matrix
    for i in range(n):
        maxIndex = i
        for j in range(i + 1, n):
            if A[j, i] > A[maxIndex, i]:
                maxIndex = j
        # Swap lines
        Pn = identity((n, n))
        A[[i, maxIndex]] = A[[maxIndex, i]]
        Pn[[i, maxIndex]] = Pn[[maxIndex, i]]
        P = P * Pn
        for j in range(i + 1, n):
            factor = R[j, i] / R[i, i]
            L[j, i] = factor
            R[j] = R[j] - (factor * R[i])

    result = 1
    for i in range(n):
        result = result * R[i, i]
    return [L, R, P]

Wenn die $LR$-Zerlegung, wie in diesem Code, Zeilenaustausch und das Berechnen von P involviert, spricht man von einer $LR$-Zerlegung mit Spaltenmaximum-Strategie.

Vorgang:

  1. Gemäss vorhergehender Beschreibung und Code-Beispiel die Matrizen L und R berechnen
  2. Mit Hilfe des Gauss-Algorithmus L \cdot y = P \cdot b nach y auflösen
  3. Mit Hilfe des Gauss-Algorithmus R \cdot x = y nach x auflösen

$QR$-Zerlegung

  • Die Matrix A wird in eine orthogonale Matrix Q und eine obere Dreiecksmatrix R zerlegt.
  • Orthogonal-Matrizen beschreiben Drehungen, Spiegelungen oder Kombinationen daraus.
  • Eine $QR$-Zerlegung erfordert ca. \frac{5}{3}n^3 Punktoperationen - ca. doppelt so viel wie die $LR$-Zerlegung.

Orthogonal-Matrix:

Eine Matrix Q ist orthogonal, wenn folgendes gilt:

Q^T \cdot Q = I_n

(x^T steht hierbei für eine Transformation)

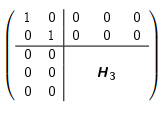
Housholder-Matrizen

Im Rahmen der Berechnung der Matrizen Q und R werden sogenannte "Housholder-Matrizen" berechnet.

Housholder-Matrizen:

Sei u ein Vektor mit beliebig vielen Dimensionen, für den gilt:

|u| = \sqrt{u_1^2 + u_2^2 + \dots + u_n^2} = 1

Die Householder-Matrix hat folgende Eigenschaft:

H := I_n - 2 \cdot u \cdot u^T

Für Housholder-Matrizen gilt zudem folgendes:

H = H^T = H^{-1}

und

H \cdot H = I_n

Berechnung einer Housholder-Matrix

Beispiel der Berechnung einer Housholder-Matrix zur ersten Spalte der Matrix A.

Für die Berechnung wird ein Einheitsvektor e benötigt, welcher genauso viele Werte hat, wie die Matrix Dimensionen. Ein Einheitsvektor hat im ersten Feld den Wert 1 und in allen anderen Feldern der Wert 0.

Für eine Matrix A mit der Dimension n = 3 lautet der Einheitsvektor e also wie folgt: $$e = \left(\begin{matrix} 1 \ 0 \ 0 \end{matrix}\right)

  1. Vektor v bestimmen 
    v = a_1 + sign(a_{11}) \cdot |a_1| \cdot e
  2. Vektor normieren: $$u = \frac{1}{|v|} \cdot v = \frac{1}{\sqrt{1^2 + 2^2 + 3^2}} \cdot \left(\begin{matrix} 1 \ 2 \ 3 \end{matrix}\right) = \frac{1}{\sqrt{14}} \cdot \left(\begin{matrix} 1 \ 2 \ 3 \end{matrix}\right)
  3. Die Housholder-Matrix H = I_n - 2 \cdot u \cdot u^T berechnen. $$H = \left(\begin{matrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \end{matrix}\right) - 2 \cdot \frac{1}{\sqrt{14}} \cdot \left(\begin{matrix} 1 \ 2 \ 3 \end{matrix}\right) \cdot \frac{1}{\sqrt{14}} \cdot \left(\begin{matrix} 1 & 2 & 3 \end{matrix}\right) \ H = \left(\begin{matrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \end{matrix}\right) - 2 \cdot \frac{1}{14} \cdot \left(\begin{matrix} 1 & 2 & 3 \ 2 & 4 & 6 \ 3 & 6 & 9 \end{matrix}\right) = -\frac{1}{7} \cdot \left(\begin{matrix} -6 & 2 & 3 \ 2 & -3 & 6 \ 3 & 6 & 2 \end{matrix}\right)
  • H: Housholder-Matrix
  • I: Identitäts-Matrix
  • n: Anzahl Dimensionen der Matrix

Vorgang

Im Rahmen des Vorgangs entspricht A_1 der Matrix A.

Die $QR$-Zerlegung kann folgendermassen durchgeführt werden:

  1. R = A
  2. Q = I_n
  3. Für i von 1 bis n - 1
    1. Gemäss vorheriger Anleitung Householder-Matrix H_i für die erste Spalte von A_i berechnen
    2. Householder-Matrix um Identitäts-Matrix erweitern. Beispiel:
    3. Erweiterte Householder-Matrix als Q_i speichern
    4. R = Q_i \cdot R
    5. Q = Q \cdot Q_i^T
    6. Die Gleichung R \cdot x = Q^T \cdot b mit Gauss-Algorithmus lösen

Code-Beispiel:

from numpy import array, identity, sign, sqrt, square, sum, zeros

def qrSolve(A, b):
    A = array(A)
    n = A.shape[0]
    R = A.reshape((n, n))
    Q = identity(n)

    for i in range(n - 1):
        I = identity(n - i)
        Qi = identity(n)
        e = zeros((n - i, 1))
        e[0][0] = 1
        a = R[i:,i:i + 1]
        v = a + sign(a[0]) * sqrt(sum(square(a))) * e
        u = (1 / sqrt(sum(square(v)))) * v
        H = I - 2 * u @ u.T
        Qi[i:,i:] = H
        R = Qi @ R
        Q = Q @ Qi.T
        R[i + 1:,i:i + 1] = zeros((n - (i + 1), 1))
    return linalg.solve(R, Q.T @ b)

Fehlerrechnung bei linearen Gleichungssystemen

Ähnlich wie herkömmliche Gleichungen, können Gleichungssysteme nicht mit eindeutiger Genauigkeit berechnet werden. Es entsteht ein Fehler.

Fehler bei linearen Gleichungssystemen:

A \cdot \tilde{x} = \tilde{b} = b + \Delta b
\Delta x = \tilde{x} - x
  • A: Matrix eines linearen Gleichungssystems
  • b: Gewünschtes Ergebnis des Gleichungssystems
  • \tilde{b}: Ergebnis des Gleichungssystems unter Verwendung von \tilde{x} in A \cdot \tilde{x}
  • \Delta b: Residuum: Die Differenz von b und \tilde{b}
  • x: Genaue Lösung
  • \tilde{x}: Näherungslösung von x
  • \Delta x: Der Fehler der Näherungslösung \tilde{x}

Vektor- und Matrixnormen

Vektornormen:

$1$-Norm, Summen-Norm:

||x||_1 = \sum_{i = 1}^n|x_i|

$2$-Norm, euklidische Norm:

||x||_2 = \sqrt{\sum_{i = 1}^n x_i^2}

$\infin$-Norm, Maximum-Norm:

||x||_\infin = \max_{i = 1, \dots, n}|x_i|

Matrixnormen:

$1$-Norm, Spaltensummen-Norm:

||A||_1 = \max_{j=1, \dots, n}\sum_{i = 1}^n|a_{ij}|

$2$-Norm, Spektral-Norm:

||A||_2 = \sqrt{\rho(A^T \cdot A)}

$\infin$-Norm, Zeilensummen-Norm:

||A||_\infin = \max_{i = 1, \dots, n}\sum_{j = 1}^n|a_{ij}|

Folgendes gilt für die Abschätzung von Vektoren und Matrizen:

Fehlerabschätzung von Vektoren und Matrizen:

Für die Gleichung A \cdot x = b und die dazugehörige Approximation A \cdot \tilde{x} = \tilde{b} gilt:

Absoluter Fehler:

||x - \tilde{x}|| \le ||A^{-1}|| \cdot ||b - \tilde{b}||

Falls ||b|| \not = 0 gilt zudem:

Relativer Fehler:

\frac{||x - \tilde{x}||}{||x||} \le ||A|| \cdot ||A^{-1}|| \cdot \frac{||b - \tilde{b}||}{||b||}

Konditionszahl:

Die Konditionszahl cond(A) einer Matrix A berechnet sich wie folgt:

cond(A) = ||A|| \cdot ||A^{-1}||

Eine hohe Konditionszahl cond(A) bedeutet, dass kleine Fehler im Vektor b zu grossen Fehlern im Ergebnis x führen können. In diesem Fall ist eine Matrix schlecht konditioniert.

Fehlerabschätzung von Matrizen mit Fehlern:

Sollte auch die Matrix A fehlerhaft sein (fehlerhafte Matrix \tilde{A}), gilt der nachstehende Satz unter folgender Bedingung:

cond(A) \cdot \frac{||A - \tilde{A}||}{||A||} < 1

dann gilt:

Relativer Fehler:

$$\frac{||x - \tilde{x}||}{||x||} \le \frac{cond(A)}{1 - cond(A) \cdot \frac{||A - \tilde{A}||}{||A||}} \cdot \left( \frac{||A - \tilde{A}||}{||A||} + \frac{||b - \tilde{b}||}{||b||} \right)

Aufwand-Abschätzung

Kennzahlen:

Lösung Linearer Gleichungssysteme mit Hilfe von...

Gauss-Elimination:

\frac{2}{3}n^3 + \frac{5}{2}n^2 - \frac{13}{6}n

$LR$-Zerlegung:

\frac{2}{3}n^3 + \frac{7}{2}n^2 + \frac{13}{6}n

$QR$-Zerlegung:

\frac{5}{3}n^3 + 4n^2 + \frac{7}{3}n - 7

Ordnung $O(n)$

Die Ordnung O(n) der zuvor genannten Verfahren entspricht der höchsten Potenz von n, welche in der Formel zur Berechnung des Aufwands vorkommt.

Das bedeutet also folgendes:

Ordnung von Gauss-Elimination, $LR$-Zerlegung und $QR$-Zerlegung:

O(n^3)

Iterative Verfahren zur Lösung von Gleichungssystemen

$LDR$-Zerlegung

Für die $LDR$-Zerlegung wird die Matrix A in drei Matrizen L, D und R aufgeteilt, wobei L eine untere Dreiecksmatrix, D eine Diagonalmatrix und R eine obere Dreiecksmatrix ist. Das bedeutet:

A = L + D + R

Mit

$$L = \left( \begin{matrix} 0 & 0 & 0 & \cdots & 0 \ a_{21} & 0 & 0 & \cdots & 0 \ a_{31} & a_{32} & 0 & \cdots & 0 \ \vdots & \vdots & \ddots & \ddots & \vdots \ a_{n1} & a_{n2} & \cdots & a_{nn - 1} & 0 \end{matrix} \right)$$ $$D = \left( \begin{matrix} a_{11} & 0 & 0 & \cdots & 0 \ 0 & a_{22} & 0 & \cdots & 0 \ 0 & 0 & a_{33} & \cdots & 0 \ \vdots & \vdots & \ddots & \ddots & \vdots \ 0 & 0 & \cdots & 0 & a_{nn} \end{matrix} \right)

$$R = \left( \begin{matrix} 0 & a_{12} & a_{13} & \cdots & a_{1n} \ 0 & 0 & a_{23} & \cdots & a_{2n} \ 0 & 0 & 0 & \ddots & \vdots \ \vdots & \vdots & \ddots & \ddots & a_{n-1,n} \ 0 & 0 & \cdots & 0 & 0 \end{matrix} \right)

Wichtig:
Hierbei handelt es sich nicht um L und R aus der $LR$-Zerlegung!

Jacobi-Verfahren

Das Jacobi-Verfahren ist ein iteratives Verfahren, welches nach jeder Iteration näher mit der tatsächlichen Lösung x konvergiert.

Das Jacobi-Verfahren ist auch bekannt als Gesamtschrittverfahren.

Jacobi-Verfahren:

Zunächst beginnt man mit x^{(0)} als ein Vektor, der nur aus $0$en besteht.

x^{(k + 1)} = -D^{-1} \cdot (L + R) \cdot x^{(k)} + D^{-1} \cdot b

Für die Berechnung einzelner Elemente des Vektors x^{(k + 1)} gilt:

Für i von 1 bis n:

$$x^{(k + 1)}i = \frac{1}{a{ii}} \cdot \left( b_i - \sum_{j = 1,j \not = i}^n a_{ij} \cdot x^{(k)}_j \right)

  • x^{(k)}: Die Annäherung an x nach der $k$-ten Iteration

Gauss-Seidel-Verfahren

Das Gauss-Seidel-Verfahren konvergiert schneller als das Jacobi-Verfahren.

Da für die Berechnung des Jacobi-Verfahrens für die Berechnung von x_2 auch Werte von x_1 verwendet werden, können die Werte direkt aus der aktuellen Iteration k wiederverwendet werden, um den Vorgang schneller konvergieren zu lassen.

Das Gauss-Seidel-Verfahren wird auch Einzelschrittverfahren genannt.

Gauss-Seidel-Verfahren:

x^(k+1) = -(D + L)^{-1} \cdot R \cdot x^{(k)} + (D + L)^{-1} \cdot b

Für die Berechnung einzelner Vektor-Komponente wiederum:

Für i von 1 bis n:

$$x^{(k + 1)}i = \frac{1}{a{ii}} \cdot \left( b_i - \sum_{j = 1}^{i - 1} a_{ij} \cdot x^{k + 1}j - \sum{j = i + 1}^n a_{ij} \cdot x^{(k)}_j \right)

Formelbuchstaben

  • \alpha: Lipschitz-Konstante (siehe Fixpunktsatz)
  • [a,b]: Das Untersuchungs-Interval für den Banachschen Fixpunktsatz
  • A: Matrix eines linearen Gleichungssystems
  • \tilde{A}: Umgewandelte Version der Matrix A
  • A^T: Transformierte Matrix A
  • b: Das gewünschte Resultat eines linearen Gleichungssystems
  • B: Basis der Maschinenzahl
  • e: Exponent der Maschinenzahl
  • H: Housholder-Matrix (siehe $QR$-Zerlegung)
  • I: Identitäts-Matrix (Matrix, überall den Wert 0 und auf der Diagonalen den Wert 1 hat)
  • K: Konditionszahl
  • L: Untere Dreiecksmatrix/Normierte Matrix
  • m: Mantisse (Darstellbarer Bereich der Maschinenzahl)
  • n: Anzahl möglicher Stellen der Mantisse m
  • q: Konvergenz-Ordnung
  • Q: Orthogonal-Matrix in der $QR$-Zerlegung
  • R: Obere Dreiecksmatrix
  • x: Darzustellender Wert
  • x_n: Die $n$-te Approximation von x
  • \tilde{x}: Approximation/Annäherung an x
  • x^{(k)}: Die Annäherung von x in der $k$-ten Iteration

Glossar