ZHAWNotes/Notes/Semester 3/STS - Stochastik und Statistik/Summary.md

Stochastik und Statistik

• Stochastik und Statistik
  • Deskriptive Statistik
    • Merkmals-Typen
    • Häufigkeiten
      • Klassierte Stichproben im Histogramm
    • Kennwerte
      • Quantile
      • Boxplot
      • Lage-Kennwerte
      • Streuungs-Kennwerte
      • Lagewerte in Klassierten Daten
• Glossar

Deskriptive Statistik

Ermittlung von Kenngrössen und Datenvalidierung

Merkmals-Typen

flowchart TD
  r[Merkmals-Typ]
  q[Qualitativ/Kategoriell]
  m[Quantitativ/Metrisch]
  n[Nominal]
  o[Ordinal]
  d[Diskret]
  s[Stetig]
  r --> q
  r --> m
  q --> n
  q --> o
  m --> d
  m --> s

• Qualitativ/Kategoriell - Unmessbar
  • Nominal: Nicht mit bestimmtem Wert verbunden
  • Ordinal: Mit Wert verbunden
• Quantitativ/Metrisch - Messbar
  • Diskret: Nur bestimmte Werte möglich
  • Stetig: Jegliche Werte möglich

Beispiele:

Frage: Welche Sprache sprichst du?

Ausprägungen	Merkmal-Typ
Deutsch, Französisch, Italienisch, Rätoromanisch	Nominal

Frage: Ich würde das Produkt weiterempfehlen

Ausprägungen	Merkmal-Typ
Stimme nicht zu, Stimme eher nicht zu, Keine Angabe, Stimme eher zu, Stimme zu	Ordinal

Frage: Wieviele Male hast du heute Steam gestartet?

Ausprägungen	Merkmal-Typ	Bemerkung
Ganze Zahlen > 0	Diskret	Es sind keine beliebigen Werte möglich (bspw. 0.5).

Frage: Was ist dein Welt-Rekord im 100-Meter-Lauf?

Ausprägungen	Merkmal-Typ	Bemerkung
Beliebige Zeit	Stetig	Jegliche Zahlen (mit beliebig vielen Kommastellen) sind möglich.

Frage: Wieviel kostet ein Mars-Riegel?

Ausprägungen	Merkmal-Typ	Bemerkung
Beliebiger Preis in CHF	Diskret	Beträge, die nicht durch 5 Rappen teilbar sind, sind nicht möglich.

Häufigkeiten

Eine Häufigkeit ist die Anzahl Male, die ein Merkmalsträger in der Stichprobe eine bestimmte Eigenschaft erfüllt. Diese kann auf verschiedene Weisen dargestellt werden.

• Absolute Häufigkeit h_i: Die absolute Häufigkeit ist die Anzahl der gezählten Elemente.
• Relative Häufigkeit f_i: Ergibt sich, indem man die absolute Häufigkeit durch den Stichproben-Umfang teilt.

  f_i = \frac{h_i}{n}

Zudem gelten folgende Regeln:

\sum_{i = 1}^n h_i = n

\sum_{i = 1}^n f_i = 1

Die Funktion für die Häufigkeitsfunktion (auch genannt: Dichtefunktion) hat folgende Abkürzungen:

• Für diskrete Merkmale: PMF (probability mass function)
• Für stetige Merkmale: PDF (probability density function)

Zudem gibt es folgende Verteilungsfunktionen:

• H(x) Absolute Summenhäufigkeit: Anzahl Merkmalträger mit Merkmal x_i mit x_i < x
• F(x) Kummulative Verteilungsfunktion CDF: Relative Häufigkeit der Merkmalträger mit Merkmal x_i mit x_i < x

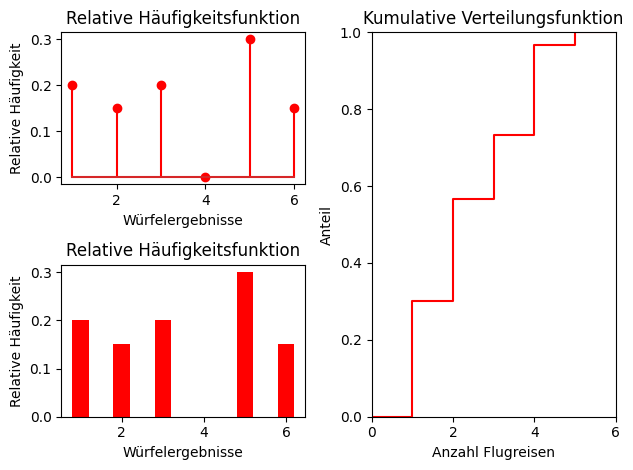
Beispiele der wichtigsten Häufigkeits-Funktionen:

• f_i: Relative Häufigkeit
• h_i: Absolute Häufigkeit
• n: Anzahl Merkmalträger in der Stichprobe

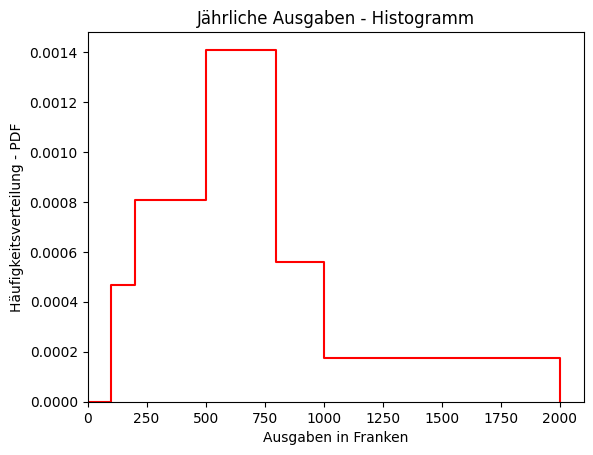
Klassierte Stichproben im Histogramm

Klassierte Stellen werden durch Grösse der Klasse geteilt, um diese zu berücksichtigen.

Daraus gewonnene Daten können in einem Histogramm dargestellt werden.

Beispiel:

Klasse	[100,200[	[200,500[	[500,800[	[800,1000[	[1000,2000[	Total
Absolute Häufigkeit	35	182	317	84	132	750
Relative Häufigkeit	\frac{35}{750}	\frac{182}{750}	\frac{317}{750}	\frac{84}{750}	\frac{132}{750}	1
Klassen-Grösse	100	300	300	200	1000
Säulenhöhe für Absolut	\frac{35}{100}	\frac{182}{300}	\frac{317}{300}	\frac{84}{200}	\frac{132}{1000}
Säulenhöhe für Relativ (PDF)	\frac{35}{750 \cdot 100}	\frac{182}{750 \cdot 300}	\frac{317}{750 \cdot 300}	\frac{84}{750 \cdot 200}	\frac{132}{750 \cdot 1000}

Histogramm der genannten Daten:

Kennwerte

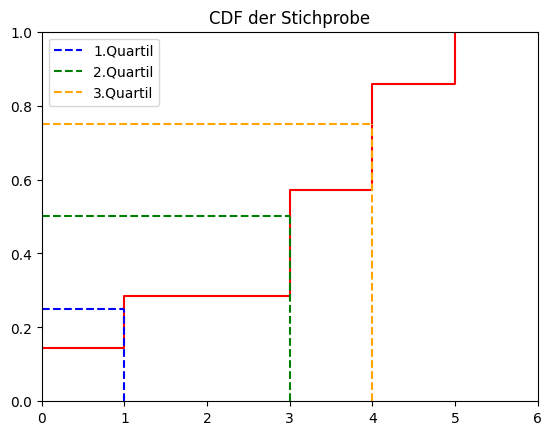
Quantile

Ein $q$-Quantil definiert den Wert des $\lceil n \cdot q \rceil$-te Element.

Folgende bekannte $q$-Quantile gibt es:

• $0.25$-Quantil: Das 1. Quartil
• $0.50$-Quantil: Das 2. Quartil auch "Median" oder "Zentralwert"
• $0.75$-Quantil: Das 3. Quartil

Beispiel einer Statistik mit eingezeichneten Quartilen:

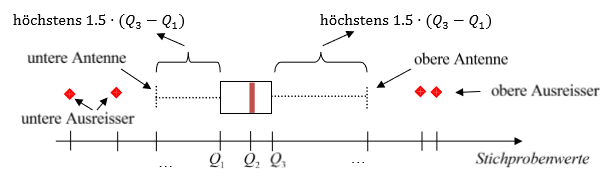
Boxplot

• Boxplots zeigen folgende Informationen
  • Das 1. Quartil Q_1
  • Den Median Q_2
  • Das 3. Quartil Q_3
  • Den Minimalwert (min. 1.5 \cdot (Q_3 - Q_1))
  • Den Maximalwert (max. 1.5 \cdot (Q_3 - Q_1))

Lage-Kennwerte

• Arithmetisches Mittel \overline{x}: Mittelwert der Stichprobenwerte
• Median x_\text{med}: Wert des 2. Quartil Q_2
• Modus x_\text{mod}: Der häufigste Wert in der Stichprobe

Streuungs-Kennwerte

Varianz \tilde{s}^2:

\tilde{s}^2 = \left(\frac{1}{n} \cdot \sum_{i = 1}^m{a_i^2 \cdot h_i}\right) - \tilde{x}^2

alternative Schreibweisen:

$$\begin{aligned} \tilde{s}^2 &= \frac{1}{n} \cdot \sum_{i = 1}^n(x_i - \overline{x})^2 = \frac{1}{n} \cdot \sum_{i = 1}^m{h_i \cdot (a_i - \overline{x})^2} \ &= \left(\frac{1}{n} \cdot \sum_{i = 1}^n x_i^2\right) - \overline{x}^2 = \left(\sum_{i = 1}^m{a_i^2 \cdot f_i}\right) - \overline{x}^2 \end{aligned}

Standardabweichung \tilde{s}:

\tilde{s} = \sqrt{\tilde{s}^2}

Korrigierte Varianz s^2:

s^2 = \frac{n}{n - 1} \tilde{s}^2

Korrigierte Standardabweichung s:

s = \sqrt{s^2} = \sqrt{\frac{n}{n - 1}} \cdot \tilde{s}

Interquartilsabstand IQR:

IQR = Q_3 - Q_1

• a_i: $i$-te Merkmals-Ausprägung
• m: Anzahl unterschiedlicher Merkmals-Ausprägungen (oder Klassen)

Lagewerte in Klassierten Daten

Einige Werte berechnen sich speziell in klassierten Daten.

Quantile:

Der Wert R_q eines $q$-Quantils berechnet sich, indem folgendes durchgeführt wird:

1. Erste Klasse K mit einem CDF > q finden
2. K_0 auf untere und K_1 auf obere Grenze der Klasse K setzen
3. Folgendes berechnen:

   R_q = K_0 + \frac{(K_1 - K_0) \cdot (q - CDF(K_0))}{CDF(K_1) - CDF(K_0)}

4. R_q entspricht nun dem $q$-Quartil

Modus:

1. Klasse K mit grösster relativer Häufigkeit bestimmen
2. K_0 auf untere und K_1 auf obere Grenze der Klasse K setzen
3. Folgendes berechnen:

   x_\text{mod} = K_0 + \frac{K_1 - K_0}{2}

Glossar

• Univariate Daten: Daten, welche nur ein Merkmal haben