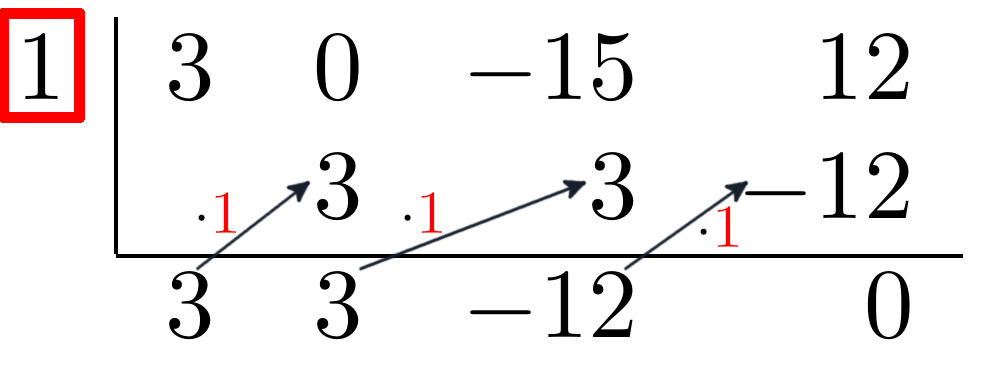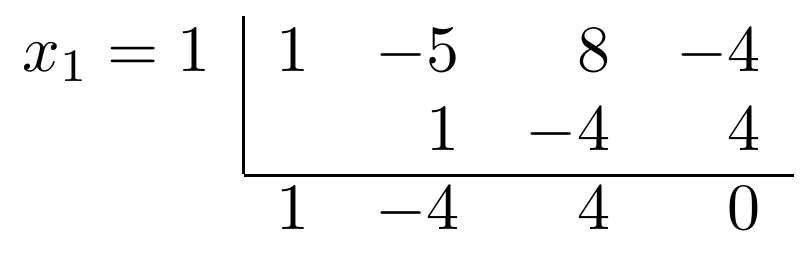ZHAWNotes/Notes/Semester 2/AN2 - Analysis 2/Zusammenfassung SEP.md

Zusammenfassung Analysis 2

Nullstellen durch Horner-Schema

Das Horner-Schema erlaubt es, Nullstellen leicht zu bestimmen.

Der Vorgang wird anhand der folgenden Gleichung aufgezeigt:

f(x) = 3x^3 - 15x + 12

Eine Nullstelle dieser Formel ist die 1. Dies lässt sich wie folgt mit dem Horner-Schema prüfen:

1. Nullstelle aufschreiben

Im Bild rot markiert

2. Die Koeffizienten aller $x$-Potenzen aufschreiben

Zu sehen im Bild in der obersten Reihe.
Entspricht eine der Koeffizienten 0 (wie in diesem Beispiel x^2), so muss im Horner-Schema eine 0 eingetragen werden.

4. Startwert notieren Die Berechnung wird gestartet indem man den ersten Koeffizient (in diesem Fall 3) in die unterste Reihe überträgt.

5. Berechnung

In diesem Schritt multipliziert man die Eingabe-Zahl mit der bekannten Nullstelle (im Bild durch graue Pfeile markiert) und addiert das Ergebnis mit dem nachfolgenden Koeffizienten.

Ist das letzte Resultat 0, so handelt es sich auch wirklich um eine Nullstelle.

Note:
Anhand der Resultat-Reihe im Horner-Schema lässt sich das übrigbleibende Polynom ablesen.

Rechnet man die Nullstelle 1 aus der Rechnung 3x^3 - 15x + 12 heraus, so würde das übrigbleibende Polynom folgendermassen lauten:

3x^2 + 3x - 12

Verdeutlicht:

3x^3 - 15x + 12 = (x - 1) \cdot (3x^2 + 3x - 12)

Stammfunktion

Umkehrung von Ableitungen gemäss der Seite über Ableitungen¹.

Alle Ableitungsregeln können unter Ableitungen nachgeschlagen werden.

Integrale

Integrale erlauben es, die Fläche unter Funktionen zu berechnen:

Beispiel anhand der Funktion $f(x) = x^3 + 5$

Integrale haben folgende Erscheinungsform:

\int_{a}^{b}{f(x)}dx

Die Zeichen haben folgende Bedeutung:

• \int: Integrations-Zeichen
• a: Die Untergrenze (Punkt ab dem integriert werden soll)
• b: Die Obergrenze (Punkt bis zu dem integriert werden soll)
• f(x): Zu integrierende Funktion
• dx: Bezeichnet, dass x integriert wird, indem unendlich kleine Rechtecke aufsummiert werden.

Grundintegrale

$$\begin{aligned} \int{a}dx &= ax \ \int{x^n}dx &= \frac{x^{n+1}}{n + 1}, &n &\not = -1 \ \int{\frac{1}{x}}dx &= \ln(|x|), &x &\not = 0 \ \int{a^x}dx &= \frac{a^x}{\ln(a)}, &a &> 0, &a &\not = 1 \end{aligned}

Integration von Produkten

Produkte benötigen zum Teil spezielle Vorgehensweisen um sie zu integrieren.

Zwei gängige Wege dazu sind im Folgenden Beschrieben.

Integration durch Substitution

Die Integration durch Substitution basiert auf der folgenden Regel:

\int_a^b{f(u(x)) \cdot u'(x)}dx = \int_{u(a)}^{u(b)}{f(u)}du

Die Integration durch Substitution wird hier anhand des folgenden Beispiels gezeigt:

\int_0^{\sqrt{\frac{\pi}{2}}}{\cos(x^2) \cdot x}dx

1. Funktionen bestimmen

Im Folgenden werden die Haupt- und die Unterfunktion bestimmt.

• u(x) = x^2
• g(x) = \cos(u)
• f(x) = g(u(x))

2. Substitutions-Gleichung für $dx$

Diese kann mit folgender Regel ermittelt werden:

\frac{du}{dx} = u'(x) \Rightarrow dx = \frac{du}{u'(x)}

Das ergibt in diesem Beispiel folgendes:

\frac{du}{dx} = u'(x) = 2x \Rightarrow dx = \frac{du}{2x}

3. Substitution

Nun müssen die errechneten Werte in die folgende Formel eingesetzt werden:

\int_{u(a)}^{u(b)}{f(u)}du

Wobei du durch unser errechnetes dx ersetzt werden muss.

Wichtig ist hierbei, dass sich x komplett wegkürzen lassen muss.

$$\int_0^{\sqrt{\frac{\pi}{2}}}{\cos(x^2) \cdot x}dx = \int_{u(0)}^{u(\sqrt{\frac{\pi}{2}})}{\cos(u) \cdot x \cdot \frac{du}{2x}}

Vereinfacht ergibt das folgendes:

\int_0^{\frac{\pi}{2}}{\frac{1}{2} \cdot \cos(u)}du = \left[\frac{1}{2} \cdot \sin(u)\right]_0^{\frac{\pi}{2}}

4. Resultat berechnen

\left[\frac{1}{2} \cdot \sin(u)\right]_0^{\frac{\pi}{2}} = \left(\frac{1}{2} \cdot 1\right) - \left(\frac{1}{2} \cdot 0\right) = \frac{1}{2}

Bei Integralen, die keine Grenzen definiert haben, lässt sich das Ergebnis nicht eindeutig bestimmen.

Hätte das ursprüngliche Integral keine Grenzen, wäre das Ergebnis folgendes:

\left[\frac{1}{2} \cdot \sin(u)\right] = \frac{1}{2} \cdot \sin(u) + C

5. Rücksubstitution

Im Falle eines Integrals ohne Grenzen muss die Variable u rück-substituiert werden:

\frac{1}{2} \cdot \sin(u) + C = \frac{1}{2} \cdot \sin(x^2) + C

Partielle Integration

Die Partielle Integration beruht auf folgender Regel:

\int_a^b{u'(x) \cdot v(x)dx} = \left[u(x) \cdot v(x)\right]_a^b - \int_a^b{u(x) \cdot v'(x)}dx

Die Partielle Integration wird anhand des folgenden Beispiels erklärt:

\int_0^\pi{sin(x) \cdot x}dx

Folgende Schritte müssen für die partielle Integration durchgeführt werden:

1. Unterfunktionen bestimmen

Einem Teil der Funktion v und einem anderen u' zuordnen. Sollte die partielle Integration nicht funktionieren, kann in diesem Schritt die Zuordnung von v und u' vertauscht werden.

• u'(x) = sin(x)
• v(x) = x

2. Stammfunktion von u' und Ableitung von v bestimmen

• u(x) = -\cos(x)
• v'(x) = 1

3. Resultat berechnen

Daraus ergibt sich folgende Gleichung:

\int_0^\pi{u'(x) \cdot v(x)dx} = \left[u(x) \cdot v(x)\right]_0^\pi - \int_0^\pi{u(x) \cdot v'(x)}dx

\left[-\cos(x) \cdot x\right]_0^\pi - \int_0^\pi{-\cos(x) \cdot 1}dx

((1 \cdot \pi) - (1 \cdot 0)) - \int_0^\pi{-\cos(x)}dx

(\pi - 0) - \left[\sin(x)\right]_0^\pi

(\pi - 0) - (\sin(0) - \sin(\pi))

(\pi - 0) - (0 - 0) = \pi

Note:
Die Partielle Integration kann auch für einfache Operationen verwendet werden, indem eine Multiplikation mit 1 durchgeführt wird.

Beispiel:

\int{ln(x)}dx = \int{ln(x) \cdot 1}dx

Partialbruchzerlegung

Für die Partialbruchzerlegung muss der zu integrierende Bruch vollständig gekürzt sein.

Die Partialbruchzerlegung wird anhand der folgenden Aufgabe erklärt:

\int{\frac{x + 1}{x^3 + 5x^2 + 8x - 4}}dx

Folgende Schritte müssen durchgeführt werden:

1. Nullstellen des Nenners bestimmen

Durch erraten: (Eine der Nullstellen ist 1)

Linearfaktor abspalten mit Horner-Schema:

Verbleibendes Polynom: x^2 - 4x + 4 = (x - 2) \cdot (x - 2)

Die verbleibende, doppelte Nullstelle ist also x = 2.

2. Jeder Nullstelle eine Summe von Nullstellen zuordnen

• Für einfache Nullstellen:

  \rightarrow \frac{A}{x - x_1}

• Für doppelte Nullstellen:

  \rightarrow \frac{A_1}{x - x_1} + \frac{A_2}{(x - x_1)^2}

• Für $r$-fache Nullstellen:

  \rightarrow \frac{A_1}{x - x_1} + \frac{A_2}{(x - x_1)^2} + ... + \frac{A_r}{(x - x_1)^r}

Das ergibt im Fall des Beispiels folgendes:

\frac{x + 1}{x^3 - 5x^2 + 8x - 4} = \frac{A}{x - 1} + \frac{B}{x - 2} + \frac{C}{(x - 2)^2}

3. Brüche gleichnamig machen

\frac{x + 1}{(x - 1)(x - 2)^2} = \frac{A(x - 2)^2}{(x + 1)(x - 2)^2} + \frac{B(x - 1)(x - 2)}{(x + 1)(x - 2)^2} + \frac{C(x - 1)}{(x + 1)(x - 2)^2}

Da die Brüche nun gleichnamig sind, können sämtliche Nenner weggekürzt werden:

x + 1 = A(x - 2)^2 + B(x - 1)(x - 2) + C(x - 1)

4. Koeffizienten mit Hilfe von LGS ausrechnen

Gleichung ausmultiplizieren und nach Potenz zerlegen:

(A + B)x^2 + (C - 4A - 3B)x + (4A + 2B - C)

• x + 1 beinhaltet kein x^2. Also muss (A + B) zwingend 0 ergeben:

  A + B = 0

• x + 1 beinhaltet 1x. Also muss C - 4A - 3B 1 ergeben:

  C - 4A - 3B = 1

• x + 1 beinhaltet eine Konstante 1. Also muss 4A + 2B - C 1 ergeben:

  4A + 2B - C = 1

Das Lösen des Gleichungssystems ergibt folgende Resultate:

• A = 2
• B = -2
• C = 3

Daraus ergibt sich folgendes:

\frac{x + 1}{(x - 1)(x - 2)^2} = \frac{2}{x - 1} + \frac{-2}{x - 2} + \frac{3}{(x - 2)^2}

5. Integration der Teilbrüche

Für Nenner ohne Exponent:

\int{\frac{1}{x - x_0}}dx = \int{\frac{1}{u}}du = \ln(|u|) + c = \ln(|x - x_0|) + c

Für Nenner mit Exponent: $$\begin{split} \int{\frac{1}{(x - x_0)^r}}dx = \int{u^{-r}}du & = \frac{u^{-r + 1}}{-r + 1} + c \ & = \frac{(x - x_0)^{-r + 1}}{1 - r} + c \ & = \frac{1}{(1 - r)(x - x_o)^{r - 1}} + c \end{split}

Für das aktuelle Beispiel ergibt das folgendes:

$$\begin{split} \int{\frac{2}{x - 1} + \frac{2}{x - 2} + \frac{3}{(x - 2)^2}}dx & = \int{\frac{2}{x - 1}} - \int{\frac{2}{x - 2}} + \int{\frac{3}{(x - 1)^2}} \ & = 2 \cdot \int{\frac{1}{x - 1} - 2 \cdot \int{\frac{1}{x - 2}}} + 3 \cdot \int{\frac{1}{(x - 2)^2}} \ & = 2 \cdot \ln(|x - 1|) - 2 \cdot \ln(|x - 2|) - 3 \cdot \frac{1}{x - 2} + c \end{split}

Leitfaden

Uneigentliche Integrale

Uneigentliche Integrale sind Integrale, welche einen unendlich grossen Integrationsbereich hat oder eine Polstelle (Grenze an unendlichem Wert) enthält.

Uneigentlicher Integrationsbereich

Dies ist der Fall, wenn die Untergrenze eines Integrals -\infin oder dessen Obergrenze +\infin ist.

Beispiel anhand des Integrals $\int_1^{\infin} 6 \cdot \frac{1}{x^2}$

Uneigentliche Integrale können berechnet werden, indem man erst die Stammfunktion ausformuliert, um dann den Grenzwert zu berechnen.

1. Bestimmung der Stammfunktion

\int_1^{\infin}{6 \cdot \frac{1}{x^2}} = \left[6 \cdot -\frac{1}{x}\right]_1^{\infin}

2. Grenzwert mit Hilfe von \lim berechnen

\left[6 \cdot -\frac{1}{x}\right]_1^{\infin} = 6 \cdot -\frac{1}{\infin} - 6 \cdot -\frac{1}{1} = 6 \cdot 0 - -6 \cdot -1 = 6

Differentialgleichungen

Gewöhnliche Differentialgleichungen

Differentialgleichungen sind Funktionen, welche als Rückgabewert an Stelle eines Skalar-Werts eine Funktion liefert.

Eine Differentialfunktion wird dargestellt durch die Ableitung, die resultierende Funktionen haben sollen:

So sind für die Differenzialgleichung y' = x - y + 1 alle resultierende Funktionen gültig, welche die Ableitung x - y + 1 haben.

Die Ordnung einer Differentialgleichung sagt aus, was der höchste Ordnung der höchsten vorkommenden Ableitung.

Differentialgleichungen 1. Ordnung

Differentialgleichungen 1. Ordnung lassen sich als Richtungsfelder darstellen:

Obig zu sehen ist das Richtungsfeld für die Differentialgleichung y' = x - y + 1.

Die Striche zeigen jeweils die Steigung, die das Resultate der Differentialgleichung mit dem entsprechenden $x$- und $y$-Wert hat.

Hierbei steht 0 für keine Steigung (waagerecht), -1 für eine 45°-Senkung nach unten und 1 für eine 45°-Steigung nach oben.

Alternativ lässt sich die Differentialgleichung auch in tabellarischer Form für y' darstellen:

f'(x_0, y_0)	x_0 = -3	x_0 = -2	x_0 = -1	x_0 = 0	x_0 = 1	x_0 = 2	x_0 = 3
y_0 = 2	-4	-3	-2	-1	0	1	2
y_0 = 1	-3	$-2	-1	0	1	2	3
y_0 = 0	-2	-1	0	1	2	3	4
y_0 = -1	-1	0	1	2	3	4	5
y_0 = -2	0	1	2	3	4	5	6

Euler-Schritte

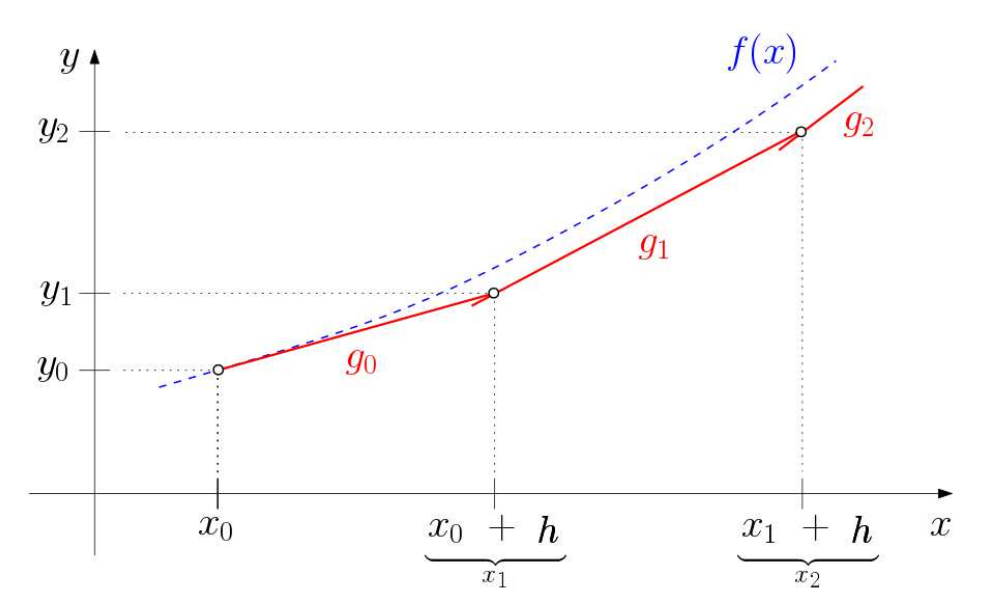
Ein Weg, um eine Lösung für eine Differentialgleichung zu approximieren ist die Methode der Euler-Schritte.

Beispiel mit folgenden Parametern:
y' = x + y, x_0 = 0, y_0 = 1, h = 1

Steigung Gerade	Berechnung	Beispiel
g_0\text{: } m_0 = F(x_0, y_0) = x_0 + y_0	x_1 = x_0 + h	= 0 + 1 = 1
Im Beispiel: 1	y_1 = y_0 + h \cdot F(x_0, y_0)	= 1 + 1 \cdot (0 + 1) = 2
g_1\text{: } m_1 = F(x_1, y_1) = x_1 + y_1	x_1 = x_0 + h	= 1 + 1 = 2
Im Beispiel: 3	y_1 = y_0 + h \cdot F(x_1, y_1)	= 2 + 1 \cdot (1 + 2) = 5
g_2\text{: } m_2 = F(x_2, y_2) = x_2 + y_2	x_3 = x_2 + h	= 2 + 1 = 3
Im Beispiel: 7	y_3 = y_2 + h \cdot F(x_2, y_2)	= 5 + 1 \cdot (2 + 5) = 12
etc.	etc.	etc.

Den Abstand zwischen den einzelnen Euler-Schritte h kann hierbei frei gewählt werden. Je kleiner h gewählt wird, desto genauer wird das Resultat.

Separierbare Differentialgleichungen

Definition

Eine Differentialgleichung 1. Ordnung ist _separierbar-, wenn sie sich in folgende Form bringen lässt:

y' = f(x) \cdot g(y)

Beispiele

• y' = (x^2 + \sin(x)) \cdot (e^y - y + 7) ist separierbar
• y' = x - y + 1 ist nicht separierbar

Lösungsweg

1. Gleichung zu Differentialquotient umschreiben:
   y' = \frac{dy}{dx} = f(x) \cdot g(y)
2. Trennung der Variablen:
   \frac{dy}{g(y)} = f(x) \cdot dx
3. Integration auf beiden Seiten der Gleichung:
   \int{\frac{dy}{g(y)} = \int{f(x) \cdot dx}}
4. Auflösen nach y

Beispiel

y' = k \cdot y

1. Gleichung zu Differentialquotient umschreiben:

y' = \frac{dy}{dx} = \underbrace{k}_{f(x)} \cdot \underbrace{y}_{g(y)}

2. Trennung der Variablen:

Alle x und y auf separate Seite des = bringen:

\frac{dy}{y} = k \cdot dx

3. Integration auf beiden Seiten der Gleichung:

$$\int{\frac{dy}{y}} = \int{\frac{1}{y}}dy = \ln(|y|) \ \int{k \cdot dx} = k \cdot x + C \ \ln(|y|) = k \cdot x + C$$

4. Auflösen nach y:

$$\ln(|y|) = k \cdot x + C \ |y| = e^{k \cdot x + C} \ y = \pm e^{k \cdot x + C} = \underbrace{\pm e^C}_{a} \cdot e^{k \cdot x} = a \cdot e^{k \cdot x}

Kontrolle:

$$y' = (a \cdot e^{k \cdot x})' = a \cdot k \cdot e^{k \cdot x} \ k \cdot y = k \cdot a \cdot e^{k \cdot x} \ y' = k \cdot y$$

Autonome Differentialgleichung

Als autonom werden die Differentialgleichungen bezeichnet, die sich in folgende Form bringen lassen:

y' = f(y)

Beispiele

Gleichung	Autonom?
y' = y^2 + 6	Ja
y' = x + y	Nein
y' = \frac{y}{x}	Nein
y' = y^2 \cdot \sqrt{1 - \sin(y)} - \ln(y)	Ja

Lösungsweg

Gleich wie separierbare Differentialgleichungen.

---

1. Ableitungen ↩︎