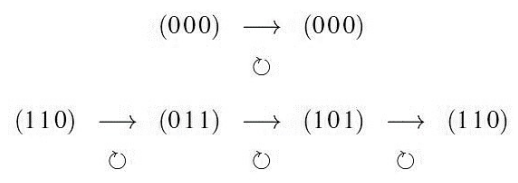38 KiB
| Footer | Header | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
Zusammenfassung INCO
Inhaltsverzeichnis
- Zusammenfassung INCO
- Inhaltsverzeichnis
- Formeln
- Zahlensysteme
- Informationstheorie
- Quellencodierung
- Audiocodierung
- Kanalcodierung
- Fehlererkennung
- Fehlerkorrektur
- Faltungscode
- Glossar
Formeln
Zahlensysteme
Zahlen berechnen
Beispiel anhand des $8$er- (Oktal)-Systems:
8^38^28^18^062576257_8 =6 \cdot 8^3 + 2 \cdot 8^2 + 5 \cdot 8^1 + 7 \cdot 8^0 =6 \cdot 512 + 2 \cdot 64 + 5 \cdot 8 + 7 \cdot 1 =3072 + 128 + 40 + 8 = 3248
Hex \Leftrightarrow Bin
| Hex | Bin |
|---|---|
0 |
0000 |
1 |
0001 |
2 |
0010 |
3 |
0011 |
4 |
0100 |
5 |
0101 |
6 |
0110 |
7 |
0111 |
8 |
1000 |
9 |
1001 |
A |
1010 |
B |
1011 |
C |
1100 |
D |
1101 |
E |
1110 |
F |
1111 |
Rechen-Operationen
Operationen werden generell identisch zu den herkömmlichen schriftlichen Rechenoperationen durchgeführt.
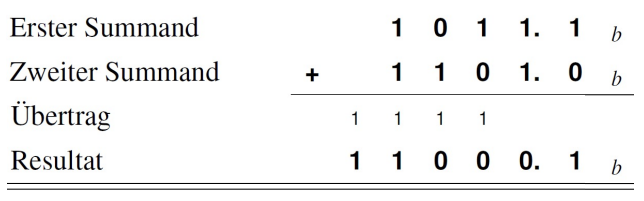
Addition
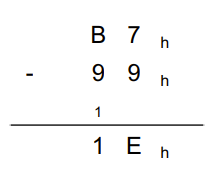
Subtraktion
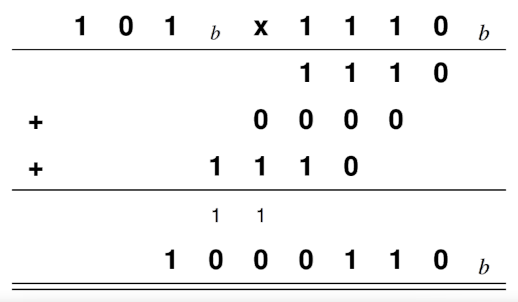
Multiplikation
Division
Darstellung von Negativen Zahlen
$1$er-Komplement
Das $1$er-Komplement wird gebildet indem man jede Ziffer einer Zahl durch die Ergänzung auf 1 ersetzt:
| Ursprüngliche Zahl | 0010 |
|---|---|
| Subtrahend | 1111 |
| $1$er-Komplement | 1101 |
Genauso kann für Dezimal-Zahlen ein $9$er-Komplement gebildet werden, indem alle Ziffern mit der Ergänzung auf 9 ersetzt werden:

Das Problem des $1$er-Komplements ist, dass 0 zwei verschiedene Darstellungsweisen hat.
Das $1$er-Komplement von 0 lautet nämlich folgendermassen:
| Ursprüngliche Zahl | 0000 |
|---|---|
| Subtrahend | 1111 |
| $1$er-Komplement | 1111 |
Die 0 kann also mit dem $1$er-Komplement sowohl als 0000 als auch als 1111 dargestellt werden.
$2$er-Komplement
Das $2$er-Komplement schafft hierbei Abhilfe und wird gebildet, indem man das $1$er-Komplement um 1 erhöht:
| Ursprüngliche Zahl | 0010 |
|---|---|
| Subtrahend | 1111 |
| $1$er-Komplement | 1101 |
| Summand | 0001 |
| $2$er-Komplement | 1110 |
So ergibt die Bildung des Komplements von 0 folgendes:
| Ursprüngliche Zahl | 0000 |
|---|---|
| Subtrahend | 1111 |
| $1$er-Komplement | 1111 |
| Summand | 0001 |
| $2$er-Komplement | 0000 |
Informationstheorie
Formeln
Probability P(x)
Die Wahrscheinlichkeit errechnet sich indem man die Anzahl Vorkommen des Symbols (N_x) durch die gesamte Anzahl Symbole in der Nachricht (N) teilt:
P(x) = \frac{N_x}{N}Beispiel:
Für ein Symbol, das $2$-mal in einer Nachricht mit4Symbolen vorkommt, würde die Rechnung also folgendermassen aussehen:P(x) = \frac{N_x}{N} = \frac{2}{4} = \frac{1}{2} = 0.5
Informationsgehalt I(x)
Der Informationsgehalt errechnet sich, indem man berechnet, wieviele Bits mindestens benötigt werden, um das Symbol x darzustellen.
Je weniger man ein Symbol in einer Nachricht erwartet, desto höher ist dessen Informationsgehalt.
I(x) = \log_2\left(\frac{1}{P(x)}\right)Entropie H(x)
Die Entropie besagt, was der durchschnittliche Informationsgehalt einer Datenquelle ist.
Die Entropie eines einzelnen Symbols oder eines einzelnen Falls errechnet sich wie folgt:
H(x) = P(x) \cdot \log_2\left(\frac{1}{P(x)}\right)Folgendermassen errechnet sich die Entropie einer ganzen Datenquelle:
H(x) = \sum^{N-1}_{n=1}\left(P(x_n) \cdot \log_2\left(\frac{1}{P(x_n)}\right)\right)Je gleichmässiger die Häufigkeit der einzelnen Symbole, desto höher die Entropie.
Die untenstehende Grafik zeigt das Verhältnis zwischen der Wahrscheinlichkeit in einem BMS (Binary Memoryless Source) und der daraus resultierenden Entropie.
Wie zu sehen ist die Entropie am höchsten, wenn die Wahrscheinlichkeit für $1$en (P(1)) identisch mit der Wahrscheinlichkeit für $0$en (P(0)) ist.
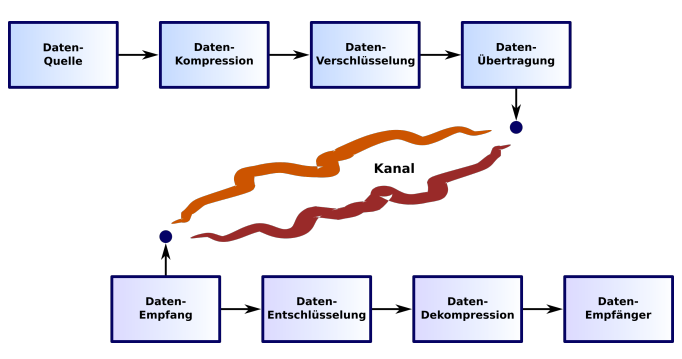
Quellencodierung
Unter Quellencodierung versteht man die Aufbereitung von Daten für einen optimierten Versand.
Grundsätze
Die Grundsätze und/oder Ziele der Quellencodierung sind folgende:
- Speicherplatz sparen
- Bandbreite reduzieren
- Kosten minimieren
- Übertragungszeit reduzieren
- Energie sparen
- Optimierung zwischen Verarbeitung und Übertragung
Folgendes sind keine Ziele der Quellencodierung
Datenverschlüsselung (Chiffrierung, Security)Sicherung der Datenintegrität durch Fehlererkennung und Fehlerkorrektur (folgt später, siehe Kanalcodierung)
Übersicht
- Die Irrelevanz-Reduktion ist darauf ausgelegt, Daten zu entfernen, die für den Empfänger irrelevant sind
- Nicht-hörbare Frequenzen bspw. in Musik
- Überhöhte, nicht wahrnehmbare Bildwiederholfrequenz
- Nicht wahrnehmbare Farben in Bildern
- Die Reduktion von Redundanz beschreibt die das verlustfreie Komprimieren von Daten
Formeln
Mittlere Symbollänge L(x)
L(x) = \sum_{n=0}^{N - 1} P(x_n) \cdot l_nEinheit: $\frac{Bit}{Symbol}$
Redundanz einer Codierung R(x)
R(x) = L(x) - H(x)Einheit: $\frac{Bit}{Symbol}$
Falls die Entropie einer Datenquelle grösser ist als die durchschnittliche Länge der codierten Worte, handelt es sich bei der Codierung um eine verlustbehaftete Kompression.
Run Length Encoding RLE
Die Lauflängencodierung ist die simpelste Art von Komprimierung.
Diese basiert auf das Prinzip, sich wiederholende Frequenzen in der Form [Marker, Anzahl, Symbol] festzuhalten.
Die Anzahl Bits, welche für da Speichern der Anzahl aufgewendet werden, sollte so gewählt werden, dass die typische Länge von RLE-Blöcken abgebildet werden kann.
Tritt also ein Symbol sehr oft hintereinander auf: ABBBBBBBBBA
Könnte diese beispielsweise in der folgenden Form dargestellt werden: AC9BA
C wird an dieser Stelle als RLE-Marker (Segment, welche den Start eines RLE-Codes markiert) eingesetzt.
Beispiel:
In diesem Code wird von einem System ausgegangen, welches nur die Übertragung vonT,E,R,A,U,I,W,Q,C,SundLzulässt.
- Quelle:
TERRRRRRRRRMAUIIIIIIIIIIIIIIIIIWQCSSSSSSSSSSLAls
RLE-Marker sollte das Symbol verwendet werden, das am allerwenigsten vorkommt (in diesem Fall wäre dasA). Da sich in der Quelle Symbole teils 10-17 Mal wiederholen werden für das Speichern derAnzahl2 Dezimalstellen (oder 5 Bits) verwendet:
RLE-komprimiert:
TEA09RMA01AUA17IWQCA10SL
Huffman Code
Der Huffman Code ermöglicht es einem, Codeworte zu generieren, welche folgende wichtige Grundsätze einhalten:
- Häufige Symbole haben kurze Code-Worte
- Seltene Symbole haben lange Code-Worte
- Präfix-frei
- Optimal (kein besserer, Präfix-freier Code möglich)
Schritte zum Bilden eines Huffman-Codes
- Alle Symbole aufsteigend nach Wahrscheinlichkeit
P(x)auflisten - dies sind die Blätter des Huffman-Baums - Entsprechende Wahrscheinlichkeiten dazuschreiben
- Blätter mit der kleinsten Wahrscheinlichkeit verbinden und die Summe der Wahrscheinlichkeiten in der entstehenden Gabelung notieren
- Punkt 3 Wiederholen bis alle Blätter miteinander verbunden sind
- Festlegen, welche Richtung des Astes einer Gabelung einer
0oder einer1entspricht - Entstehende Code-Werte notieren
Beispiel:
Beispiel anhand vonM,N,O,R,Smit folgenden Wahrscheinlichkeiten:P(M) = 0.35,P(N) = 0.2,P(O) = 0.25,P(R) = 0.05,P(S) = 0.15flowchart LR r["R (111)"]---4((0.05)) s["S (110)"]---5((0.15)) n["N (10)"]---1((0.2)) p["O (01)"]---2((0.25)) m["M (00)"]---3((0.35)) a1((0.2)) 4---a1 5---a1 b1((0.4)) a1---b1 1---b1 a2((0.6)) 2---a2 3---a2 c1((1.0)) b1---c1 a2---c1In diesem Beispiel wird die Richtungszuweisung
\uparrow = 1und\downarrow = 0verwendet.
LZ77-Kompression
Im LZ77-Verfahren werden die Daten durch ein Sliding Window bestehend aus Such- und Vorschau-Buffer geleitet, um diese nach Gemeinsamkeiten abzutasten:
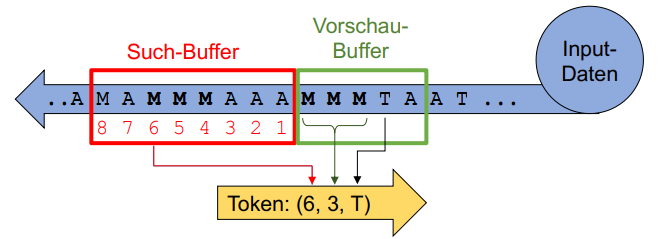
Wie in der Abbildung zu sehen wird der Vorschau-Buffer nach Übereinstimmungen im Such-Buffer geprüft.
Folgend ein Beispiel des Vorgangs einer LZ77-Kompression mit der Eingabe AMAMMMAAAMMMTAAT mit einer Such-Buffer Länge von 8 und einer Vorschau-Buffer Länge von 5:
| Such-Buffer | Vorschau-Buffer | Input-Daten | Token (Offset, Länge, Zeichen) |
|---|---|---|---|
AMAMM |
MAAAMMMTAAT |
(0, 0, A) |
|
A |
MAMMM |
AAAMMMTAAT |
(0, 0, M) |
AM |
AMMMA |
AAMMMTAAT |
(2, 2, M) |
AMAMM |
MAAAM |
MMTAAT |
(4, 2, A) |
AMAMMMAA |
AMMMT |
AAT |
(6, 4, T) |
MMAAAMMT |
AAT |
(6, 2, T) |
Bei der Decodierung werden die Token interpretiert und dessen Resultat am Ende des Buffers hinzugefügt. So werden redundante Daten automatisch wiederhergestellt.
| Token | Resultierender Buffer |
|---|---|
(0, 0, A) |
A |
(0, 0, M) |
AM |
(2, 2, M) |
AMAMM |
(4, 2, A) |
AMAMMMAA |
(6, 4, T) |
AMAMMMAAAMMMT |
(6, 2, T) |
AMAMMMAAAMMMTAAT |
LZW-Kompression
Das LZW-Verfahren lehnt nur geringfügig an dem LZ77-Verfahren an. An Stelle eines Sliding-Windows wird ein Wörterbuch verwendet.
Das Wörterbuch hat zu Beginn des Kompression lediglich 255 Einträge mit den dazugehörigen ASCII-Charakteren.
Während der Kompression wird das Wörterbuch nach und nach aufgebaut, neue Wörterbuch-Einträge werden als Token versendet. Ein Token besteht aus dem Index eines übereinstimmenden Wörterbuch-Eintrags, welches möglichst viele Zeichen lang ist.
Der Wert des Tokens setzt sich aus dem Wert des verwiesenen Wörterbuch-Eintrags und dem ersten Zeichen des Werts des nächsten Tokens zusammen:
Folgend ein Beispiel anhand des zu komprimierenden Wertes: AMAMMMAAAMMMTAAT:
| Input-Daten | Token-Index | Token | Wert |
|---|---|---|---|
AMAMMMAAAMMMTAAT |
256 |
65 |
AM |
MAMMMAAAMMMTAAT |
257 |
77 |
MA |
AMMMAAAMMMTAAT |
258 |
256 |
AMM |
MMAAAMMMTAAT |
259 |
77 |
MM |
MAAAMMMTAAT |
260 |
257 |
MAA |
AAMMMTAAT |
261 |
65 |
AA |
AMMMTAAT |
262 |
258 |
AMMM |
MTAAT |
263 |
77 |
MT |
TAAT |
264 |
84 |
TA |
AAT |
265 |
261 |
AAT |
T |
266 |
84 |
T |
Gesendet werden also folgende Daten:
[65, 77, 256, 77, 257, 65, 258, 77, 84, 261, 84]
Hinweis:
65ist der ASCII-Wert von einemA,77entspricht einemMund84einemT.
Für die Decodierung werden die versendeten Wörterbuch-Einträge wieder zu eigentlichem Text umgewandelt:
| Index | Token | Wert | Resultierender Buffer |
|---|---|---|---|
256 |
65 |
A? |
A |
257 |
77 |
M? |
AM |
258 |
256 |
AM? |
AMAM |
259 |
77 |
M? |
AMAMM |
260 |
257 |
MA |
AMAMMMA |
261 |
65 |
A? |
AMAMMMAA |
262 |
258 |
AMM? |
AMAMMMAAAMM |
263 |
77 |
M? |
AMAMMMAAAMMM |
264 |
84 |
T? |
AMAMMMAAAMMMT |
265 |
261 |
AA? |
AMAMMMAAAMMMTAA |
266 |
84 |
T |
AMAMMMAAAMMMTAAT |
JPEG-Kompressionsverfahren
JPEG ist eine verlustbehaftete Kompressionsart. Es gibt auch die Möglichkeit, Bilder verlustfrei mit JPEG zu komprimieren, diese Möglichkeit ist aber in kaum einem Programm vorzufinden. Diese entfernt sowohl Redundanz als auch Bild-Informationen (Farben), welche für das menschliche Auge kaum ersichtlich sind.
JPEG eignet sich vor allem bei Fotografien, während es für Dokumente oder Computergrafiken (aka. Bilder mit scharfen Kanten wie Schriften oder Website-Banner) nicht geeignet ist.
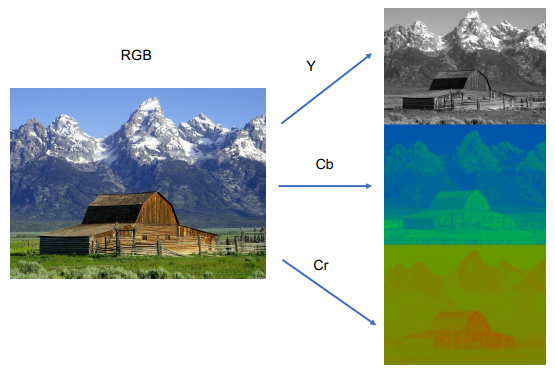
Aufteilung in Luminanz und Chrominanz
In einem ersten Schritt werden die Farbinformationen aufgeteilt in Luminanz Y, Chrominanz (Rot) C_R und Chrominanz (Blau) C_B.
Dieser Schritt ist notwendig, da das menschliche Auge viel affiner auf Helligkeit (die Luminanz) als auf Farben ist.
Der Schritt der Umwandlung von RGB in LCrCb ist verlustfrei.
Folgende Abbildung zeigt diese Umwandlung:
Die folgende Abbildung zeigt auf, wie die Farbwerte eines Bildes zu Luminanz-Werten umgerechnet werden können:
Mit Hilfe folgender Formel können aus RGB-Werten die dazugehörigen Luminanz und Chrominanz-Werte berechnet werden:
$$\begin{bmatrix}
Y \
C_B \
C_R
\end{bmatrix} =
\begin{bmatrix}
0.299 & 0.587 & 0.114 \
-0.1687 & -0.3313 & 0.5 \
0.5 & -0.4187 & -0.0813
\end{bmatrix}
\cdot
\begin{bmatrix}
R \
G \
B
\end{bmatrix}
+
\begin{bmatrix}
0 \
128 \
128
\end{bmatrix}
Erinnerung:
Im einzelnen bedeutet das bspw. folgendes:Y = (0.299 \cdot R + 0.587 \cdot G + 0.114 \cdot 0.114) + 0C_B = (-0.1687 \cdot R + -0.3313 \cdot G + 0.5 \cdot B) + 128C_R = (0.5 \cdot R + -0.4187 \cdot G + -0.0813 \cdot B) + 128
Die Formel zum Umwandeln von Luminanz- und Chrominanz-Werten lautet wie folgt:
$$\begin{bmatrix}
R \
G \
B
\end{bmatrix} =
\begin{bmatrix}
1 & 0 & 1.402 \
1 & -0.34414 & -0.71414 \
1 & 1.772 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
Y \
C_B - 128 \
C_R - 128
\end{bmatrix}
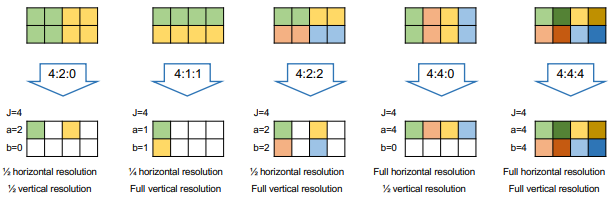
Downsampling
Da, wie bereits erwähnt, das Auge sensitiver auf Helligkeit (Luminanz) als auf Farben (Chrominanz) ist, kann die Auflösung der Chrominanz-Werte beliebig verringert werden.
Das Downsampling wird im Format J:a:b definiert.
Jsteht für die Breite der 2px hohen Blöckeasteht für die Anzahl Pixel nach dem Down-Sampling in der 1. Zeilebsteht für die Anzahl Pixel nach dem Down-Sampling in der 2. Zeile
Folgend einige Beispiele:
Nach dem Downsampling sehen die Bilder jeweils folgendermassen aus:
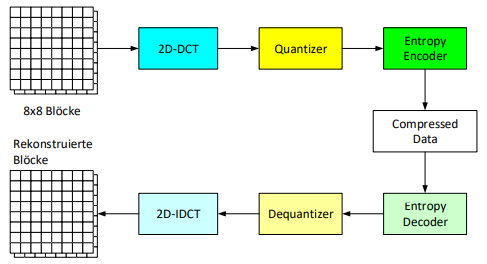
Block-Verarbeitung
Die hier geschilderten Schritte werden jeweils für Blöcke à 8x8 Pixel angewendet. Folgend ein Überblick über die einzelnen Schritte:
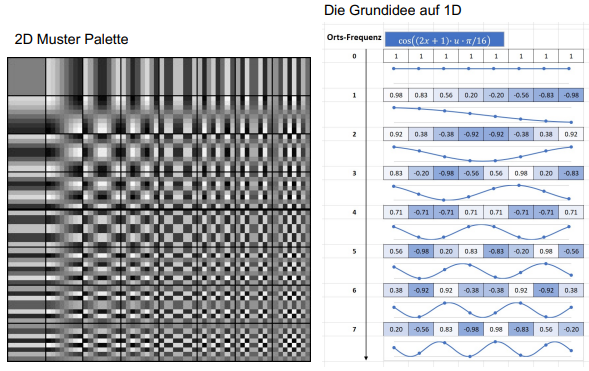
Diskrete Kosinus Transformation
Bei der Transformation werden die Werte in den 8x8-Blöcken (Werte von 0 bis 254) umgewandelt, sodass sie nicht mehr Koordinaten und die dazugehörigen Werte repräsentieren, sondern eine Gewichtung, wie sehr sie aus dem Muster einer bestimmten Kosinus-Frequenz zusammengesetzt sind:
Dies geschieht mit Hilfe folgender Formel:
F_{vu} = \frac{1}{4} \cdot C_u \cdot C_v \cdot \sum_{x=0}^7\sum_{y=0}^7B_{xy} \cdot \cos\left(\frac{(2x + 1) \cdot u \cdot \pi}{16}\right) \cdot \cos\left(\frac{(2y + 1) \cdot v \cdot \pi}{16}\right)Information:
C_u,C_v = \frac{1}{\sqrt{2}}füru=0oderv=0
C_u,C_v = 1für alle anderen Fälle (i.e.u \not =0undv \not = 0)
Folgendermassen lässt sich diese Formel auch wieder umkehren:
B_{yx} = \frac{1}{4}\sum_{u=0}^7\sum_{v=0}^7 C_u \cdot C_v \cdot F_{vu} \cdot \cos\left(\frac{(2x + 1) \cdot u \cdot \pi}{16}\right) \cdot \cos\left(\frac{(2y + 1) \cdot v \cdot \pi}{16}\right)Quantisierung
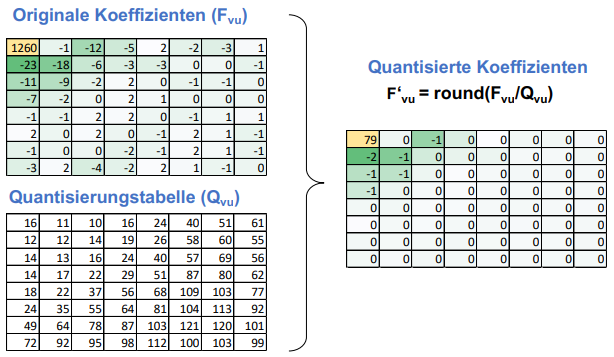
Die gewonnene 8x8 Frequenz-Tabellen werden anschliessend quantisiert. In diesem Schritt werden aufgrund einer Quantisierungstabelle (welche Resultat intensiver Experimente war) alle Werte dividiert.
Dies führt dazu, dass vorwiegend nur signifikante Werte in der rechten oberen Ecke übrig bleiben:
Entropy Encoding
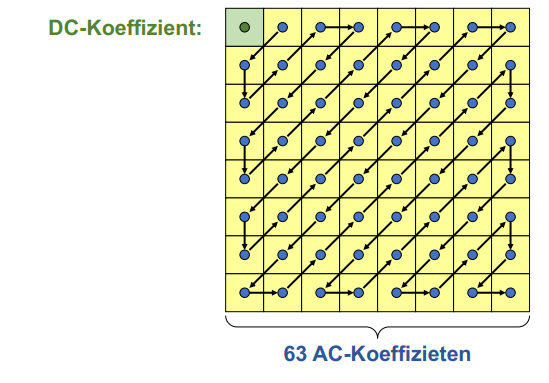
In einem letzten Schritt werden der DC-Koeffizient (Wert ganz oben links) und die AC-Koeffizienten (alle übrigen Werte) mit Hilfe von Run Length Encoding (siehe RLE) in der Form [DC-Wert, [Anzahl Nullen, Koeffizient]*, EOB] gespeichert.
Der "End of Block" (EOB) Marker markiert hierbei die Stelle ab der nur noch $0$-Werte folgen. Die Werte werden in einer diagonalen "Zick-Zack" Form abgetastet:
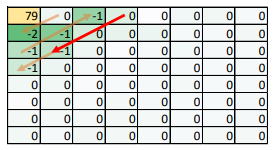
Die in dieser Abbildung ersichtlichen Werte würden also folgendermassen codiert werden:
(79), (1, -2), (0, -1), (0, -1), (2, -1), (0, -1), (EOB)
Qualitätsunterschied
Folgendes Beispiel zeigt, wie sich JPEG-Bilder je nach gewählter Qualität unterscheiden.
Audiocodierung
Im Folgenden ist beschrieben, wie die Audiocodierung im Wave-Format funktioniert.
Abtasttheorem
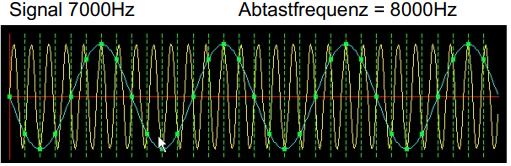
Um ein Audiosignal korrekt abtasten zu können, muss die Abtast-Frequenz mindestens doppelt so gross sein wie die maximale Frequenz des Audio-Signals:
F_\text{abtast} > 2 \cdot F_\text{max}Wird dieses Theorem nicht eingehalten, so kann es bspw. zu einer sog. "Spiegelung" kommen.
In diesem Fall führt, wie in der Abbildung zu sehen, das originale Signal (gelb hinterlegt) zu einem falschen Ausgabesignal (blau hinterlegt):
Quantisierung
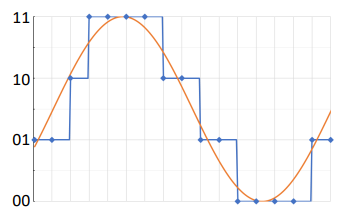
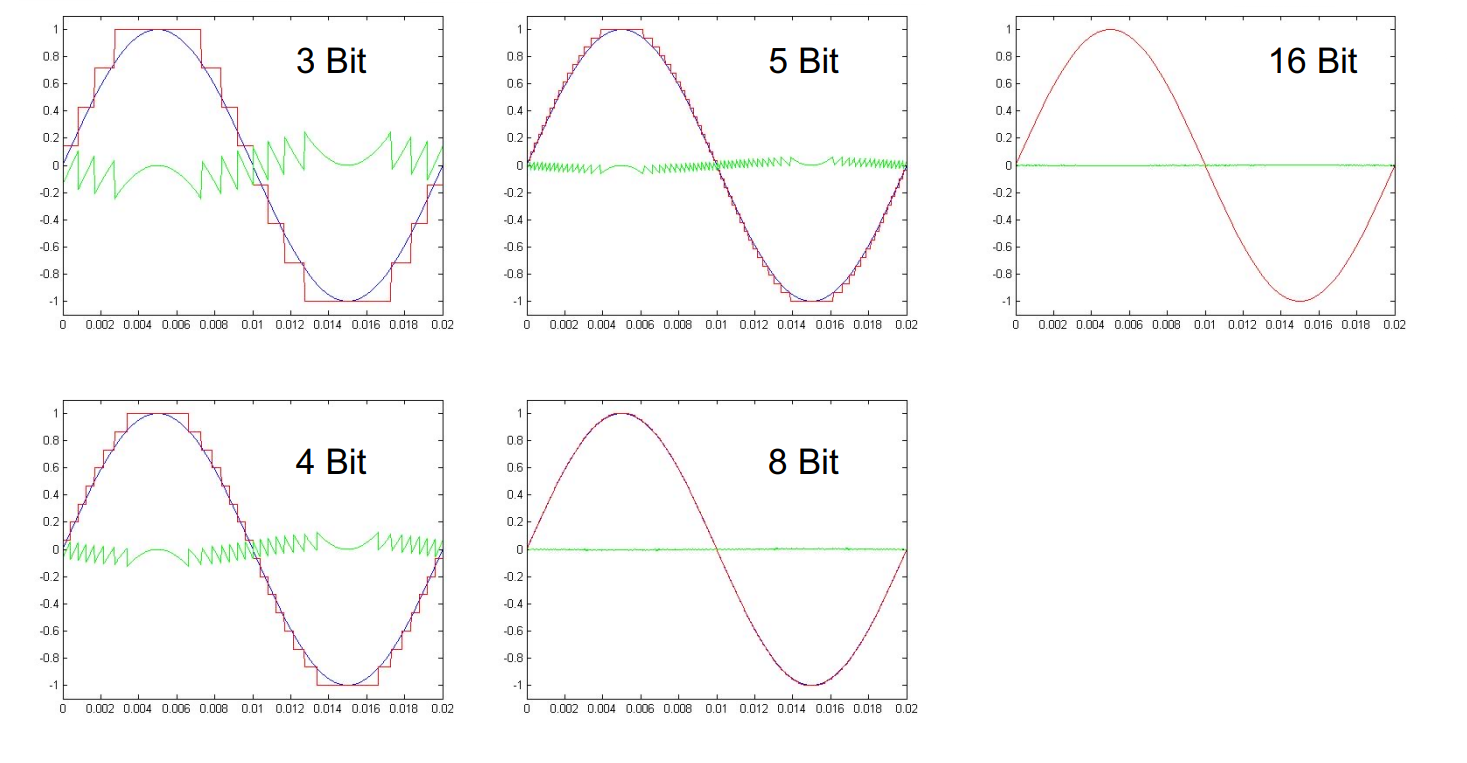
Im Rahmen der Quantisierung wird versucht, mit Hilfe von Quantisierung das Signal so genau wie möglich in binärer Form abzubilden:
Da das quantisierte Signal nicht zu 100% dem originalen Signal entspricht entsteht jeweils ein Rauschen, welches pro zusätzlichem Bit, welches für das Quantisieren verwendet wird, um 6db abnimmt:
Im Vergleich: In der Telefonie wird eine Quantisierung mit 8 Bit vorgenommen - auf Audio-CDs mit 16 Bit. Aus diesem Grund klingen Anrufe sehr "verrauscht".
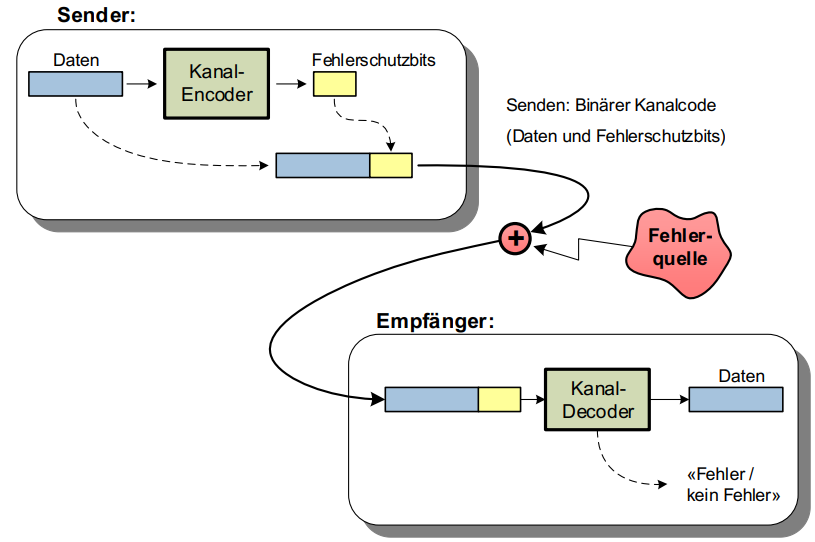
Kanalcodierung
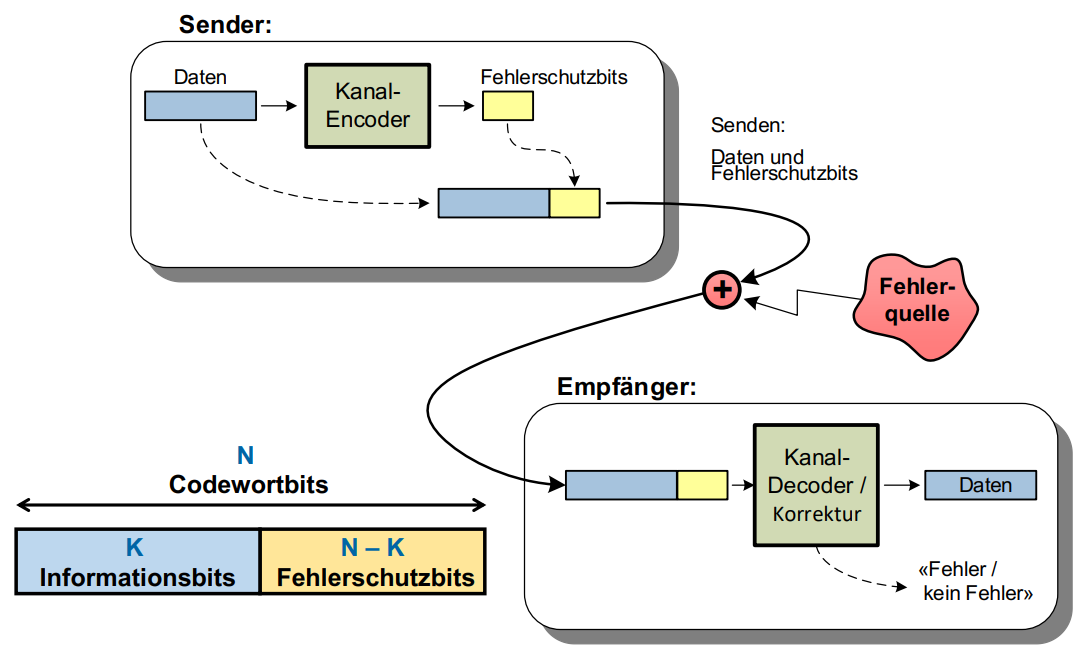
Das Ziel der Kanalcodierung ist das Erkennen und/oder Beheben von Fehlern.
Fehlerkorrekturverfahren
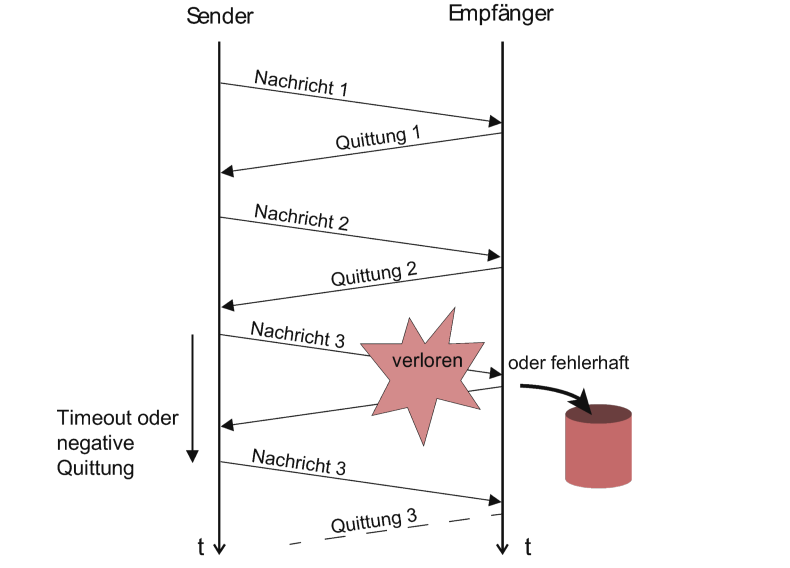
Backward Error Correction
Unter dem Prinzip der Backward Error Correction (Rückwärtsfehlerkorrektur) versteht man, dass Fehler in Daten lediglich erkannt werden, um diese dann erneut beim Sender anzufordern.
Mögliche Hilfsmittel hierfür sind bspw.:
- Blockcodes
- CRC (Cyclic redundancy check (siehe CRC))
Forward Error Correction
Das Prinzip der Forward Error Correction (Vorwärtsfehlerkorrektur) ist es, Fehler nicht nur zu erkennen sondern direkt beim Empfang zu korrigieren.
Mögliche Hilfsmittel sind:
- Blockcodes
- Minimum-Distance-Decoding
- Faltungscodes
Verfahren, die bei jedem Versand eines Pakets auf eine Antwort, dass der Versand erfolgreich war, warten, kosten viel Performance:
Aus diesem Grund ist bspw. das Protokoll TCP, welches eine Flusskontrolle hat, um einiges langsamer als UDP, welches keine Flusskontrolle hat.
Binäre Kanäle
Binäre Kanäle können nur die Werte 0 und 1 übertragen.
Alle Beispiele unterliegen der Annahme, dass ein symmetrischer, binärer Kanal vorliegt (siehe Binary Symmetric Channel).
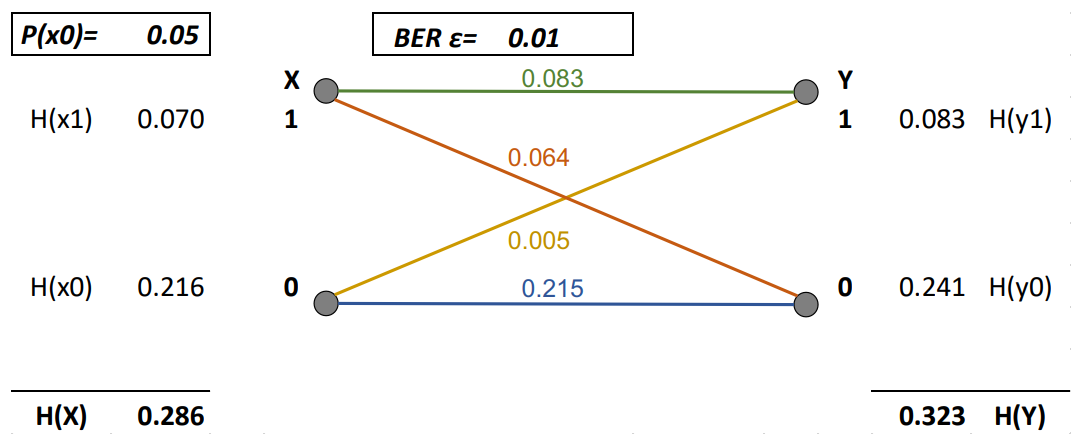
Bitfehlerwahrscheinlichkeit
Die eingezeichnete Störquelle sorgt dafür, dass zu einer Wahrscheinlichkeit \varepsilon eine 0 statt einer 1 oder eine 1 statt einer 0 gesendet wird.
Die Bit Error Ratio BER (Formelbuchstabe \varepsilon) beschreibt, wie hoch die Wahrscheinlichkeit ist, dass ein Fehler auftritt.
Einige Beispiele von Fehlerwahrscheinlichkeiten:
- Alle Bits falsch:
\text{BER} = 1 - Alle Bits richtig:
\text{BER} = 0 - 1 von 2 Bits falsch:
\text{BER} = 0.5 - 1 von 1000 Bits falsch:
\text{BER} = 0.001
Ein asymmetrischer Kanal hat unterschiedliche Wahrscheinlichkeiten:
\varepsilon_{0 \rightarrow 1}: Die Wahrscheinlichkeit, dass eine0durch einen Fehler zu einer1wird\varepsilon_{1 \rightarrow 0}: Die Wahrscheinlichkeit, dass eine1durch einen Fehler zu einer0wird
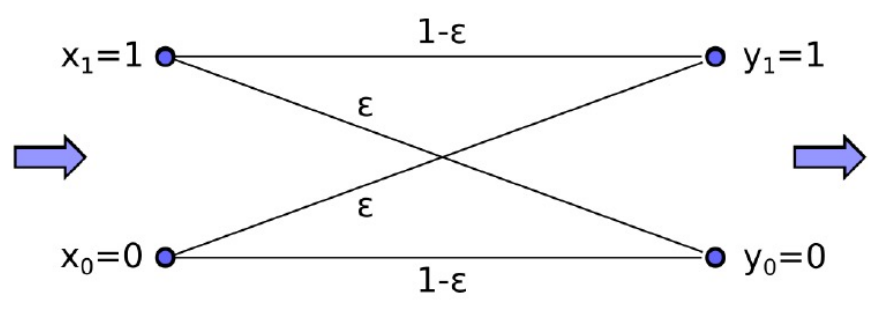
Binary Symmetric Channel
In einem symmetrischen Kanal sind diese beiden Wahrscheinlichkeiten identisch:
\varepsilon_{0 \rightarrow 1} = \varepsilon_{1 \rightarrow 0} = \varepsilonBildlich sieht das folgendermassen aus:
Wahrscheinlichkeit, dass 1 Bit korrekt übertragen wird:
1-\varepsilonWahrscheinlichkeit, dass N Bits korrekt übertragen werden:
(1-\varepsilon)^NMehrbitfehlerwahrscheinlichkeit Berechnen
In einem BSC lässt sich mit Hilfe folgender Formel berechnen, ob in einer Sequenz von N Bits genau F Bitfehler auftreten:
$$P_{F,N} = \underbrace{\begin{pmatrix}
N \
F
\end{pmatrix}}{\text{Anzahl möglicher Anordnungen der Fehler}} \cdot \overbrace{\varepsilon^F}^{\text{Wahrscheinlichkeit für F Fehler}} \cdot \underbrace{(1-\varepsilon)^{N - F}}{\text{Wahrscheinlichkeit, dass alle weiteren Bits korrekt sind}}
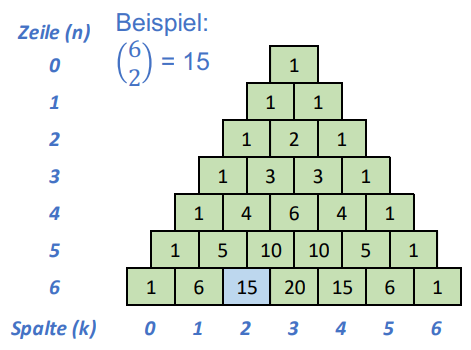
$\begin{pmatrix} N \ F \end{pmatrix}$ berechnet sich hierbei folgendermassen:
$$\begin{pmatrix}
N \
F
\end{pmatrix} = \frac{N!}{F! \cdot (N - F)!}
Alternativ kann das Ergebnis von $\begin{pmatrix} N \ F \end{pmatrix}$ auch aus dem Pascalschen Dreieck abgelesen werden:
Wahrscheinlichkeiten in einem BSC
Folgende Grafik zeigt zudem auf, wie die Wahrscheinlichkeiten in einem BSC aussehen:
Mit Hilfe der im Kapitel Entropie erwähnten Formel lassen sich zudem auch die Entropien der einzelnen Fälle berechnen:
Zwar erhöht der Bitfehler, wie zu sehen, die Entropie, zerstört aber gleichzeitig auch Informationen vom Eingang.
Um also den resultierenden, tatsächlichen unversehrten Informationsgehalt zu errechnen, muss von der resultierenden Entropie H(Y) die Entropie des Bitfehlers H(\varepsilon) abgezogen werden.
I_{BSC} = H(Y) - H(\varepsilon)Die gesamthafte Entropie der Störquelle H(\varepsilon) berechnet sich mit dieser Formel:
H(\varepsilon) = \varepsilon \cdot \log_2\left(\frac{1}{\varepsilon}\right) + (1 - \varepsilon) \cdot \log_2\left(\frac{1}{1 - \varepsilon}\right)Daraus ergibt sich diese Rechnung zum Bestimmen der Kapazität des BSCs aus der Abbildung:
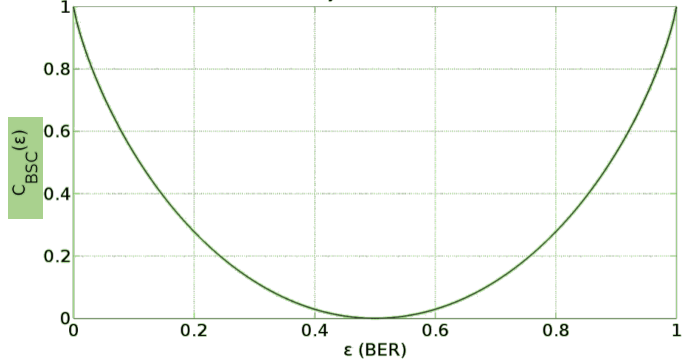
I_{BSC} = H(Y) - H(\varepsilon) = 0.323 - \left(0.01 \cdot \log_2\left(\frac{1}{0.01}\right) + (1 - 0.01) \cdot \left(\frac{1}{1 - 0.01}\right)\right) = 0.323 - 0.081 = 0.242 Bit/BitFolgender Graph zeigt das Verhältnis zwischen der Bitfehler-Rate und der Kanalkapazität auf:
Binäre Kanalcodes
Binäre Kanalcodes sind eine Sammlung Codewörter, welche zusätzlich zu den Daten auch Informationen zwecks Fehlerschutz beinhalten können:
Code-Rate
Die Code-Rate R gibt an, zu wieviel Prozent Code-Wörter aus verwertbaren Informationen bestehen.
Sie errechnet sich aus der gesamtlänge der Code-Wörter N und der Anzahl Informations-Bits K:
R = \frac{K}{N}Hamming-Distanz
Die minimale Hamming-Distanz d_\text{min} gibt wider, wieviele Bits mindestens wechseln müssen, um aus einem Codewort ein anderes zu bilden.
Die Anzahl erkennbarer Fehler ist d_\text{min}-1
Die Anzahl korrigierbarer Fehler \frac{d_\text{min}-1}{2}
Beispiele
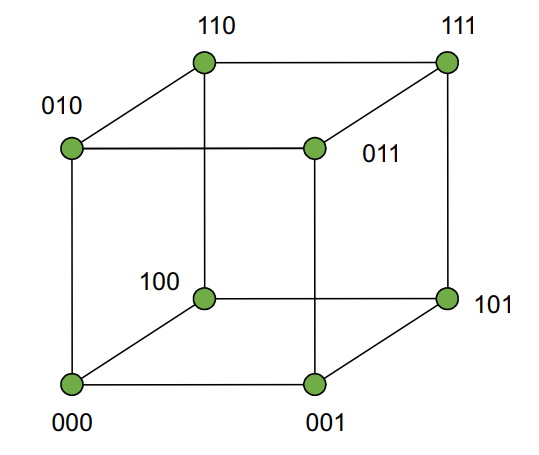
Folgend einige Beispiele anhand einer 3-Bit Codes.
Hamming Distanz 1
Ein Fehler führt zu einer Verwechslung mit einem anderen Codewort:
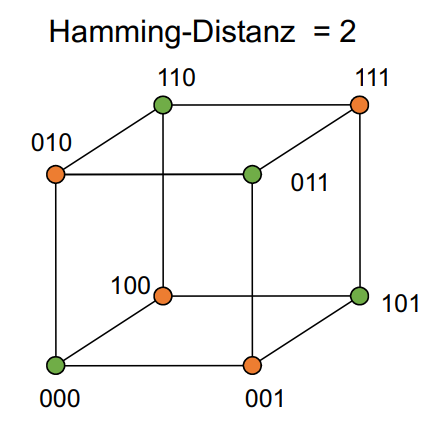
Hamming Distanz 2
Maximal 1 Bitfehler (orange hinterlegt) kann erkannt werden:
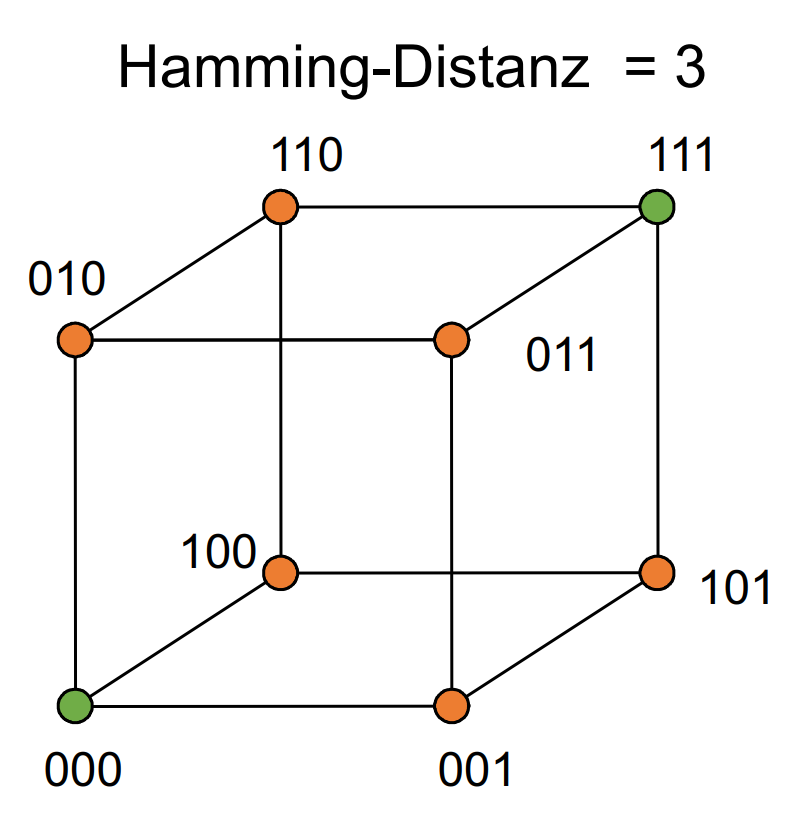
Hamming Distanz 3
Maximal 2 Bitfehler erkennbar, maximal 1 Bitfehler korrigierbar:
Hamming-Gewicht
Das Hamming-Gewicht w_H(x) bezeichnet die Anzahl in einem Code-Wort.
Beispiele:
w_H(000) = 0w_H(001) = w_H(010) = w_H(100) = 1w_H(110) = w_H(101) = w_H(011) = 2w_H(111) = 3
Mit Hilfe des Hamming-Gewitchs lässt sich die Hamming-Distanz mathemtaisch berechnen:
d(x, y) = w_H(x \oplus y)Eigenschaften von Binären Kanalcodes
Perfekt
Alle möglichen Sequenzen haben eine minimale Hamming-Distanz zu einem korrekten Code-Wort zu dem es somit zugewiesen werden kann.
Systematisch
Die Informations-Bits (die zu versendenden Daten) sind an einem Stück
Beispiele:
oder
Linear
Zwei beliebige gültige Code-Wörter geben, rechnet man sie mit XOR \oplus zusammen, wiederum ein gültiges Code-Wort.
Hinweis:
Durch Generator-Matrizen erstellte Codes sind immer linear (siehe Lineare Block-Codes).Ob ein Block-Code linear ist kann nur mit Sicherheit überprüft werden, indem man alle Code-Wörter untereinander mit
XOR\opluszusammenrechnet und prüft, ob das Ergebnis ein gültiges Code-Wort ist.
Zyklisch
Die zyklische Verschiebung eines gültigen Code-Wortes ergibt ein gültiges Codewort:
Beispiele dazu:
Fehlererkennung
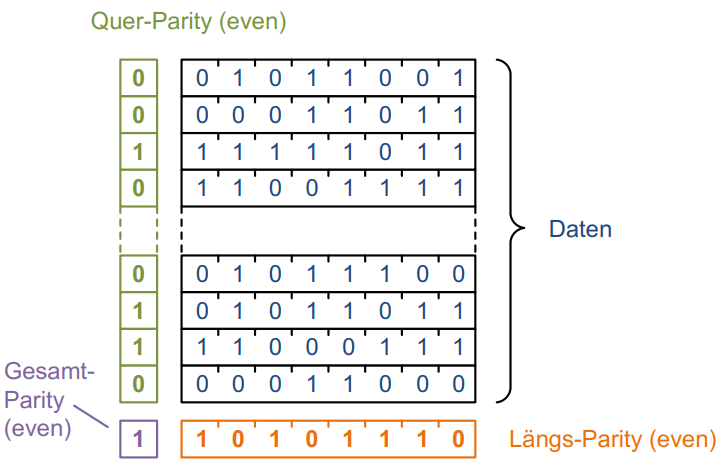
Paritäts-Check
Der einfachste Weg, Daten auf deren Gültigkeit zu prüfen. Für den Paritäts-Check werden alle Bits eines Datenstroms mit XOR \oplus zusammengerechnet. Das Ergebnis ist die sogenannte Parität. Ist diese beim Empfang der Daten ungültig, so ist beim Versand ein Fehler aufgetreten.
Beispiel eines Paritäts-Checks:
Cyclic Redundancy Check CRC
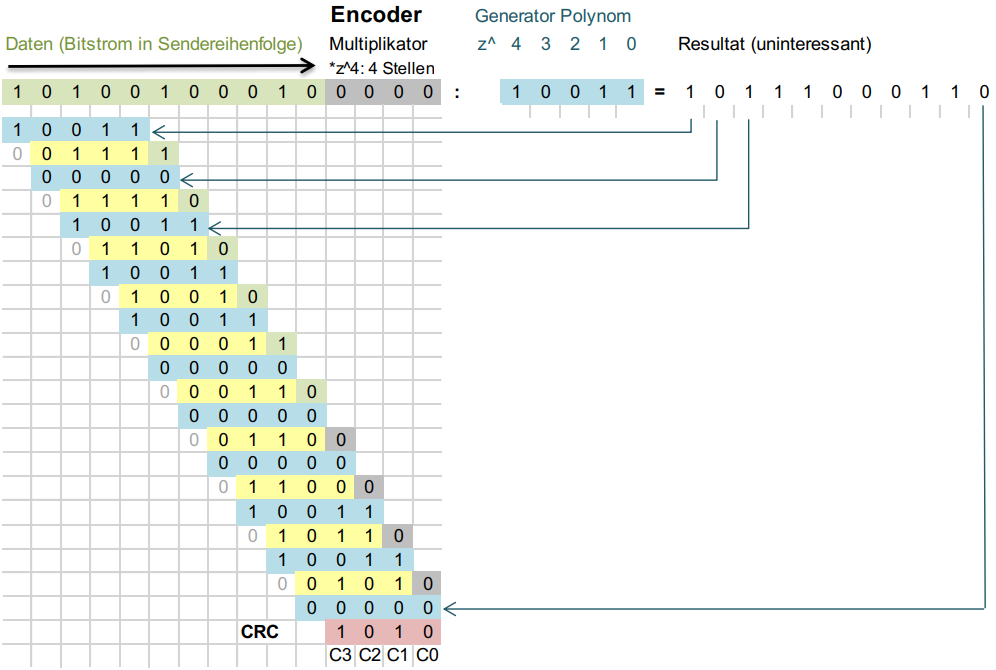
Der Cyclic Redundancy Check (oder CRC) ist ein Algorithmus zum einfachen Prüfen eines Datenstroms auf Fehler.
Um eine CRC Prüfsumme zu erstellen und zu prüfen, muss man sich vorgängig auf ein Generator Polynom einigen (das heutzutage gängigste ist bspw. crc32).
Um den CRC zu berechnen, muss dem Datenstrom die Anzahl Stellen des Generator-Polynoms minus 1 angefügt werden (grau hinterlegt). Die daraus errechnete Zahl muss anschliessend durch das Generator-Polynom (blau hinterlegt) dividiert werden.
Der daraus entstehende Rest (rot hinterlegt) ist die CRC Prüfsumme.
Anschliessend wird der Datenstrom zusammen mit dem CRC (an Stelle des grau hinterlegten Platzhalters) versendet.
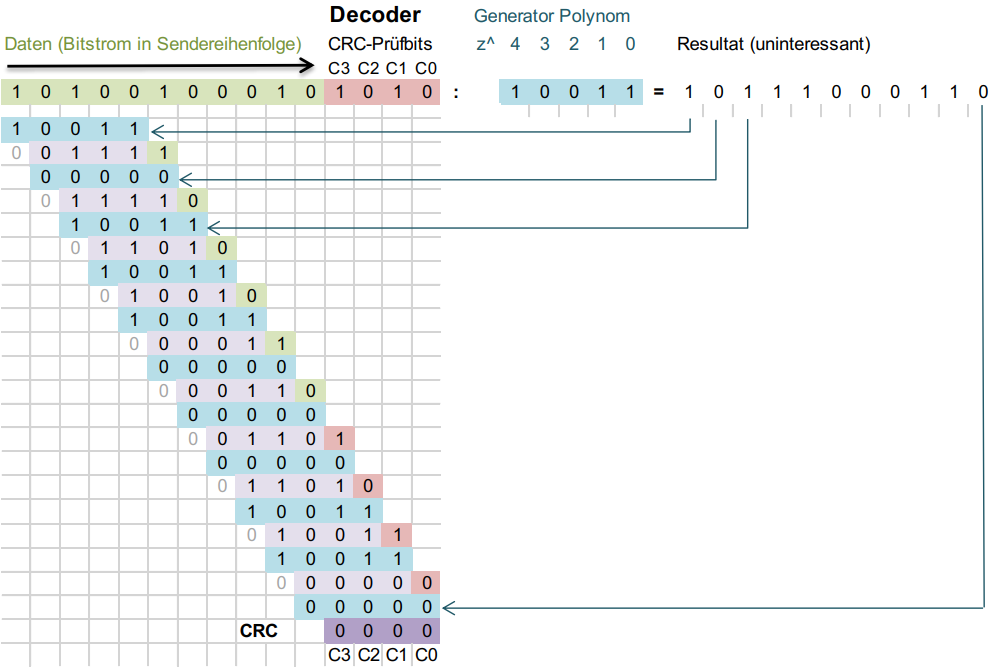
Geprüft wird die Gültigkeit indem der ankommende Datenstrom durch das Generator-Polynom geteilt wird. Ist der Rest 0, so sind die Daten korrekt:
Fehlerkorrektur
Ander als in der Fehlererkennung sollen in der Fehlererkennung einige Fehler auch ohne weiteres beim Empfänger korrigiert werden können.
Das Konzept sieht hierbei folgend aus:
Die Formel zum Errechnen von der Anzahl Prüfbits P für die Übertragung von K Informations-Bits:
p \approx I(K + 1)
Für 200 Informations-Bits:
p \approx \log_2(200 + 1) = 7.6\text{ bit} \approx 8\text{ bit}
Lineare Block-Codes
Hamming Codes gehören zu den linearen Block-Codes.
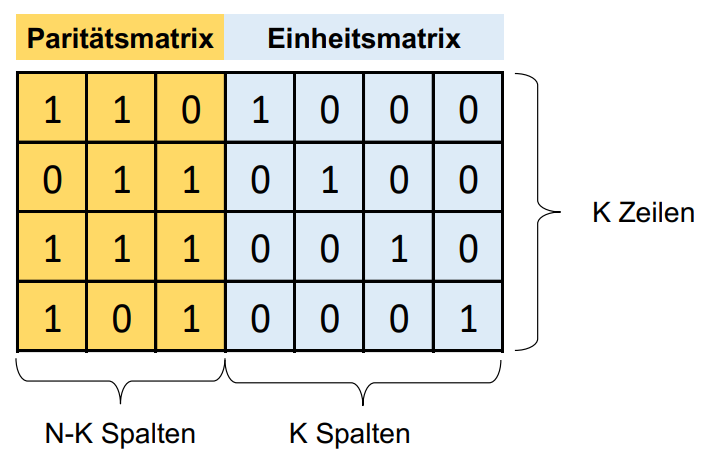
Lineare Block-Codes werden mit Hilfe einer Generatormatrix gebildet, welche aus einer Paritäts-Matrix und einer Einheits-Matfix besteht:
Die Paritätsmatrix wird verwendet, um die Prüfsumme zu erstellen, die Einheitsmatrix, um die eigentliche Information einzufügen.
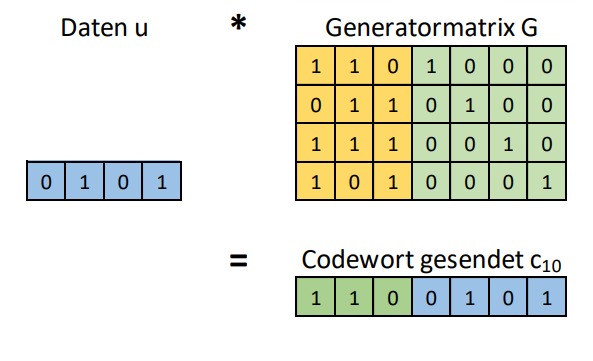
Berechnet werden die generierten Bits ähnlich wie in einer Matrix Rechnung.
Will man bspw. die Daten 0101 versenden, ist die Rechnung für das 1. Bit folgendermassen:
Die erste Spalte für das 1. Bit befindet sich in der Paritätsmatrix und lautet 1011.
Die Rechnung ist (0 \wedge 1) \oplus (1 \wedge 0) \oplus (0 \wedge 1) \oplus (1 \wedge 1) = 1
Folgend sieht die Lösung für das Berechnen aller Bits aus:
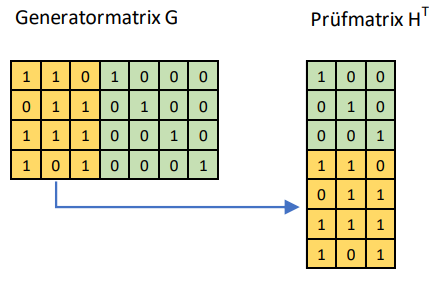
Die Prüfmatrix kann gebildet werden, indem die horizontale Einheitsmatrix entfernt und durch eine vertikale Einheitsmatrix ersetzt wird:
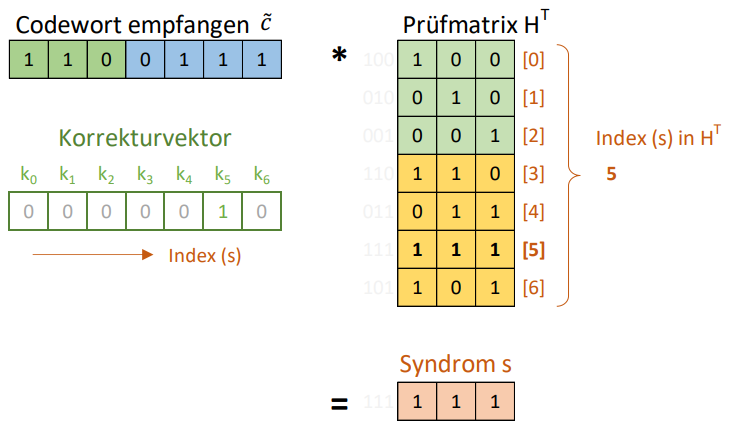
Berechnet man auf dieselbe Weise wie zuvor das Produkt eines Code-Wortes mit der Prüf-Matrix erhält man als Ergebnis 0, falls die Übertragung korrekt war.
Ansonsten erhält man das sogenannte "Syndrom" des Indexes des Bits, welches falsch übertragen wurde:
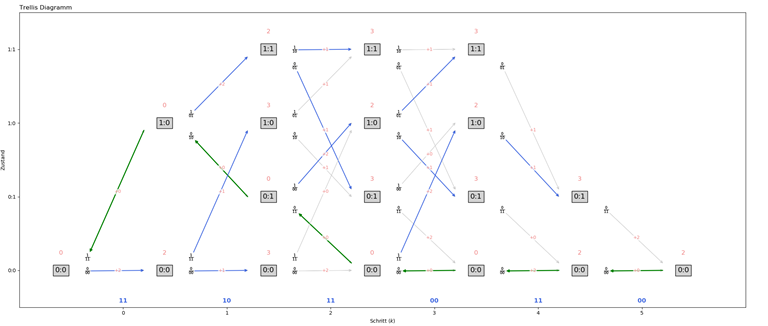
Faltungscode
Folgendes Bild zeigt auf, wie mit Hilfe eines Trellis-Diagramms ein Faltungscode errechnet und auch wieder decodiert wird:
Die freie Hamming-Distanz kann am einfachsten vom Zustandsdiagramm abgelesen werden.
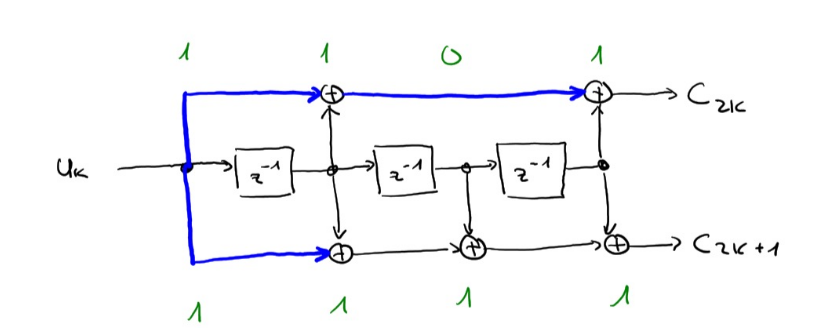
Schaltungs-Umsetzung eines Faltungscodes
Glossar
| Wort | Definition |
|---|---|
| Zahlensystem | System zum Darstellen von Zahlen (bspw. Dezimalsystem, Hexadezimal-System siehe Zahlensysteme) |
| Bit (Binary Digit) | Speicher für 1 Bit (true/false) |
| Byte (Octet) | 8 Bit oder 2 Nibble à 4 Bit  |
| Word | Wert mit (meist) 16 Bit:  |
Doubleword (DWord) |
Aneinanderreihung von 2 Worten:  |
Quadword (QWord) |
Aneinanderreihung von 4 Worten |
| Octaword | Aneinanderreihung von 8 Worten |
| DMS | Eine DMS - Discrete Memoryless Source - liefert voneinander unabhängige, zufällige Werte |
| BMS | Eine BMS - Binary Memoryless Source - liefert voneinander unabhängige, zufällige binäre Werte ($0$en und $1$en) |
Probability P(x) |
Die Wahrscheinlichkeit, dass das Symbol x in einer Nachricht auftritt (siehe Probability) |
Informationsgehalt I(x) |
Der Informationsgehalt, der ein übermitteltes Symbol hat (siehe Informationsgehalt) |
Entropie H(x) |
Der durchschnittliche Informationsgehalt einer Quelle (siehe Entropie) |
Mittlere Codewortlänge L(x) |
Die durchschnittliche Länge, welche die Codeworte einer Codierung haben (siehe Codewortlänge) |
Redundanz R(x) |
Die Redundanz beschreibt, wieviele unnötige Daten Codeworte einer Codierung enthalten. Eine niedrige Redundanz ist besser. (siehe Redundanz) |
RLE (Run Length Encoding) |
Codierung in der ein sich oft wiederholendes Symbol komprimiert darstellen lässt (siehe RLE) |
Luminanz Y |
Graustufen-Intensität (siehe JPEG) |
| Spiegelung | Eine der möglichen Fehlern, die beim Digitalisieren eines Audiosignals auftreten kann (siehe Abtasttheorem) |
| Backward Error Correction | Das Erkennen von Fehlern in empfangenen Daten |
Bit Error Ratio BER |
Die Bit Error Ratio beschreibt, wie hoch die Wahrscheinlichkeit ist, dass Bit-Fehler in einem Binären Kanal auftreten. (siehe Bitfehlerwahrscheinlichkeit) |
| Hamming-Distanz | Die minimale Anzahl unterschiedlicher Bits zwischen 2 Code-Worten in einem Blockcode (siehe Hamming-Distanz) |
| Hamming-Gewicht | Die Anzahl $1$en in einem Code-Wort (siehe Hamming-Gewicht) |
Code-Rate R |
Die Code-Rate beschreibt, das Verhältnis der Anzahl Informationsbits gegenüber der gesamtlänge der Codewörter (siehe Code-Rate) |
| Syndrom | Ein Wert, der darauf hinweist, dass an einer gewissen Bit-Stelle ein Fehler geschehen ist. |