16 KiB
Inhaltsverzeichnis
- Inhaltsverzeichnis
- Aussagenlogisches Rechnen
- Beweistechniken
- Mengen
- Relationen
- Themen
- Glossar
Aussagenlogisches Rechnen
Operatoren
\neg A
Gesprochen: "Nicht $A$"A \wedge B
Gesprochen: "Aund $B$"A \vee B
Gesprochen: "Aoder $B$"A \Rightarrow B
Entspricht\neg A \vee B. Gesprochen: "Aimpliziert $B$"A \Leftrightarrow B
Gesprochen: "Aäquivalent $B$"
Regeln
Regeln der Doppelten Negation
\neg\neg A \Leftrightarrow AAbsorption
A \wedge A \Leftrightarrow AA \vee A \Leftrightarrow AKommutativität
Operanden können beliebig vertauscht werden:
A \wedge B \Leftrightarrow B \wedge AA \vee B \Leftrightarrow B \vee AAssoziativität
Identische Operationen können in beliebiger Reihenfolge ausgeführt werden:
(A \wedge B) \wedge C \Leftrightarrow A \wedge (B \wedge C)(A \vee B) \vee C \Leftrightarrow A \vee (B \vee C)Distributivität
Unterschiedliche Operationen können "ausmultipliziert" werden:
A \wedge (B \vee C) \Leftrightarrow (A \wedge B) \vee (A \wedge C)A \vee (B \wedge C) \Leftrightarrow (A \vee B) \wedge (A \vee C)Regeln von De Morgan
\neg(A \wedge B) \Leftrightarrow \neg A \vee \neg B\neg(A \vee B) \Leftrightarrow \neg A \wedge \neg BQuantoren
\forall x\, A(x)
Gesprochen: "Für allexgilt $A(x)$"\forall x \in M A(x)
Gesprochen: "Für allexaus der MengeMgiltA(x)\exists x\, A(x)
Gesprochen: "Es gibt einxmit $A(x)$"\exists x \in M A(x)
Gesprochen: "Es gibt einxaus der MengeMmit $A(x)$"
\forall x \forall y\, A(x,y) \Leftrightarrow \forall{x,y}\, A(x,y) und \exist x \exist y\, A(x,y) \Leftrightarrow \exist{x,y}\, A(x,y)
Hinweis:
Die Bezeichnung fär die Symbole\forallund\existsind Allquantor und Existenzquantor.
Regeln
- Vertauschungsregel für unbeschränkte Quantoren
\forall x\, A(x) \Leftrightarrow \neg\exist x\, \neg A(x) - Vertauschungsregel für beschränkte Quantoren
\forall x \in K\, A(x) \Leftrightarrow \neg\exist x \in K \neg A(x) - Beschränkter und unbeschränkter Allquantor
\forall x \in K A(x) \Leftrightarrow \forall x(x \in K \Rightarrow A(x)) - Beschränkter und unbeschränkter Existenzquantor
\exist x K A(x) \Leftrightarrow \exist x(x \in K \wedge A(x))
Beweistechniken
Beweis durch Implikation
Anwendbar bei Formeln in der Form:
A \Rightarrow B- Zwingende Voraussetzungen für die Bedingung
Aerfassen - Prüfen, ob
Brichtig ist
Beispiel:
A: "xundysind gerade."
B: "x \cdot yist gerade."Damit
xundygerade sind, müssen sie ein Produkt von2sein. Die Behauptung ist also:
x = 2 \cdot n_xundy = 2 \cdot n_y
n_xundn_ysind hierbei beliebige natürliche Zahlen.Für den Nachweis ergibt sich folgendes für
B:x \cdot y = (2 \cdot n_x) \cdot (2 \cdot n_y) = 22 \cdot (n_x \cdot 2 \cdot n_y)Da das Ergebnis ein vielfaches von
2ist, heisst das, dassx \cdot ygerade ist und somit die AussageA \Rightarrow Bwahr ist.
Beweis durch Widerspruch
Anwendbar bei einfachen Aussagen.
Der Merksatz ist hierbei: "Wenn die Aussage nicht nicht wahr ist, ist sie wahr."
Der Vorgang ist hierbei, die ursprüngliche Aussage zu negieren und zu beweisen, dass die negierte Aussage unerfüllbar ist.
Beispiel:
A: "Es gibt keine grösste natürliche Zahl."
\neg A: "Es gibt eine grösste natürliche Zahl."
msei dei grösste natürliche Zahl. Für jede natürliche Zahlxgibt es ein Inkrement, welches man mit Hilfe vonx + 1errechnen kann. So gibt es auch fürmein Inkrementm + 1, welches um1grösser ist alsm. Somit sit die negierte Aussage\neg Aunerfüllbar.Aist wahr.
Beweis durch (Gegen-)Beispiel
Anwendbar bei Aussagen mit Quantoren (\forall "für alle" und \exists "existiert").
Die Strategie hierbei ist, ein anwendbares Beispiel (im Falle \exists) oder Gegenbeispiel (im Falle \forall) zu finden.
Beispiel:
A: "Es existieren Zahlen, welche kein Quadrat einer natürlichen Zahl sind."Dies lässt sich an dem Beispiel
2beweisen.2ist weder ein Quadrat von1(1^2 = 1) noch von2(2^2 = 4).
Beweis durch Kontraposition
Anwendbar bei Aussagen in der Form A \Rightarrow B
Es gilt für diese Strategie, die dazugehörige Kontraposition \neg B \Rightarrow \neg A zu belegen.
Beispiel:
A: "Für jede natürliche Zahlngilt:(n^2 + 1 = 1) \Rightarrow (n = 0)Die Kontraposition dazu lautet wie folgt:
A': "Für alle Zahlen, die nicht0sind giltn^2 + 1 \not= 1Da alle Zahlen
> 0ein Quadrat haben, das grösser als0ist, gilt:n^2 + 1 > 1. Daraus folgt, dass AussageAwahr ist.
Beweis durch Äquivalenz
Anwendbar für Aussagen der Form A \Leftrightarrow B
Die Strategie ist hierbei, zu beweisen, dass A \Rightarrow B gilt und B \Rightarrow A gilt.
Beispiel:
A: (n^2 + 1 = 1) \Leftrightarrow (n = 0)Wenn
n = 0ist, ergibt sich aus(n^2 + 1 = 1)folgendes:(0^2 + 1 = 1) = (0 + 1 = 1). Damit istA \Rightarrow Bbewiesen.Die einzige Situation in der
(n^2 + 1 = 1)oder eher(n^2 = 0)ergibt, ist, wennn0entspricht. Damit ist auchB \Rightarrow Abewiesen.
Wahrheitstabelle
Folgend ein Beispiel einer Wahrheitstabelle:
a |
b |
c |
b \vee c |
a \Rightarrow (b \vee c) |
|---|---|---|---|---|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Normalformen
Normalformen beinhalten generell nur ANDs (\wedge), ORs (\vee) und NOTs (\neg)
Negationsnormalform NNF
Die Negationsnormalform (NNF) ist die Form einer Formel, in der nur atomare (nicht aufteilbare) Teilformeln negiert sind.
Beispiel:
(A \wedge (\neg B \vee (C \vee D)))Merke, dass nur
B, welches atomar ist, negiert ist.
Disjunktive Normalform DNF
Die Disjunktive Normalform ist eine Umformung der Formel, in der alle Belegungen für die die Formel true ergibt, mit einander "verodert" werden.
Beispiel:
DieDNFfür die Formel\neg A \wedge (B \vee C)lautet folgendermassen:(\neg A \wedge \neg B \wedge C) \vee (\neg A \wedge B \wedge \neg C) \vee (\neg A \wedge B \wedge C)Herleitung:
Schritt 1: Wahrheitstabelle aufstellen:
ABCB \vee C\neg A \wedge (B \vee C)0000000111010110111110000101101101011110Schritt 2: $1$-Stellen aufschreiben:
\neg A \wedge \neg B \wedge C\neg A \wedge B \wedge \neg C\neg A \wedge B \wedge CSchritt 3: Formeln für $1$-Stellen "verodern":
(\neg A \wedge \neg B \wedge C) \vee (\neg A \wedge B \wedge \neg C) \vee (\neg A \wedge B \wedge C)
Konjunktive Normalform KNF
Bei der Konjunktiven Normalform wiederum, werden alle negierten Belegungen, in denen die gegebene Formel false ergibt miteinander "geandet".
Beispiel:
DerKNFvonB \vee (A \wedge C)ist:(A \vee B \vee C) \wedge (A \vee B \vee \neg C) \wedge (\neg A \vee B \vee C)Herleitung:
Schritt 1: Wahrheitstabelle aufstellen:
ABCA \vee CB \vee (A \wedge C)0000000100010010110110000101111100111111Schritt 2: $0$-Stellen aufschreiben und negieren:
\neg A \wedge \neg B \wedge \neg C
Negation:A \vee B \vee C\neg A \wedge \neg B \wedge C
Negation:A \vee B \vee \neg CA \wedge \neg B \wedge \neg C
Negation:\neg A \vee B \vee CSchritt 3: Negierte Ausdrücke mit
ANDs verketten:(A \vee B \vee C) \wedge (A \vee B \vee \neg C) \wedge (\neg A \vee B \vee C)
Ableitungsbaum
Der Ableitungsbaum bietet einen übersichtlichen Weg um Gleichungen in der Aussagenlogik zu lösen.
Folgend ein Beispiel:
Es sei (x \Rightarrow y) \wedge z mit folgender Belegung:
B(x) = \topB(y) = \botB(z) = \top
Der dazugehörige Ableitungsbaum ist dann:
flowchart BT
op3(("∧: 0"))
op2(("∨: 0"))
op1(("¬: 0"))
x["x: 1"]
y["y: 0"]
z["z: 1"]
x --- op1
op1 --- op2
y --- op2
op2 --- op3
z --- op3
Mengen
Mengen haben keine Sortierung und keine doppelten Elemente.
Hinweise:
- Mengen heissen "disjunkt", wenn sie keine gemeinsamen Elemente beinhalten.
Syntax
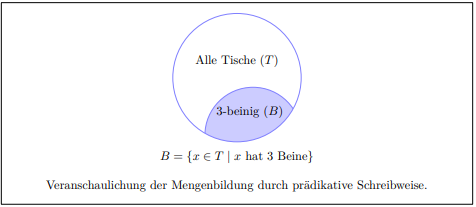
M = \{ x \in \N | x > 5\}
\in
Gesprochen: "Element von"\notin
Gesprochen: "Nicht Element von"|
Gesprochen: "Für die gilt"
"M ist die Menge aller x, für die gilt, dass x > 5 ist."
M = { 5, 6, 7, 8, ... }
Operationen
Subset \subseteq
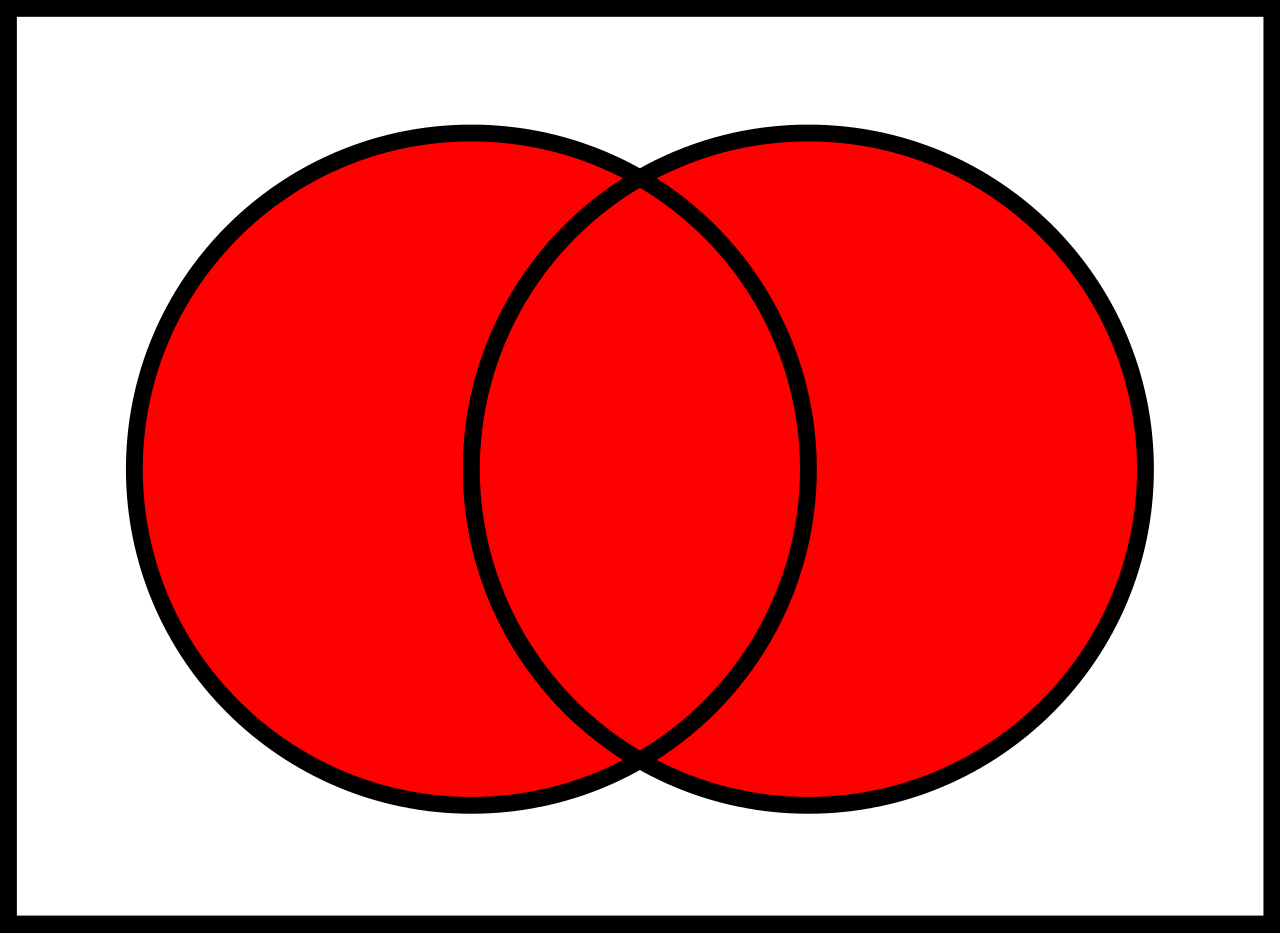
Vereinigung \cup
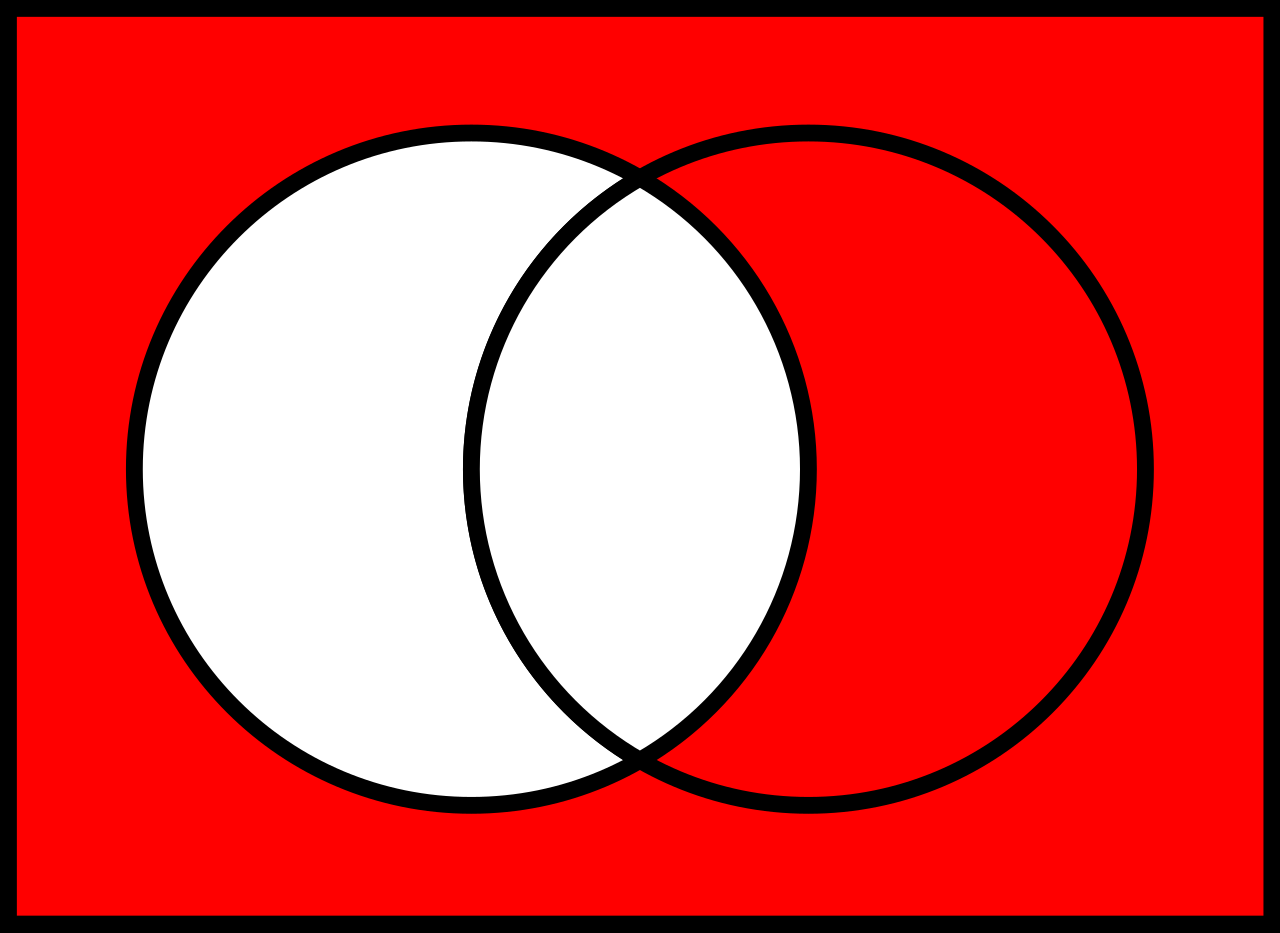
Die Vereinigung "Union" beschreibt die Zusammenfassung zweier Mengen:
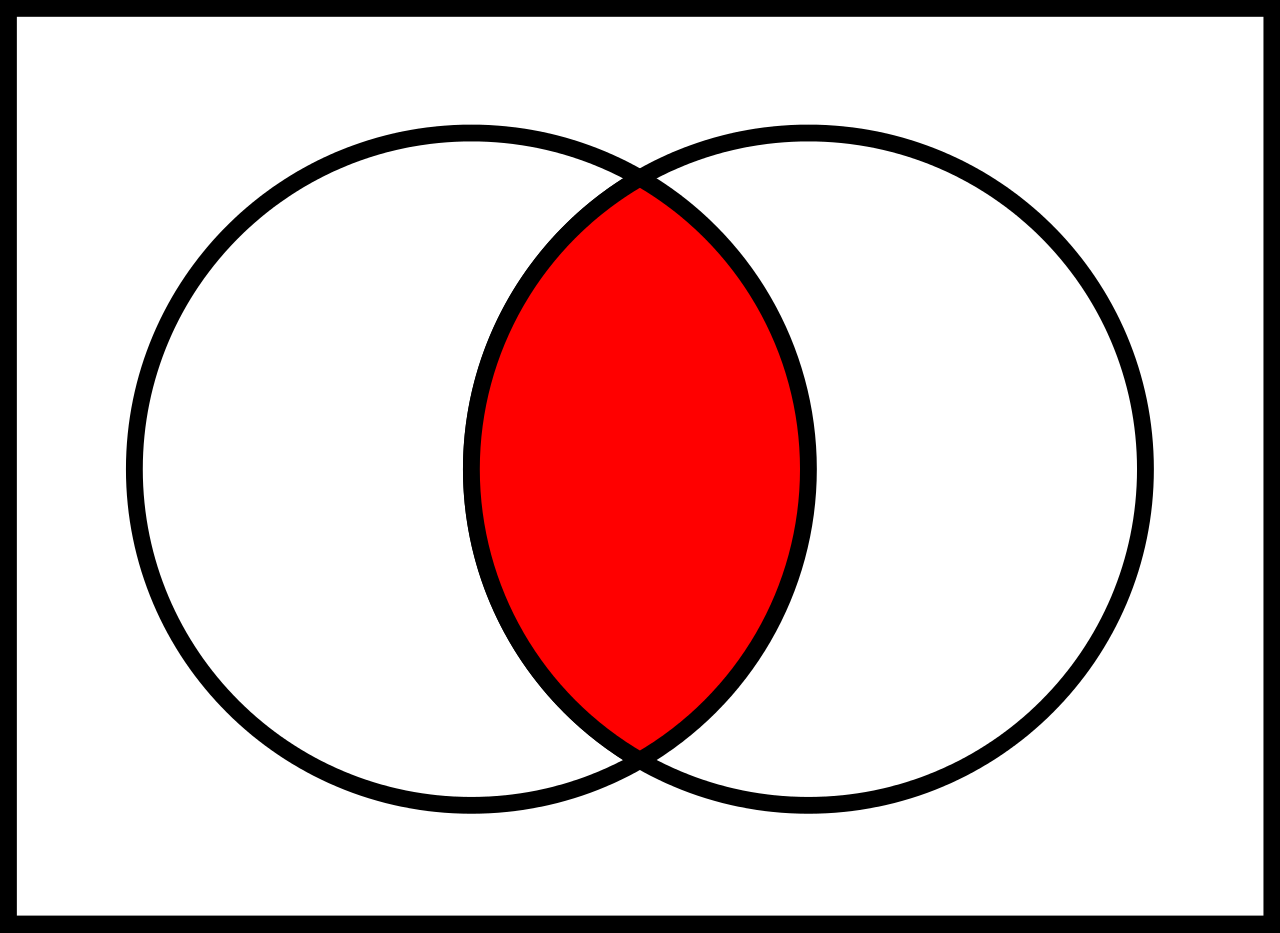
Schnittmenge \cap
Die Schnittmenge "Intersection" zweier Mengen:
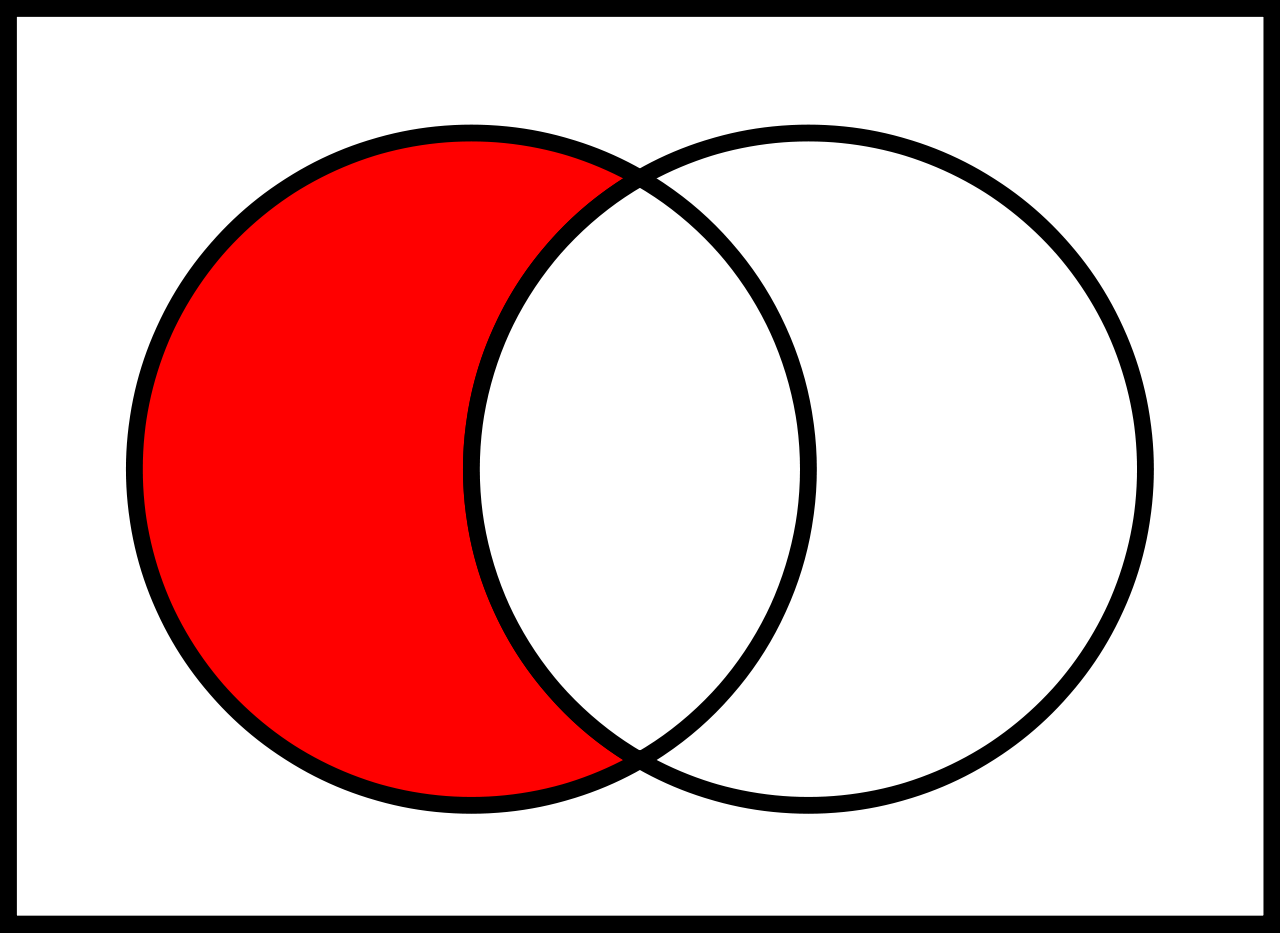
Differenz \setminus
Beschreibt die Differenzmenge zweier Mengen:
A \setminus B gesprochen: "A ohne $B$"
Komplement/Negation \overline{A}
Das Komplement einer Menge A wird wie folgt geschrieben:
\overline{A}Sie beschreibt alle Elemente, die nicht in der Menge A vorkommen:
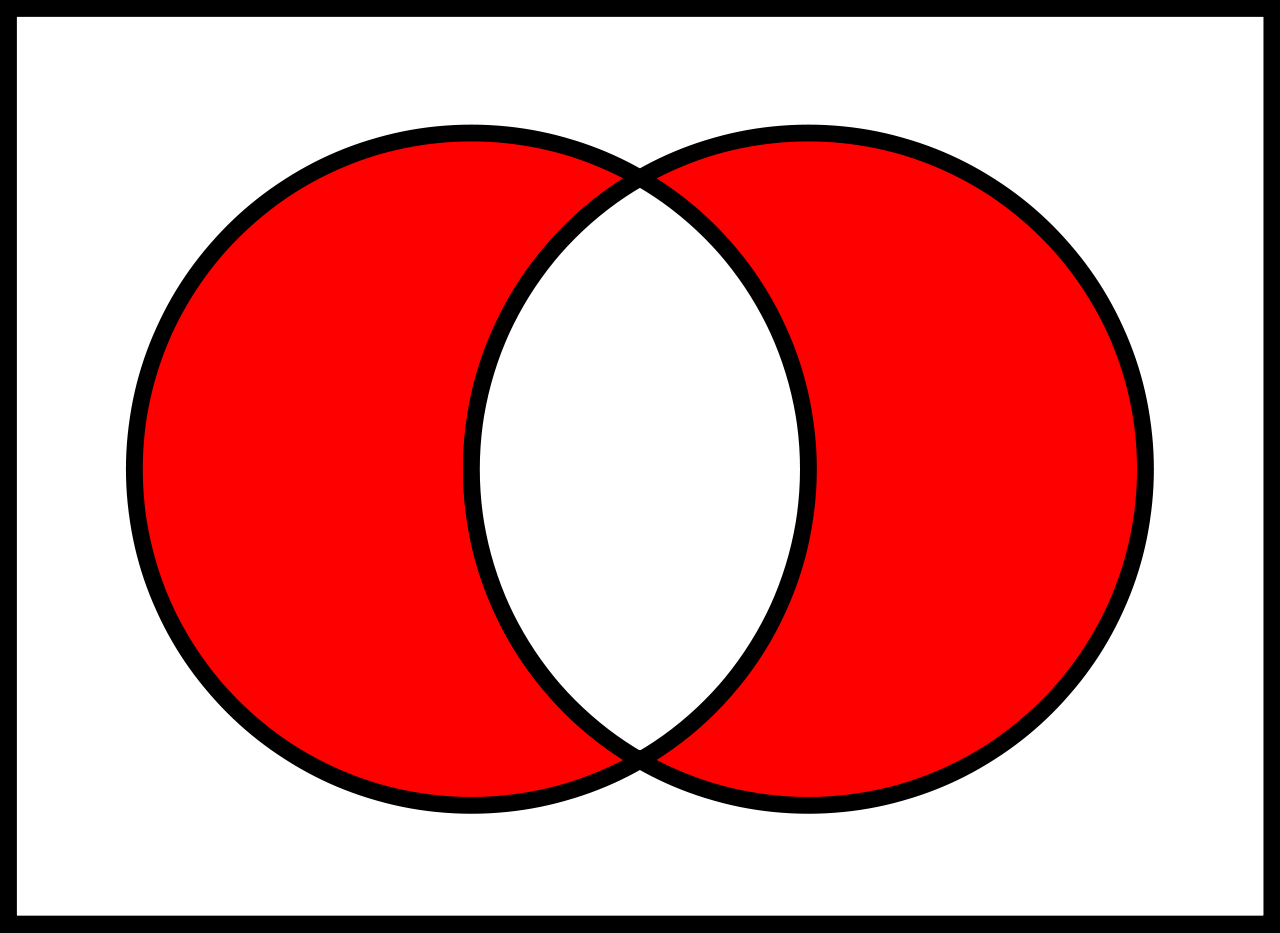
Symmetrische Differenz \triangle
Die Vereinigung zweier Mengen abzüglich deren Schnittmenge:
A \triangle B = (A \setminus B) \cup (B \setminus A) gesprochen "A ohne B vereinigt mit B ohne $A$"
Mächtigkeit \vert A \vert
Die Mächtigkeit \vert A \vert beschreibt, wieviele Elemente eine Menge A beinhaltet.
Beispiel:
\vert \{1, 78, 28\} \vert = 3
Kartesisches Produkt \times
Das Kartesische Produkt ist eine Menge aller Folgen, die aus den Elementen der beiden Mengen gebildet werden können.
Beispiel:
A = \{a, b\}B = \{2, 3, 4\}A \times B = \{a, b\} \times \{2, 3, 4\} = \{(a, 2), (a, 3), (a, 4), (b, 2), (b, 3), (b, 4)\}Die Mächtigkeit von A \times B ist gleich \vert A \vert \cdot \vert B \vert
Hinweis:
Folgen sind sortiert das bedeutet folgendes:A \times B \not = B \times A
Rechenregeln
Kommuntativität
Vordefinierte Mengen
\N: Natürliche Zahlen - Zahlen\geq 0\Z: Alle ganzen Zahlen (positiv und negativ)
Potenzmenge \mathcal{P}
Die Potenzmenge gibt alle möglichen Kombinationen aus einer gegebenen Menge zurück. Die Funktion \mathcal{P}(x) ist folgendermassen definiert:
\mathcal{P}(A) := \{x | x \subseteq A \}Beispiel:
\mathcal{P}(\{0, 1\}) = \{\emptyset, \{0\}, \{1\}, \{0, 1\}\}
Bemerkung:
Die Mächtigkeit einer Potenzmenge errechnet sich folgendermassen:|\mathcal{P}(A)| = 2^{|A|}
Partition
Eine Partition einer Menge A ist eine Menge von Teilmengen von A.
Diese Teilmengen müssen folgende Bedingungen erfüllen:
- Die Mengen dürfen nicht leer sein
- Teilmengen dürfen untereinander keine gemeinsamen Elemente haben
Unendlichkeit
Unendliche Mengen sind unter folgenden Bedingungen abzählbar oder überabzählbar:
- Abzählbar unendlich, wenn sie gleich mächtig wie
\Nsind - Überabzählbar unendlich, wenn sie mächtiger als
\Nsind
Rechnen mit Unendlichkeit
A sei eine abzählbar unendliche und B eine überabzählbar unendliche Menge:
A \cup Bist abzählbar, da im Ergebnis nur Elemente aus der abzählbaren MengeAenthalten sind.A \cap Bist überabzählbar, da alle Elemente der überabzählbaren MengeBim Ergebnis enthalten sindB \setminus Aist überabzählbar, da von der überabzählbaren MengeBnur die abzählbaren Elemente abgezogen werden.
Relationen
DAG ("discrete acyclic graph") ein "gerichteter azyklischer Graph" ist ein Graph, in dem keine Zyklen enthalten sind:
Folgendes ist ein DAG:
flowchart LR
a((A))
b((B))
c((C))
d((D))
e((E))
f((F))
g((G))
a --> b
b --> c
c --> e
b --> e
b --> d
g --> d
d --> e
e --> f
Folgendes ist kein DAG:
flowchart LR
a((A))
b((B))
c((C))
d((D))
e((E))
f((F))
a --> b
b --> c
d --> b
c --> e
e --> f
e --> d
Äquivalenzklasse
Eine Äquivalenzklasse beinhaltet alle Elemente, welche einer Klasse zugeordnet werden können
Äquivalenzrelation
Themen
- Chinesischer Restsatz
- Euklidischer Algorithmus (ggt, kgv berechnen)
Glossar
| Bezeichnung | Beschreibung |
|---|---|
| Knotenmenge | Die Menge aller Elemente (Knoten), die in einem Graphen vorkommen. |
| Wahrheits-Konstanten | \top steht für true, \bot für false. |