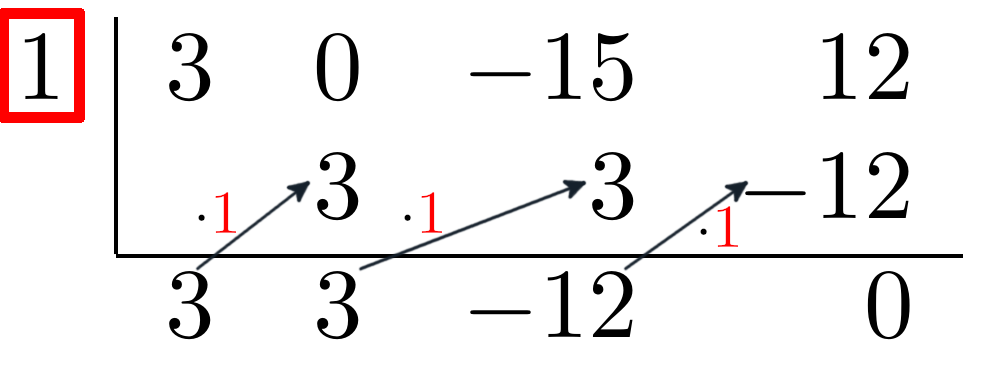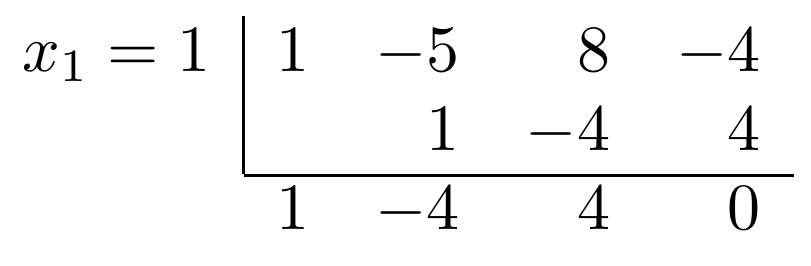26 KiB
Zusammenfassung Analysis 2
Inhalt
- Zusammenfassung Analysis 2
- Inhalt
- Nullstellen durch Horner-Schema
- Stammfunktion
- Integrale
- Uneigentliche Integrale
- Differentialgleichungen
- Anwendung der Integralrechnung
- Taylor-Reihen
Nullstellen durch Horner-Schema
Das Horner-Schema erlaubt es, Nullstellen leicht zu bestimmen.
Der Vorgang wird anhand der folgenden Gleichung aufgezeigt:
f(x) = 3x^3 - 15x + 12Eine Nullstelle dieser Formel ist die 1. Dies lässt sich wie folgt mit dem Horner-Schema prüfen:
1. Nullstelle aufschreiben
Im Bild rot markiert
2. Die Koeffizienten aller $x$-Potenzen aufschreiben
Zu sehen im Bild in der obersten Reihe.
Entspricht eine der Koeffizienten 0 (wie in diesem Beispiel x^2), so muss im Horner-Schema eine 0 eingetragen werden.
4. Startwert notieren
Die Berechnung wird gestartet indem man den ersten Koeffizient (in diesem Fall 3) in die unterste Reihe überträgt.
5. Berechnung
In diesem Schritt multipliziert man die Eingabe-Zahl mit der bekannten Nullstelle (im Bild durch graue Pfeile markiert) und addiert das Ergebnis mit dem nachfolgenden Koeffizienten.
Ist das letzte Resultat 0, so handelt es sich auch wirklich um eine Nullstelle.
Note:
Anhand der Resultat-Reihe im Horner-Schema lässt sich das übrigbleibende Polynom ablesen.Rechnet man die Nullstelle
1aus der Rechnung3x^3 - 15x + 12heraus, so würde das übrigbleibende Polynom folgendermassen lauten:3x^2 + 3x - 12Verdeutlicht:
3x^3 - 15x + 12 = (x - 1) \cdot (3x^2 + 3x - 12)
Stammfunktion
Umkehrung von Ableitungen gemäss der Seite über Ableitungen.
Alle Ableitungsregeln können unter Ableitungen nachgeschlagen werden.
Integrale
Integrale erlauben es, die Fläche unter Funktionen zu berechnen:
Beispiel anhand der Funktion $f(x) = x^3 + 5$
Integrale haben folgende Erscheinungsform:
\int_{a}^{b}{f(x)}dxDie Zeichen haben folgende Bedeutung:
\int: Integrations-Zeichena: Die Untergrenze (Punkt ab dem integriert werden soll)b: Die Obergrenze (Punkt bis zu dem integriert werden soll)f(x): Zu integrierende Funktiondx: Bezeichnet, dassxintegriert wird, indem unendlich kleine Rechtecke aufsummiert werden.
Grundintegrale
$$\begin{aligned}
\int{a}dx &= ax \
\int{x^n}dx &= \frac{x^{n+1}}{n + 1}, &n &\not = -1 \
\int{\frac{1}{x}}dx &= \ln(|x|), &x &\not = 0 \
\int{a^x}dx &= \frac{a^x}{\ln(a)}, &a &> 0, &a &\not = 1
\end{aligned}
Integration von Produkten
Produkte benötigen zum Teil spezielle Vorgehensweisen um sie zu integrieren.
Zwei gängige Wege dazu sind im Folgenden Beschrieben.
Integration durch Substitution
Die Integration durch Substitution basiert auf der folgenden Regel:
\int_a^b{f(u(x)) \cdot u'(x)}dx = \int_{u(a)}^{u(b)}{f(u)}duDie Integration durch Substitution wird hier anhand des folgenden Beispiels gezeigt:
\int_0^{\sqrt{\frac{\pi}{2}}}{\cos(x^2) \cdot x}dx1. Funktionen bestimmen
Im Folgenden werden die Haupt- und die Unterfunktion bestimmt.
u(x) = x^2g(x) = \cos(u) \cdot xf(x) = g(u(x))
2. Substitutions-Gleichung für $dx$
Diese kann mit folgender Regel ermittelt werden:
\frac{du}{dx} = u'(x) \Rightarrow dx = \frac{du}{u'(x)}Das ergibt in diesem Beispiel folgendes:
\frac{du}{dx} = u'(x) = 2x \Rightarrow dx = \frac{du}{2x}3. Substitution
Nun müssen die errechneten Werte in die folgende Formel eingesetzt werden:
\int_{u(a)}^{u(b)}{f(u)}duWobei du durch unser errechnetes dx ersetzt werden muss.
Wichtig ist hierbei, dass sich x komplett wegkürzen lassen muss.
$$\int_0^{\sqrt{\frac{\pi}{2}}}{\cos(x^2) \cdot x}dx =
\int_{u(0)}^{u(\sqrt{\frac{\pi}{2}})}{\cos(u) \cdot x \cdot \frac{du}{2x}}
Vereinfacht ergibt das folgendes:
\int_0^{\frac{\pi}{2}}{\frac{1}{2} \cdot \cos(u)}du = \left[\frac{1}{2} \cdot \sin(u)\right]_0^{\frac{\pi}{2}}4. Resultat berechnen
\left[\frac{1}{2} \cdot \sin(u)\right]_0^{\frac{\pi}{2}} = \left(\frac{1}{2} \cdot 1\right) - \left(\frac{1}{2} \cdot 0\right) = \frac{1}{2}Bei Integralen, die keine Grenzen definiert haben, lässt sich das Ergebnis nicht eindeutig bestimmen.
Hätte das ursprüngliche Integral keine Grenzen, wäre das Ergebnis folgendes:
\left[\frac{1}{2} \cdot \sin(u)\right] = \frac{1}{2} \cdot \sin(u) + C5. Rücksubstitution
Im Falle eines Integrals ohne Grenzen muss die Variable u rück-substituiert werden:
\frac{1}{2} \cdot \sin(u) + C = \frac{1}{2} \cdot \sin(x^2) + CPartielle Integration
Die Partielle Integration beruht auf folgender Regel:
Bestimmt:
\int_a^b{u'(x) \cdot v(x)dx} = \left[u(x) \cdot v(x)\right]_a^b - \int_a^b{u(x) \cdot v'(x)}dxUnbestimmt:
\int{u'(x) \cdot v(x)}dx = u(x) \cdot v(x) - \int{u(x) \cdot v'(x)}dxDie Partielle Integration wird anhand des folgenden Beispiels erklärt:
\int_0^\pi{sin(x) \cdot x}dxFolgende Schritte müssen für die partielle Integration durchgeführt werden:
1. Unterfunktionen bestimmen
Einem Teil der Funktion v und einem anderen u' zuordnen. Sollte die partielle Integration nicht funktionieren, kann in diesem Schritt die Zuordnung von v und u' vertauscht werden.
u'(x) = sin(x)v(x) = x
2. Stammfunktion von u' und Ableitung von v bestimmen
u(x) = -\cos(x)v'(x) = 1
3. Resultat berechnen
Daraus ergibt sich folgende Gleichung:
\int_0^\pi{u'(x) \cdot v(x)dx} = \left[u(x) \cdot v(x)\right]_0^\pi - \int_0^\pi{u(x) \cdot v'(x)}dx\left[-\cos(x) \cdot x\right]_0^\pi - \int_0^\pi{-\cos(x) \cdot 1}dx((1 \cdot \pi) - (1 \cdot 0)) - \int_0^\pi{-\cos(x)}dx(\pi - 0) - \left[\sin(x)\right]_0^\pi(\pi - 0) - (\sin(0) - \sin(\pi))(\pi - 0) - (0 - 0) = \piNote:
Die Partielle Integration kann auch für einfache Operationen verwendet werden, indem eine Multiplikation mit1durchgeführt wird.Beispiel:
\int{ln(x)}dx = \int{ln(x) \cdot 1}dx
Partialbruchzerlegung
Für die Partialbruchzerlegung muss der zu integrierende Bruch vollständig gekürzt sein.
Die Partialbruchzerlegung wird anhand der folgenden Aufgabe erklärt:
\int{\frac{x + 1}{x^3 + 5x^2 + 8x - 4}}dxFolgende Schritte müssen durchgeführt werden:
1. Nullstellen des Nenners bestimmen
Durch erraten: (Eine der Nullstellen ist 1)
Linearfaktor abspalten mit Horner-Schema:
Verbleibendes Polynom: x^2 - 4x + 4 = (x - 2) \cdot (x - 2)
Die verbleibende, doppelte Nullstelle ist also x = 2.
2. Jeder Nullstelle eine Summe von Nullstellen zuordnen
- Für einfache Nullstellen:
\rightarrow \frac{A}{x - x_1} - Für doppelte Nullstellen:
\rightarrow \frac{A_1}{x - x_1} + \frac{A_2}{(x - x_1)^2} - Für $r$-fache Nullstellen:
\rightarrow \frac{A_1}{x - x_1} + \frac{A_2}{(x - x_1)^2} + ... + \frac{A_r}{(x - x_1)^r}
Das ergibt im Fall des Beispiels folgendes:
\frac{x + 1}{x^3 - 5x^2 + 8x - 4} = \frac{A}{x - 1} + \frac{B}{x - 2} + \frac{C}{(x - 2)^2}3. Brüche gleichnamig machen
\frac{x + 1}{(x - 1)(x - 2)^2} = \frac{A(x - 2)^2}{(x + 1)(x - 2)^2} + \frac{B(x - 1)(x - 2)}{(x + 1)(x - 2)^2} + \frac{C(x - 1)}{(x + 1)(x - 2)^2}Da die Brüche nun gleichnamig sind, können sämtliche Nenner weggekürzt werden:
x + 1 = A(x - 2)^2 + B(x - 1)(x - 2) + C(x - 1)4. Koeffizienten mit Hilfe von LGS ausrechnen
Gleichung ausmultiplizieren und nach Potenz zerlegen:
(A + B)x^2 + (C - 4A - 3B)x + (4A + 2B - C)x + 1beinhaltet keinx^2. Also muss(A + B)zwingend0ergeben:A + B = 0x + 1beinhaltet1x. Also mussC - 4A - 3B1ergeben:C - 4A - 3B = 1x + 1beinhaltet eine Konstante1. Also muss4A + 2B - C1ergeben:4A + 2B - C = 1
Das Lösen des Gleichungssystems ergibt folgende Resultate:
A = 2B = -2C = 3
Daraus ergibt sich folgendes:
\frac{x + 1}{(x - 1)(x - 2)^2} = \frac{2}{x - 1} + \frac{-2}{x - 2} + \frac{3}{(x - 2)^2}5. Integration der Teilbrüche
Für Nenner ohne Exponent:
\int{\frac{1}{x - x_0}}dx = \int{\frac{1}{u}}du = \ln(|u|) + c = \ln(|x - x_0|) + cFür Nenner mit Exponent:
$$\begin{split}
\int{\frac{1}{(x - x_0)^r}}dx = \int{u^{-r}}du & = \frac{u^{-r + 1}}{-r + 1} + c \
& = \frac{(x - x_0)^{-r + 1}}{1 - r} + c \
& = \frac{1}{(1 - r)(x - x_o)^{r - 1}} + c
\end{split}
Für das aktuelle Beispiel ergibt das folgendes:
$$\begin{split}
\int{\frac{2}{x - 1} + \frac{2}{x - 2} + \frac{3}{(x - 2)^2}}dx & = \int{\frac{2}{x - 1}} - \int{\frac{2}{x - 2}} - \int{\frac{3}{(x - 1)^2}} \
& = 2 \cdot \int{\frac{1}{x - 1} - 2 \cdot \int{\frac{1}{x - 2}}} - 3 \cdot \int{\frac{1}{(x - 2)^2}} \
& = 2 \cdot \ln(|x - 1|) - 2 \cdot \ln(|x - 2|) - 3 \cdot \frac{1}{x - 2} + c
\end{split}
Leitfaden
Uneigentliche Integrale
Uneigentliche Integrale sind Integrale, welche einen unendlich grossen Integrationsbereich hat oder eine Polstelle (Grenze an unendlichem Wert) enthält.
Uneigentlicher Integrationsbereich
Dies ist der Fall, wenn die Untergrenze eines Integrals -\infin oder dessen Obergrenze +\infin ist.
Beispiel anhand des Integrals $\int_1^{\infin} 6 \cdot \frac{1}{x^2}$
Uneigentliche Integrale können berechnet werden, indem man erst die Stammfunktion ausformuliert, um dann den Grenzwert zu berechnen.
1. Bestimmung der Stammfunktion
\int_1^{\infin}{6 \cdot \frac{1}{x^2}} = \left[6 \cdot -\frac{1}{x}\right]_1^{\infin}2. Grenzwert mit Hilfe von \lim berechnen
\left[6 \cdot -\frac{1}{x}\right]_1^{\infin} = 6 \cdot -\frac{1}{\infin} - 6 \cdot -\frac{1}{1} = 6 \cdot 0 - -6 \cdot -1 = 6Regel Bernoulli de l'Hopital
Wenn für eine Funktion f(x) und g(x) folgendes gilt:
f(x)undg(x)sind in der Umgebung vonx_0berechenbar.\frac{f(x)}{g(x)}ergibt, wennx \rightarrow x_0\frac{0}{0}oder\frac{\infin}{\infin}
Dann gilt:
\lim_{x \rightarrow x_0}{\frac{f(x)}{g(x)}} = \lim_{x \rightarrow x_0}{\frac{f'(x)}{g'(x)}}Differentialgleichungen
Gewöhnliche Differentialgleichungen
Differentialgleichungen sind Funktionen, welche als Rückgabewert an Stelle eines Skalar-Werts eine Funktion liefert.
Eine Differentialfunktion wird dargestellt durch die Ableitung, die resultierende Funktionen haben sollen:
So sind für die Differenzialgleichung y' = x - y + 1 alle resultierende Funktionen gültig, welche die Ableitung x - y + 1 haben.
Die Ordnung einer Differentialgleichung sagt aus, was der höchste Ordnung der höchsten vorkommenden Ableitung.
Differentialgleichungen 1. Ordnung
Differentialgleichungen 1. Ordnung lassen sich als Richtungsfelder darstellen:
Obig zu sehen ist das Richtungsfeld für die Differentialgleichung y' = x - y + 1.
Die Striche zeigen jeweils die Steigung, die das Resultate der Differentialgleichung mit dem entsprechenden $x$- und $y$-Wert hat.
Hierbei steht 0 für keine Steigung (waagerecht), -1 für eine 45°-Senkung nach unten und 1 für eine 45°-Steigung nach oben.
Alternativ lässt sich die Differentialgleichung auch in tabellarischer Form für y' darstellen:
f'(x_0, y_0) |
x_0 = -3 |
x_0 = -2 |
x_0 = -1 |
x_0 = 0 |
x_0 = 1 |
x_0 = 2 |
x_0 = 3 |
|---|---|---|---|---|---|---|---|
y_0 = 2 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
y_0 = 1 |
-3 |
$-2 | -1 |
0 |
1 |
2 |
3 |
y_0 = 0 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
y_0 = -1 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
y_0 = -2 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
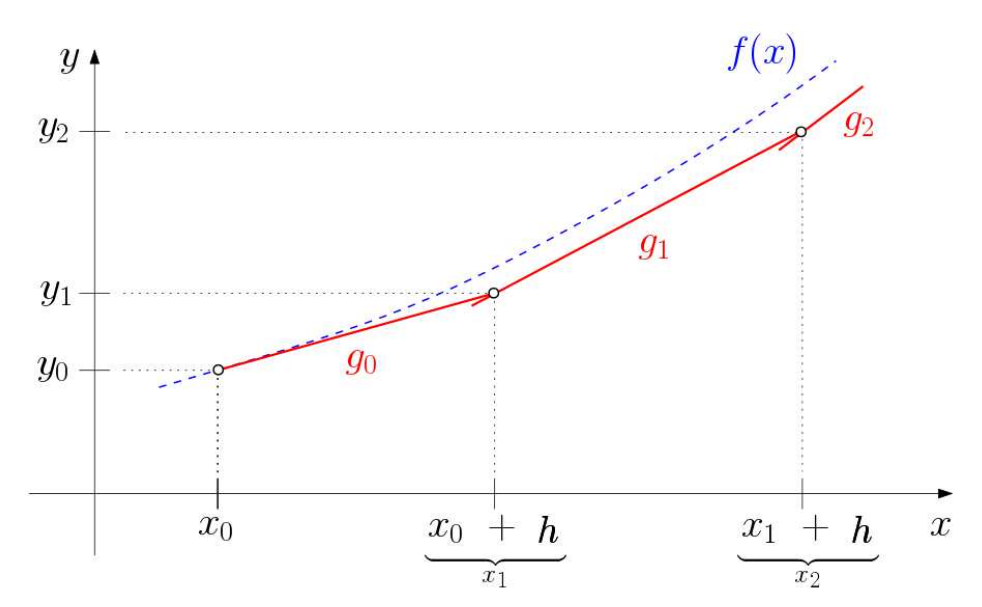
Euler-Schritte
Ein Weg, um eine Lösung für eine Differentialgleichung zu approximieren ist die Methode der Euler-Schritte.
Beispiel mit folgenden Parametern:
y' = x + y, x_0 = 0, y_0 = 1, h = 1
| Steigung Gerade | Berechnung | Beispiel |
|---|---|---|
g_0\text{: } m_0 = F(x_0, y_0) = x_0 + y_0 |
x_1 = x_0 + h |
= 0 + 1 = 1 |
Im Beispiel: 1 |
y_1 = y_0 + h \cdot F(x_0, y_0) |
= 1 + 1 \cdot (0 + 1) = 2 |
g_1\text{: } m_1 = F(x_1, y_1) = x_1 + y_1 |
x_1 = x_0 + h |
= 1 + 1 = 2 |
Im Beispiel: 3 |
y_1 = y_0 + h \cdot F(x_1, y_1) |
= 2 + 1 \cdot (1 + 2) = 5 |
g_2\text{: } m_2 = F(x_2, y_2) = x_2 + y_2 |
x_3 = x_2 + h |
= 2 + 1 = 3 |
Im Beispiel: 7 |
y_3 = y_2 + h \cdot F(x_2, y_2) |
= 5 + 1 \cdot (2 + 5) = 12 |
| etc. | etc. | etc. |
Den Abstand zwischen den einzelnen Euler-Schritte h kann hierbei frei gewählt werden. Je kleiner h gewählt wird, desto genauer wird das Resultat.
Separierbare Differentialgleichungen
Definition
Eine Differentialgleichung 1. Ordnung ist _separierbar-, wenn sie sich in folgende Form bringen lässt:
y' = f(x) \cdot g(y)Beispiele
y' = (x^2 + \sin(x)) \cdot (e^y - y + 7)ist separierbary' = x - y + 1ist nicht separierbar
Lösungsweg
- Gleichung zu Differentialquotient umschreiben:
y' = \frac{dy}{dx} = f(x) \cdot g(y) - Trennung der Variablen:
\frac{dy}{g(y)} = f(x) \cdot dx - Integration auf beiden Seiten der Gleichung:
\int{\frac{dy}{g(y)} = \int{f(x) \cdot dx}} - Auflösen nach
y
Beispiel
y' = k \cdot y1. Gleichung zu Differentialquotient umschreiben:
y' = \frac{dy}{dx} = \underbrace{k}_{f(x)} \cdot \underbrace{y}_{g(y)}2. Trennung der Variablen:
Alle x und y auf separate Seite des = bringen:
\frac{dy}{y} = k \cdot dx3. Integration auf beiden Seiten der Gleichung:
$$\int{\frac{dy}{y}} = \int{\frac{1}{y}}dy = \ln(|y|) \ \int{k \cdot dx} = k \cdot x + C \ \ln(|y|) = k \cdot x + C$$
4. Auflösen nach y:
$$\ln(|y|) = k \cdot x + C \
|y| = e^{k \cdot x + C} \
y = \pm e^{k \cdot x + C} = \underbrace{\pm e^C}_{a} \cdot e^{k \cdot x} = a \cdot e^{k \cdot x}
Kontrolle:
$$y' = (a \cdot e^{k \cdot x})' = a \cdot k \cdot e^{k \cdot x} \ k \cdot y = k \cdot a \cdot e^{k \cdot x} \ y' = k \cdot y$$
Autonome Differentialgleichung
Als autonom werden die Differentialgleichungen bezeichnet, die sich in folgende Form bringen lassen:
y' = f(y)Beispiele
| Gleichung | Autonom? |
|---|---|
y' = y^2 + 6 |
Ja |
y' = x + y |
Nein |
y' = \frac{y}{x} |
Nein |
y' = y^2 \cdot \sqrt{1 - \sin(y)} - \ln(y) |
Ja |
Lösungsweg
Gleich wie separierbare Differentialgleichungen.
Lineare Differentialgleichung 1. Ordnung
Eine Differentialgleichung 1. Ordnung ist lineare, wenn sie sich in folgende Form bringen lässt:
y' = f(x) \cdot y + g(x)g(x) wird hierbei als Störglied oder Störfunktion bezeichnet.
Solche Differentialgleichungen nennen sich "linear", weil sowohl y als auch y' keinen Exponenten haben. Es spielt es keine Rolle, ob x in f(x) oder g(x) eine Potenz hat.
Eine lineare Differentialgleichung 1. Ordnung ist dann homogen, wenn g(x) 0 entspricht. In allen anderen Fällen ist die Differentialgleichung inhomogen.
Lösungswege
Lösung durch Variabel-Separierung
Beispiel anhand folgender Formel:
y' = \frac{2y}{x} + x^31. Komponenten der linearen Differentialgleichung bestimmen:
$$\begin{align*}
f(x) &= \frac{2}{x} \
g(x) &= x^3
\end{align*}
2. Homogenen Anteil berechnen:
In diesem Schritt wird die Differentialgleichung ohne $g(x)$ berechnet.
Dies funktioniert mit Hilfe der Variabel-Trennung nach folgender Formel:
y_h = C \cdot e^{\int{f(x)}dx}Für das Beispiel ergibt das folgendes:
y_h = C \cdot e^{\int{\frac{2}{x}}} = C \cdot e^{2 \cdot \ln(|x|)} = C \cdot e^{\ln(|x|^2)} = C \cdot e^{\ln(x^2)} = C \cdot x^23. Partikulären Anteil berechnen:
Mit Hilfe der folgenden Formel kann der Partikuläre Anteil berechnet werden:
y_P = y_h \cdot \int{\frac{g(x)}{y_h}}dxFür das Beispiel ergibt das wiederum:
y_P = C \cdot x^2 \cdot \int{\frac{x^3}{C \cdot x^2}}dx = x^2 \cdot \int{x} = x^2 \cdot \frac{x^2}{2} = \frac{x^4}{2}4. Homogenen und Partikulären Anteil addieren:
y = y_h + y_P = C \cdot x^2 + \frac{x^4}{2}Lösung durch Variation der Konstanten
Eine weitere Möglichkeit ist das Verfahren "Variation der Konstanten".
Folgend ein Beispiel anhand folgender Differentialgleichung:
y' = \cos(x) - \frac{y}{x}\text{ für x > 0}1. Komponenten bestimmen:
$$\begin{align*}
f(x) &= -\frac{1}{x} \
g(x) &= \cos(x) \
F(x) &= -\ln(x)\text{ für x > 0}
\end{align*}
2. Homogene Gleichung berechnen:
Mit Hilfe folgender Formel lässt sich der homogene Anteil berechnen:
y_0 = C \cdot e^{F(x)}Im aktuellen Beispiel ergibt das folgendes:
y_0 = C \cdot e^{F(x)} = C \cdot e^{-\ln(x)} = \frac{C}{x}3. Konstante C ersetzen
Im nächsten Schritt wird die Konstante C im zuvor berechneten homogenen Anteil durch folgende Formel ersetzt:
K(x) = \int{g(x) \cdot e^{-F(x)}}dxFür das Beispiel ergibt das folgendes:
$$\begin{align*}
\frac{K(x)}{x} \
&= \frac{1}{x} \cdot \int{g(x) \cdot e^{-F(x)}}dx \
&= \frac{1}{x} \cdot \int{\cos(x) \cdot e^{\ln(x)}}dx \
&= \frac{1}{x} \cdot \int{\cos(x) \cdot x}dx \
&= \frac{1}{x} \cdot (\sin(x) \cdot x + \cos(x)) \
&= \frac{\sin(x) \cdot x + \cos(x)}{x}
\end{align*}
Anwendung der Integralrechnung
Der Mittelwert
Der Mittelwert einer Funktion errechnet sich mit der folgenden Formel:
\mu = \frac{1}{b - a} \cdot \int_a^b{f(x)}dxDie Arbeit
\int_{s_1}^{s_2}{F(s)}dsRotationskörper
Rotationskörper um die $x$-Achse
V = \pi \cdot \int_a^b{(f(x))^2}dxRotationskörper um die $y$-Achse
V = \pi \cdot \int_c^d{(g(y))^2}dyMantelfläche eines Rotationskörpers
M = 2 \cdot \pi \cdot \int_a^b{y \cdot \sqrt{1 + (y')^2}}dxBogenlänge einer Kurve
s = \int_a^b{\sqrt{1 + (y')^2}}dxSchwerpunkt
x_S = \frac{1}{A} \cdot \int_a^b{x \cdot (f_o(x) - f_u(x))}dxy_S = \frac{1}{2A} \cdot \int_a^b{(f_o^2(x) - f_u^2(x))}dxSchwerpunkt eines Rotationskörpers
x_S = \frac{\pi}{V} \cdot \int_a^b{x \cdot f^2(x)}dxy_S = 0z_S = 0Taylor-Reihen
Herleitung
Polynom durch Stützpunkte Legen
Um ein Polynom auf n Stützpunkte zu legen, muss das Polynom vom Grad n - 1 sein.
Mit Hilfe eines Gleichungssystems lässt sich bestimmen, durch welche bestimmte Stützpunkte durchquert.
Beispiel
Der Vorgang wird anhand der Gleichung f(x) = e^{2x} aufgezeigt.
1. Stützpunkte Identifizieren:
Der Graph f(x) = e^{2x} läuft unter anderem durch die folgenden Stellen:
(0, 1)(1, e^2)(2, e^4)
2. Gleichungssystem aufstellen:
Für 3 Stützpunkte benötigt das Polynom, wie erwähnt, einen Grad von 3.
Ein Polynom 3. Grades hat den folgenden Aufbau:
p(x) = a + bx + cx^2Daraus lässt sich anhand der Stützpunkte folgendes Gleichungssystem aufstellen:
$$\begin{align*}
1 &= a + 0b + 0c \
e^2 &= a + b + c \
e^4 &= a + 2b + 4c \
\end{align*}
Das Lösen dieses Gleichungssystems ergibt folgendes:
$$\begin{align*}
a &= 1 \
b &= e^2 - 1 - c = -14.02 \
c &= \frac{e^4 + 1}{2} - e^2 = 20.41
\end{align*}
Die ergebende Polynomfunktion ist:
p(x) = 1 - 14.02x + 20.41x^2Lokale Approximation
Ziel der lokalen Approximation ist es, eine Annäherung an eine Funktion zu finden, die an einem bestimmten Punkt x_0 besonders genau am Funktionswert f(x_0) liegt.
Dies ist möglich mit der folgenden Formel:
Taylor-Polynom
Für eine Approximation mit einem Taylor-Polynom vom Grad n der Funktion f(x) an der Stelle x_0 kann folgende Formel verwendet werden:
p(x) = \sum_{k = 0}^{n}{\frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k}Taylor-Reihe
Unter Taylor-Reihe versteht man ein unendliches Taylor-Polynom:
t_f(x) = \sum_{k = 0}^\infin{\frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k}Konvergenz
Die Konvergenz beschreibt den Fakt, dass Annäherungen zum Teil mit der anzunähernden Funktion übereinstimmen.
Hierbei steht der Konvergenz-Bereich für die Stellen, an denen die Funktion und die Annäherung übereinstimmen.
Potenzreihen
Grundsätzliche Formel einer Potenzreihe.
P(x) = \sum_{k = 0}^\infin{a_k \cdot (x - x_0)^k}Quotienten-Kriterium:
Für jede PotenzreiheP(x) = \sum_{k = 0}^\infin{a_k \cdot (x - x_0)^x}gibt es einen Abstandr, so dass
- alle
x \in (x_0 - r, x_0 + r)zum Konvergenz-Bereich gehören- alle
x \in (-\infin, x_0 - r) \cup (x_0 + r, \infin)nicht zum Konvergenz-Bereich gehören